「ベッチ数」の版間の差分
リンク貼替え (Wikipedia:Bot作業依頼, oldid=57465452 による) |
改訳 タグ: サイズの大幅な増減 ビジュアルエディター |
||
| 1行目: | 1行目: | ||
{{要改訳}} |
{{要改訳}} |
||
'''ベッチ数''' (Betti numbers) とは[[位相空間]]に対する不変量で自然数に値をもつ。 |
|||
[[File:Torus.png|thumb|alt=A torus.|right|thumb|320px|トーラスはひとつの連結成分(b<sub>0</sub>)を持っていて、二つの円状の穴(b<sub>1</sub>)(ひとつは中心を原点とする円で、もうひとつは、管状になっている中の円状の部分)であり、2-次元の中身のない部分を中に持つ(内部が管状となっている)ものがひとつ(b<sub>2</sub>)であるので、ベッチ数は 1(b<sub>0</sub>), 2(b<sub>1</sub>), 1(b<sub>2</sub>) となる.]] |
[[File:Torus.png|thumb|alt=A torus.|right|thumb|320px|トーラスはひとつの連結成分(b<sub>0</sub>)を持っていて、二つの円状の穴(b<sub>1</sub>)(ひとつは中心を原点とする円で、もうひとつは、管状になっている中の円状の部分)であり、2-次元の中身のない部分を中に持つ(内部が管状となっている)ものがひとつ(b<sub>2</sub>)であるので、ベッチ数は 1(b<sub>0</sub>), 2(b<sub>1</sub>), 1(b<sub>2</sub>) となる.]] |
||
図 |
右の図のようなトーラスを考える。このトーラスに切り口が円周になるように切れ込みをいれたとき、その結果二つのピースに分かれない切り方が、穴のまわりにそって一周する方法と、縦に切断する方法の二通りある。このことからトーラスの 1 次ベッチ数は 2 である<ref>{{cite web|last=Barile, and Weisstein|first=Margherita and Eric|title=Betti number|url=http://mathworld.wolfram.com/BettiNumber.html|publisher=From MathWorld--A Wolfram Web Resource.|accessdate=26 Feb. 2014}}</ref>。直感的な言葉を使うと、ベッチ数は様々な次元の「穴」の数である。例えば、円の 1 次ベッチ数は 1であり、一般的なプレツェル(pretzel)の場合は、1 次ベッチ数は穴の数の 2 倍となる。 |
||
ベッチ数は、今日、数学のみならず[[計算機科学]]や[[デジタル画像]]などの分野でも研究されている。 |
|||
「ベッチ数」ということばは、[[エンリコ・ベッチ]](Enrico Betti)にちなみ、[[アンリ・ポアンカレ]](Henri Poincaré)により命名された。 |
「ベッチ数」ということばは、[[エンリコ・ベッチ]](Enrico Betti)にちなみ、[[アンリ・ポアンカレ]](Henri Poincaré)により命名された。 |
||
<!---In [[algebraic topology]], the '''Betti numbers''' are used to distinguish [[topological space]]s based on the connectivity of n-dimensional [[simplicial complex]]es. |
|||
[[File:Torus.png|thumb|alt=A torus.|A torus has one connected component(b<sub>0</sub>), two circular holes(b<sub>1</sub>,the one in the center and the one in the middle of the "donut"), and one two-dimensional void(b<sub>2</sub>, the inside of the "donut") yielding Betti numbers of 1(b<sub>0</sub>),2(b<sub>1</sub>),1(b<sub>2</sub>).]] |
|||
Each n-th Betti number represents the rank of the n-th [[homology group]], denoted H<sub>n</sub>, which tells us the maximum amount of cuts that can be made before separating a surface into two pieces or 0-cycles, 1-cycles, etc., in the geometric figure.<ref>{{cite web|last=Barile, and Weisstein|first=Margherita and Eric|title=Betti number|url=http://mathworld.wolfram.com/BettiNumber.html|publisher=From MathWorld--A Wolfram Web Resource.}}</ref> These numbers are used today in fields such as [[simplicial homology]], [[computer science]], [[digital images]], etc. |
|||
The term "Betti numbers" was coined by [[Henri Poincaré]] after [[Enrico Betti]].--> |
|||
==定義== |
==定義== |
||
非負の整数を k として、空間 X の k 次ベッチ数 b<sub>k</sub>(X) は、X の k 次[[ホモロジー群]] H<sub>k</sub>(X) の[[アーベル群のランク|ランク]]として定義される。ホモロジー群は[[有理数|有理数体]] '''Q''' 上のベクトル空間とすることもできるので、H<sub>k</sub>(''X''; '''Q''') のベクトル空間の次元としてベッチ数を定義することもできる。[[普遍係数定理]]は、ねじれのない単純な場合には(係数の取り方に依存せず)これらの定義が同じであることを示している。 |
|||
インフォーマルには、k 番目のベッチ数は、非連結な k-次元曲面の数のことを言う.先頭のいくつかのベッチ数は次のように定義される。 |
|||
* b<sub>0</sub> は連結成分の数 |
|||
* b<sub>1</sub> 「円のような」、もしくは 1-次元の穴の数 |
|||
* b<sub>2</sub> 中身のない面でできている 2-次元の穴の数 |
|||
またベッチ数を係数にもつ多項式としてポアンカレ多項式を定義する。すなわち、X のポアンカレ多項式 P<sub>X</sub>(t) とは b<sub>0</sub>(X)+b<sub>1</sub>(X)t+b<sub>2</sub>(X)t<sup>2</sup>+...+b<sub>n</sub>(X)t<sup>n</sup> のことである。 |
|||
2-次元ベッチ数までは、現実の世界は 0, 1, 2, 3-次元であることを見ているので、容易に理解することができるが、次のように高次元のベッチ数を理解しようとすることはより難しくなる。 |
|||
==例== |
|||
=== 単体複体 === |
|||
(正式な一般次元のベッチ数の定義としては、)非負の整数を k として、空間 X の k 次ベッチ数 b<sub>k</sub>(X) は、X の k 次[[ホモロジー群]]である H<sub>k</sub>(X) の[[アーベル群のランク|ランク]]として定義される。この場合のホモロジー群は、[[有理数]]体 '''Q''' 上のベクトル空間である。k 次ホモロジー群は <math> H_{k} = \ker \delta_{k}/\operatorname{im} \delta_{k+1} </math> であり、<math> \delta_{k}s </math> は[[複体|単体的複体]]の境界写像であるので、H<sub>k</sub> のランクは、k次ベッチ数である。同値なことであるが、この場合にはホモロジー群は[[有理数|有理数体]] '''Q''' 上のベクトル空間とすることもできるので、H<sub>k</sub>(''X''; '''Q''') のベクトル空間の次元としてベッチ数を定義することもできる。[[普遍係数定理]]は、ねじれのない単純な場合には(係数の取り方に依存せず)これらの定義が同じであることを示している。 |
|||
[[ファイル:Simplicialexample.png|代替文=Example|800x800ピクセル]] |
|||
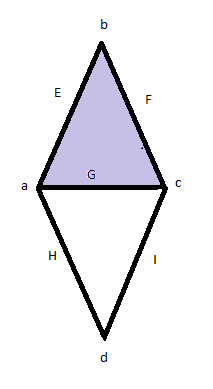
上の図のような[[単体的複体|単体複体]]でのベッチ数を計算する。これは0-単体として a, b, c, d, 1-単体として E, F, G, H, I, 2-単体として色のついた部分 J ただ一つをもつものである。この図の連結成分はただ一つであり、1 次元の穴は色のついてない部分すなわち頂点 a, c, d をもつ三角形の部分である。また平面上にあり、「空洞」をもたない。以上の事からb<sub>0</sub>=1, b<sub>1</sub>=1,b<sub>2</sub>=0 であり、ポアンカレ多項式は 1+t となる。 |
|||
さらに一般的には、[[可換体|体]] F に対して、F に係数を持つ k 次ベッチ数 b<sub>k</sub>(X, F) を、H<sub>k</sub>(X, F) のベクトル空間の次元として定義することができる。 |
|||
<!---==Definition== |
|||
Informally, the ''k''th Betti number refers to the number of ''k''-dimensional holes on a topological surface. The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional [[simplicial complex]]es: |
|||
* b<sub>0</sub> is the number of connected components |
|||
* b<sub>1</sub> is the number of one-dimensional or "circular" holes or tunnels |
|||
* b<sub>2</sub> is the number of two-dimensional "voids" or "cavities" |
|||
The two-dimensional Betti numbers are easily understandable because we see the world in 0, 1, 2, and 3-dimensions, however, the following Betti numbers are difficult to contemplate due to the higher-dimensional understanding. |
|||
=== グラフ理論 === |
|||
For a non-negative [[integer]] ''k'', the ''k''th Betti number ''b''<sub>''k''</sub>(''X'') of the space ''X'' is defined as the [[rank of an abelian group|rank]] (number of generators) of the [[abelian group]] ''H''<sub>''k''</sub>(''X''), the ''k''th [[homology group]] of ''X''. The homology group of k is <math> H_{k} = \frac{ker \delta_{k}}{im \delta_{k+1}} </math>, the <math> \delta_{k}s </math> are the boundary maps of the [[simplicial complex]] and the rank of H<sub>k</sub> is the Betti number for k. Equivalently, one can define it as the [[vector space dimension]] of ''H''<sub>''k''</sub>(''X''; '''Q''') since the homology group in this case is a vector space over '''Q'''. The [[universal coefficient theorem]], is a very simple case, shows that these definitions are the same. |
|||
{{仮リンク|位相的グラフ理論|en|topological graph theory}}では、頂点 n 個、m 本の辺、k 個の連結成分をもったグラフ G の 1次ベッチ数は、次の値に等しい。 |
|||
<math>m - n + k.\ </math> |
|||
More generally, given a [[Field (mathematics)|field]] ''F'' one can define ''b''<sub>''k''</sub>(''X'', ''F''), the ''k''th Betti number with coefficients in ''F'', as the vector space dimension of ''H''<sub>''k''</sub>(''X'', ''F'').--> |
|||
<!-- |
|||
===例1:単体複体 K の 1次ベッチ数=== |
|||
{{仮リンク|単体複体|en|simplicial complex}}(simplicial complex)でベッチ数をどのように計算するのかを、簡単な例でみてみる。 |
|||
[[File:Simplicialexample.png|800x1600px|alt=Example|]] |
|||
<br>この単体複体は、0-単体: a,b,c,d、1-単体: E,F,G,H,I、唯一の 2-単体 J を持っている。J はこの図では隠れた領域である。(b<sub>0</sub>) は連結成分としてはひとつであり、隠れた部分である (b<sub>1</sub>) であるが穴が一つ、「空き(void)」や「空洞(cavities)」のない (b<sub>2</sub>) である。このことは、<math>H_{0}</math> のランクは 1 でり、<math>H_{1}</math> のランクは 1 であり、<math>H_{2}</math> のランクは 0 であることを意味する。この図のベッチ数列は 1,1,0,0,... であり、ポアンカレ多項式は、 |
|||
<math>1 +x</math> |
|||
である。--> |
|||
<!--==Example 1: Betti Numbers of a Simplicial Complex K== |
|||
Let us go through a simple example of how to compute the Betti numbers for a [[simplicial complex]]. |
|||
[[File:Simplicialexample.png|800x1600px|alt=Example]]<br> |
|||
Here we have a [[simplicial complex]] with 0-simplices: a,b,c, and d, |
|||
1-simplices: E,F,G,H and I, and the only 2-simplice is J, which is the shaded region in the figure.<br> |
|||
It is clear that there is one connected component in this figure (b<sub>0</sub>), <br> |
|||
one hole, which is the shaded region (b<sub>1</sub>) and no "voids" or "cavities" (b<sub>2</sub>).<br> |
|||
This means that the rank of <math>H_{0}</math> is 1, the rank of <math>H_{1}</math> is 1 and the rank of <math>H_{2}</math> is 0.<br> |
|||
The Betti number sequence for this figure is 1,1,0,0,...; |
|||
the Poincaré polynomial is |
|||
<math>1 +x \,</math>--> |
|||
このことは、辺の数についての[[数学的帰納法]]により直接証明ができる。つまり、新しい辺 1-サイクル分の数を増やすが、もしくは辺の連結成分の数を一つ減らすかのどちらかである。 |
|||
==例2:グラフ理論のベッチ数== |
|||
{{仮リンク|位相的グラフ理論|en|topological graph theory}}では、頂点 n 個、m 本の辺、k 個の連結成分をもったグラフ G の 1次ベッチ数は、次の値に等しい。 |
|||
:<math>m - n + k.\ </math> |
|||
このことは、辺の数についての[[数学的帰納法]]により直接証明ができるかも知れない。つまり、新しい辺 1-サイクル分の数を増やすが、もしくは辺の連結成分の数を一つ減らすかのどちらかである。 |
|||
第一ベッチ数は、[[グスタフ・キルヒホフ]](Gustav Kirchhoff)がベッチ(Betti)の論文以前に導入した用語である{{仮リンク|回路ランク|label=サイクロマチック数|en|Circuit rank}}(cyclomatic number)とも呼ばれる。<ref name="Kotiuga2010">{{cite book|author=Peter Robert Kotiuga|title=A Celebration of the Mathematical Legacy of Raoul Bott|url=http://books.google.com/books?id=mqLXi0FRIZwC&pg=PA20|year=2010|publisher=American Mathematical Soc.|isbn=978-0-8218-8381-5|page=20}}</ref>第一ベッチ数の[[ソフトウェア工学]]への応用は、[[循環的複雑度]]を参照のこと。 |
第一ベッチ数は、[[グスタフ・キルヒホフ]](Gustav Kirchhoff)がベッチ(Betti)の論文以前に導入した用語である{{仮リンク|回路ランク|label=サイクロマチック数|en|Circuit rank}}(cyclomatic number)とも呼ばれる。<ref name="Kotiuga2010">{{cite book|author=Peter Robert Kotiuga|title=A Celebration of the Mathematical Legacy of Raoul Bott|url=http://books.google.com/books?id=mqLXi0FRIZwC&pg=PA20|year=2010|publisher=American Mathematical Soc.|isbn=978-0-8218-8381-5|page=20}}</ref>第一ベッチ数の[[ソフトウェア工学]]への応用は、[[循環的複雑度]]を参照のこと。 |
||
グラフの第 0 番めのベッチ数は、連結成分の数 k を単純に意味している。<ref name="Hage1996">{{cite book|author=Per Hage|title=Island Networks: Communication, Kinship, and Classification Structures in Oceania|url=http://books.google.com/books?id=ZBdLknuP0BYC&pg=PA49|year=1996|publisher=Cambridge University Press|isbn=978-0-521-55232-5|page=49}}</ref> |
グラフの第 0 番めのベッチ数は、連結成分の数 k を単純に意味している。<ref name="Hage1996">{{cite book|author=Per Hage|title=Island Networks: Communication, Kinship, and Classification Structures in Oceania|url=http://books.google.com/books?id=ZBdLknuP0BYC&pg=PA49|year=1996|publisher=Cambridge University Press|isbn=978-0-521-55232-5|page=49}}</ref> |
||
<!--==Example 2: the first Betti number in graph theory== |
|||
In [[topological graph theory]] the first Betti number of a graph ''G'' with ''n'' vertices, ''m'' edges and ''k'' [[Connected component (graph theory)|connected component]]s equals |
|||
=== ポアンカレ多項式の計算例 === |
|||
:<math>m - n + k.\ </math> |
|||
This may be proved straightforwardly by [[mathematical induction]] on the number of edges. A new edge either increments the number of 1-cycles or decrements the number of connected components. |
|||
The first Betti number is also called the [[cyclomatic number]]—a term introduced by [[Gustav Kirchhoff]] before Betti's paper.<ref name="Kotiuga2010">{{cite book|author=Peter Robert Kotiuga|title=A Celebration of the Mathematical Legacy of Raoul Bott|url=http://books.google.com/books?id=mqLXi0FRIZwC&pg=PA20|year=2010|publisher=American Mathematical Soc.|isbn=978-0-8218-8381-5|page=20}}</ref> See [[cyclomatic complexity]] for an application to [[software engineering]]. |
|||
The "zero-th" Betti number of a graph is simply the number of connected components ''k''.<ref name="Hage1996">{{cite book|author=Per Hage|title=Island Networks: Communication, Kinship, and Classification Structures in Oceania|url=http://books.google.com/books?id=ZBdLknuP0BYC&pg=PA49|year=1996|publisher=Cambridge University Press|isbn=978-0-521-55232-5|page=49}}</ref>--> |
|||
==性質== |
|||
(有理)ベッチ数 b<sub>k</sub>(X) は、ホモロジー群の任意の[[ねじれ部分群]](torsion)を考慮に入れてはいないが、しかし、非常に基本的な位相不変量である。直感的な言葉を使うと、ベッチ数は様々な次元の「穴」の数を数えることになる。例えば、円の場合には第一ベッチ数は 1 である。一般的なプレツェル(pretzel)の場合は、第一ベッチ数は穴の数の 2倍となる。 |
|||
有限の単体複体の場合は、ホモロジー群 H<sub>k</sub>(X, '''Z''') は有限生成であり、従って有限ランクである。ホモロジー群は、k が X の単体の一番高い次元を超えている場合は 0 である。 |
|||
有限の CW-複体 K に対し、 |
|||
:<math>\chi(K)=\sum_{i=0}^\infty(-1)^ib_i(K,F), \,</math> |
|||
が成り立つ。ここに <math>\chi(K)</math> は K の[[オイラー標数]]を表し、F は任意の体である。 |
|||
2つの空間 X と Y に対し |
|||
:<math>P_{X\times Y}=P_X P_Y , \, </math> |
|||
が成り立つ。ここに P<sub>X</sub> は X の '''ポアンカレ多項式'''(Poincaré polynomial)(より一般的には、無限次元の空間に対しては{{仮リンク|ポアンカレ級数|en|Poincaré series (modular form)}})、すなわち X のベッチ数の[[母函数]]である |
|||
:<math>P_X(z)=b_0(X)+b_1(X)z+b_2(X)z^2+\cdots , \,\!</math> |
|||
である。{{仮リンク|キネットの定理|en|Künneth theorem}}(Künneth theorem)を参照。 |
|||
X を n-次元多様体とすると、任意の k に対し k と n − k を入れ替える対称性 |
|||
:<math>b_k(X)=b_{n-k}(X) , \,\!</math> |
|||
がある。この時の条件は(閉であること、向き付け可能である多様体であること)である。[[ポアンカレ双対性]]を参照。 |
|||
体 F に依存することは、体の標数に関してだけである。ホモロジー群が[[捩れ (代数)|捩れ]]を持たないとき、ベッチ数は F とは独立となる。[[標数|標数 p]]で、p を素数としたときの p-torsion とベッチ数は、(単純な場合には、[[Tor函手]]を基礎とする)[[普遍係数定理]]により詳細に求められる。 |
|||
<!---==Properties== |
|||
The (rational) Betti numbers ''b''<sub>''k''</sub>(''X'') do not take into account any [[torsion subgroup|torsion]] in the homology groups, but they are very useful basic topological invariants. In the most intuitive terms, they allow one to count the number of ''holes'' of different dimensions. |
|||
For a finite CW-complex ''K'' we have |
|||
:<math>\chi(K)=\sum_{i=0}^\infty(-1)^ib_i(K,F), \,</math> |
|||
where <math>\chi(K)</math> denotes [[Euler characteristic]] of ''K'' and any field ''F''. |
|||
For any two spaces ''X'' and ''Y'' we have |
|||
:<math>P_{X\times Y}=P_X P_Y , \, </math> |
|||
where ''P''<sub>''X''</sub> denotes the '''Poincaré polynomial''' of ''X'', (more generally, the [[Poincaré series (modular form)|Poincaré series]], for infinite-dimensional spaces), i.e. the |
|||
[[generating function]] of the Betti numbers of ''X'': |
|||
:<math>P_X(z)=b_0(X)+b_1(X)z+b_2(X)z^2+\cdots , \,\!</math> |
|||
see [[Künneth theorem]]. |
|||
If ''X'' is ''n''-dimensional manifold, there is symmetry interchanging ''k'' and ''n'' − ''k'', for any ''k'': |
|||
:<math>b_k(X)=b_{n-k}(X) , \,\!</math> |
|||
under conditions (a ''closed'' and ''oriented'' manifold); see [[Poincaré duality]]. |
|||
The dependence on the field ''F'' is only through its [[characteristic (field)|characteristic]]. If the homology groups are [[torsion (algebra)|torsion-free]], the Betti numbers are independent of ''F''. The connection of ''p''-torsion and the Betti number for [[characteristic p|characteristic ''p'']], for ''p'' a prime number, is given in detail by the [[universal coefficient theorem]] (based on [[Tor functor]]s, but in a simple case).--> |
|||
==例== |
|||
#円に対するベッチ数の列は、1, 1, 0, 0, 0, ... |
#円に対するベッチ数の列は、1, 1, 0, 0, 0, ... |
||
#:ポアンカレ多項式は、 |
#:ポアンカレ多項式は、 |
||
| 140行目: | 45行目: | ||
#::<math>(1+x)^n \,</math> ({{仮リンク|キネットの定理|en|Künneth theorem}}により)、ベッチ数は[[二項定理|二項係数]]である。 |
#::<math>(1+x)^n \,</math> ({{仮リンク|キネットの定理|en|Künneth theorem}}により)、ベッチ数は[[二項定理|二項係数]]である。 |
||
無限次元の[[複素射影空間]]のベッチ数の列は、1, 0, 1, 0, 1, ... と周期的となるので、周期の長さは 2 である。この場合は、ポアンカレ函数は多項式ではなく、無限級数 |
|||
この場合は、ポアンカレ函数は多項式ではなく、無限級数 |
|||
:<math>1+x^2+x^4+\dotsb</math> |
:<math>1+x^2+x^4+\dotsb</math> |
||
となる。これは、幾何級数であり、次の有理函数として書き表すことができる。 |
となる。これは、幾何級数であり、次の有理函数として書き表すことができる。 |
||
: <math>\frac{1}{1-x^2}=1+x^2+(x^2)^2+(x^2)^3+\dotsb.</math> |
: <math>\frac{1}{1-x^2}=1+x^2+(x^2)^2+(x^2)^3+\dotsb.</math> |
||
さらに一般的に、任意の周期を持つ数列は、上記のように幾何級数の和として書き表すことができ、例えば、<math>a,b,c,a,b,c,\dots,</math> は母函数 |
|||
:<math>(a+bx+cx^2)/(1-x^3)</math> |
|||
を持つ)、さらに一般的に、[[線型回帰数列|線型再帰数列]]は、[[有理函数]]により生成された数列となる。このようにして、ポアンカレ級数は、有理函数として表されることと、ベッチ数の列が線型再帰数列であることとは同値である。 |
|||
コンパクトな単純リー群のポアンカレ多項式は、 |
コンパクトな単純リー群のポアンカレ多項式は、 |
||
| 170行目: | 70行目: | ||
となる。 |
となる。 |
||
==性質== |
|||
==微分形式の空間の次元との関係== |
|||
(有理)ベッチ数 b<sub>k</sub>(X) は、ホモロジー群の任意の[[ねじれ部分群]](torsion)を考慮に入れてはいないが、しかし、非常に基本的な位相不変量である。 |
|||
<math>X</math> が[[閉多様体]]であるという前提では、ベッチ数の重要さは微分形式から来ることであるかも知れない。すなわち、ベッチ数は[[微分形式#閉形式と完全形式微分形式|閉微分形式]]を[[微分形式#閉形式と完全形式微分形式|完全形式]]で割った剰余空間の次元と考えることができる。上で与えた定義との関係は、3つの基本的な結果である、[[ド・ラームコホモロジー#ド・ラームの定理|ド・ラームの定理]]と[[ポアンカレ双対性]](いつこれが適用されるか)、[[ホモロジー (数学)|ホモロジー論]]の[[普遍係数定理]]を経由して得られる。 |
|||
有限の単体複体の場合は、ホモロジー群 H<sub>k</sub>(X, '''Z''') は全ての k で有限ランクであり、また k が単体の次元を超えている場合は 0 である。 |
|||
<!---In geometric situations when <math>X</math> is a [[closed manifold]], the importance of the Betti numbers may arise from a different direction, namely that they predict the dimensions of vector spaces of [[closed differential form]]s ''[[Modular arithmetic|modulo]]'' [[exact differential form]]s. The connection with the definition given above is via three basic results, [[de Rham's theorem]] and [[Poincaré duality]] (when those apply), and the [[universal coefficient theorem]] of [[homology theory]]. --> |
|||
有限の CW-複体 K に対し、 |
|||
別な見方もできる。つまり、ベッチ数は[[調和形式]]の空間の次数を与えるものと見ることもできる。これには、[[ラプラス作用素|ホッジラプラシアン]]に関する[[ホッジ理論]]の結果をいくつか使う必要がある。 |
|||
:<math>\chi(K)=\sum_{i=0}^\infty(-1)^ib_i(K,F), \,</math> |
|||
この設定で、[[モース理論]]は、ベッチ数の交代和の不等式の組を、与えられた指数の[[モース函数]]の臨界点([[:en:critical point (mathematics)|critical point]]) <math>N_i</math> の数の対応する交代和の項で表す。 |
|||
:<math> b_i(X) - b_{i-1} (X) + \cdots \le N _i - N_{i-1} + \cdots. </math> |
|||
が成り立つ。ここに <math>\chi(K)</math> は K の[[オイラー標数]]を表し、F は任意の体である。 |
|||
[[エドワード・ウィッテン|ウィッテン]]は、モース函数を使いこれらの不等式の説明をして、[[ド・ラームコホモロジー#定義|ド・ラーム複体]]の[[微分形式#外微分|外微分]]を変形した。<ref>Witten, Edward (1982). ''Supersymmetry and Morse theory.'' J. Differential Geom. 17 (1982), no. 4, 661–692.</ref> |
|||
<!---There is an alternate reading, namely that the Betti numbers give the dimensions of spaces of [[harmonic form]]s. This requires also the use of some of the results of [[Hodge theory]], about the [[Hodge Laplacian]]. |
|||
2つの空間 X と Y に対し |
|||
In this setting, [[Morse theory]] gives a set of inequalities for alternating sums of Betti numbers in terms of a corresponding alternating sum of the number of [[critical point (mathematics)|critical points]] <math>N_i</math> of a [[Morse function]] of a given [[Morse theory|index]]: |
|||
:<math> |
:<math>P_{X\times Y}=P_X P_Y , \, </math> |
||
が成り立つ。ここに P<sub>X</sub> は X の '''ポアンカレ多項式'''(Poincaré polynomial)(より一般的には、無限次元の空間に対しては{{仮リンク|ポアンカレ級数|en|Poincaré series (modular form)}})、すなわち X のベッチ数の[[母函数]]である |
|||
:<math>P_X(z)=b_0(X)+b_1(X)z+b_2(X)z^2+\cdots , \,\!</math> |
|||
である。{{仮リンク|キネットの定理|en|Künneth theorem}}(Künneth theorem)を参照。 |
|||
X を向き付け可能な閉多様体で n 次元とすると、任意の k に対し k と n − k を入れ替える[[ポアンカレ双対性]] |
|||
[[Edward Witten|Witten]] gave an explanation of these inequalities by using the Morse function to modify the [[exterior derivative]] in the [[de Rham complex]].<ref>Witten, Edward (1982). ''Supersymmetry and Morse theory.'' J. Differential Geom. 17 (1982), no. 4, 661–692.</ref>--> |
|||
:<math>b_k(X)=b_{n-k}(X) , \,\!</math> |
|||
がある。 |
|||
ホモロジー群が[[捩れ (代数)|捩れ]]を持たないとき、ベッチ数は係数体 F によらず決まる。素数 p に対し整数係数ホモロジー群の p-torsion は[[標数|標数 p]] をもつ係数体 F のベッチ数 b<sub>i</sub>(X,F) を用いて(単純な場合には、[[Tor函手]]を基礎とする)[[普遍係数定理]]により詳細に求められる。 |
|||
==微分形式の空間の次元との関係== |
|||
X が[[閉多様体]]のとき、ベッチ数は[[ド・ラームコホモロジー]]の次元をあたえる。[[微分形式#閉形式と完全形式微分形式|閉形式]]の空間を[[微分形式#閉形式と完全形式微分形式|完全形式]]の空間でわった商空間の次元をあたえる。これは[[ド・ラームコホモロジー#ド・ラームの定理|ド・ラームの定理]]と[[ホモロジー (数学)|ホモロジー論]]の[[普遍係数定理]]によりえられる。 |
|||
また X がリーマン多様体であれば、[[ホッジ理論]]によればベッチ数は[[調和形式]]の空間の次数を与えることがわかる。 |
|||
[[モース理論]]によりベッチ数の交代和と、対応する適切な[[モース函数]]の臨界点([[:en:critical point (mathematics)|critical point]])の数 N<sub>i</sub> の交代和に関する不等式が以下のようにあたえられる。 |
|||
:<math> b_i(X) - b_{i-1} (X) + \cdots \le N _i - N_{i-1} + \cdots. </math> |
|||
[[エドワード・ウィッテン|ウィッテン]]は、モース函数を使いこれらの不等式の説明をして、[[ド・ラームコホモロジー#定義|ド・ラーム複体]]の[[微分形式#外微分|外微分]]を変形した。<ref>Witten, Edward (1982). ''Supersymmetry and Morse theory.'' J. Differential Geom. 17 (1982), no. 4, 661–692.</ref> |
|||
==参考文献== |
==参考文献== |
||
<references /> |
<references /> |
||
2016年5月16日 (月) 02:14時点における版
原文と比べた結果、この記事には多数の(または内容の大部分に影響ある)誤訳があることが判明しています。情報の利用には注意してください。 |
ベッチ数 (Betti numbers) とは位相空間に対する不変量で自然数に値をもつ。

右の図のようなトーラスを考える。このトーラスに切り口が円周になるように切れ込みをいれたとき、その結果二つのピースに分かれない切り方が、穴のまわりにそって一周する方法と、縦に切断する方法の二通りある。このことからトーラスの 1 次ベッチ数は 2 である[1]。直感的な言葉を使うと、ベッチ数は様々な次元の「穴」の数である。例えば、円の 1 次ベッチ数は 1であり、一般的なプレツェル(pretzel)の場合は、1 次ベッチ数は穴の数の 2 倍となる。
ベッチ数は、今日、数学のみならず計算機科学やデジタル画像などの分野でも研究されている。
「ベッチ数」ということばは、エンリコ・ベッチ(Enrico Betti)にちなみ、アンリ・ポアンカレ(Henri Poincaré)により命名された。
定義
非負の整数を k として、空間 X の k 次ベッチ数 bk(X) は、X の k 次ホモロジー群 Hk(X) のランクとして定義される。ホモロジー群は有理数体 Q 上のベクトル空間とすることもできるので、Hk(X; Q) のベクトル空間の次元としてベッチ数を定義することもできる。普遍係数定理は、ねじれのない単純な場合には(係数の取り方に依存せず)これらの定義が同じであることを示している。
またベッチ数を係数にもつ多項式としてポアンカレ多項式を定義する。すなわち、X のポアンカレ多項式 PX(t) とは b0(X)+b1(X)t+b2(X)t2+...+bn(X)tn のことである。
例
単体複体
上の図のような単体複体でのベッチ数を計算する。これは0-単体として a, b, c, d, 1-単体として E, F, G, H, I, 2-単体として色のついた部分 J ただ一つをもつものである。この図の連結成分はただ一つであり、1 次元の穴は色のついてない部分すなわち頂点 a, c, d をもつ三角形の部分である。また平面上にあり、「空洞」をもたない。以上の事からb0=1, b1=1,b2=0 であり、ポアンカレ多項式は 1+t となる。
グラフ理論
位相的グラフ理論では、頂点 n 個、m 本の辺、k 個の連結成分をもったグラフ G の 1次ベッチ数は、次の値に等しい。
このことは、辺の数についての数学的帰納法により直接証明ができる。つまり、新しい辺 1-サイクル分の数を増やすが、もしくは辺の連結成分の数を一つ減らすかのどちらかである。
第一ベッチ数は、グスタフ・キルヒホフ(Gustav Kirchhoff)がベッチ(Betti)の論文以前に導入した用語であるサイクロマチック数(cyclomatic number)とも呼ばれる。[2]第一ベッチ数のソフトウェア工学への応用は、循環的複雑度を参照のこと。
グラフの第 0 番めのベッチ数は、連結成分の数 k を単純に意味している。[3]
ポアンカレ多項式の計算例
- 円に対するベッチ数の列は、1, 1, 0, 0, 0, ...
- ポアンカレ多項式は、
- .
- ポアンカレ多項式は、
- 2-トーラスに対するベッチ数の列は 1, 2, 1, 0, 0, 0, ...
- ポアンカレ多項式は、
- .
- ポアンカレ多項式は、
- 3-トーラスに対するベッチ数の列は 1, 3, 3, 1, 0, 0, 0, ...
- ポアンカレ多項式は、
- .
- ポアンカレ多項式は、
- 同様に、n-次元トーラスに対して
無限次元の複素射影空間のベッチ数の列は、1, 0, 1, 0, 1, ... と周期的となるので、周期の長さは 2 である。この場合は、ポアンカレ函数は多項式ではなく、無限級数
となる。これは、幾何級数であり、次の有理函数として書き表すことができる。
コンパクトな単純リー群のポアンカレ多項式は、
となる。
性質
(有理)ベッチ数 bk(X) は、ホモロジー群の任意のねじれ部分群(torsion)を考慮に入れてはいないが、しかし、非常に基本的な位相不変量である。
有限の単体複体の場合は、ホモロジー群 Hk(X, Z) は全ての k で有限ランクであり、また k が単体の次元を超えている場合は 0 である。
有限の CW-複体 K に対し、
が成り立つ。ここに は K のオイラー標数を表し、F は任意の体である。
2つの空間 X と Y に対し
が成り立つ。ここに PX は X の ポアンカレ多項式(Poincaré polynomial)(より一般的には、無限次元の空間に対してはポアンカレ級数)、すなわち X のベッチ数の母函数である
である。キネットの定理(Künneth theorem)を参照。
X を向き付け可能な閉多様体で n 次元とすると、任意の k に対し k と n − k を入れ替えるポアンカレ双対性
がある。
ホモロジー群が捩れを持たないとき、ベッチ数は係数体 F によらず決まる。素数 p に対し整数係数ホモロジー群の p-torsion は標数 p をもつ係数体 F のベッチ数 bi(X,F) を用いて(単純な場合には、Tor函手を基礎とする)普遍係数定理により詳細に求められる。
微分形式の空間の次元との関係
X が閉多様体のとき、ベッチ数はド・ラームコホモロジーの次元をあたえる。閉形式の空間を完全形式の空間でわった商空間の次元をあたえる。これはド・ラームの定理とホモロジー論の普遍係数定理によりえられる。 また X がリーマン多様体であれば、ホッジ理論によればベッチ数は調和形式の空間の次数を与えることがわかる。
モース理論によりベッチ数の交代和と、対応する適切なモース函数の臨界点(critical point)の数 Ni の交代和に関する不等式が以下のようにあたえられる。
ウィッテンは、モース函数を使いこれらの不等式の説明をして、ド・ラーム複体の外微分を変形した。[4]
参考文献
- ^ Barile, and Weisstein, Margherita and Eric. “Betti number”. From MathWorld--A Wolfram Web Resource.. 26 Feb. 2014閲覧。
- ^ Peter Robert Kotiuga (2010). A Celebration of the Mathematical Legacy of Raoul Bott. American Mathematical Soc.. p. 20. ISBN 978-0-8218-8381-5
- ^ Per Hage (1996). Island Networks: Communication, Kinship, and Classification Structures in Oceania. Cambridge University Press. p. 49. ISBN 978-0-521-55232-5
- ^ Witten, Edward (1982). Supersymmetry and Morse theory. J. Differential Geom. 17 (1982), no. 4, 661–692.
- Warner, Frank Wilson (1983), Foundations of differentiable manifolds and Lie groups, New York: Springer, ISBN 0-387-90894-3.
- Roe, John (1998), Elliptic Operators, Topology, and Asymptotic Methods, Research Notes in Mathematics Series, 395 (Second ed.), Boca Raton, FL: Chapman and Hall, ISBN 0-582-32502-1.