出典: フリー百科事典『ウィキペディア(Wikipedia)』
この項目では、ガンマ関数の対数微分で定義されるポリガンマ関数(polygamma function)について説明しています。E. Barnesによって導入された多重ガンマ関数(multiple gamma function)については「多重ガンマ関数 」をご覧ください。
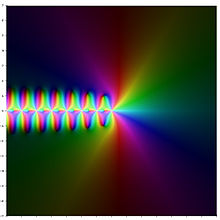
実数x に対するψ(n) (x )の挙動。 オレンジがディガンマ関数、黄色がトリガンマ関数、緑がテトラガンマ関数、赤がペンタガンマ関数、青がヘキサガンマ関数に対応する。 複素平面上でのディガンマ関数ψ(z) 複素平面上でのトリガンマ関数ψ(1) (z) 複素平面上でのテトラガンマ関数ψ(2) (z) 複素平面上でのペンタガンマ関数ψ(3) (z) 数学において、ポリガンマ関数 (ぽりがんまかんすう、英 : polygamma function )とは、ガンマ関数 の対数微分 による導関数 として定義される特殊関数 。ディガンマ関数 やトリガンマ関数 (英語版 )
ガンマ関数 Γ(z ) に対し、その対数微分
ψ
(
n
)
(
z
)
=
d
n
+
1
d
z
n
+
1
ln
Γ
(
z
)
=
d
n
d
z
n
ψ
(
z
)
{\displaystyle \psi ^{(n)}(z)={\frac {d^{n+1}}{dz^{n+1}}}\ln {\Gamma (z)}={\frac {d^{n}}{dz^{n}}}\psi (z)}
で、定義される関数をポリガンマ関数 と呼ぶ。
ψ(z ), ψ(1) (z ), ψ(2) (z ), ψ(3) (z ), ψ(4) (z ) は、それぞれディ -、トリ -、テトラ -、ペンタ -、ヘキサ -ガンマ関数 と呼ばれる。
ポリガンマ関数 ψ(n ) (z ) は z = 0, −1, −2, ... で n + 1 位の極 をもち,それらの点を除く全複素平面 では解析的 になる。
ポリガンマ関数は次の漸化式 を満たす。
ψ
(
n
)
(
z
+
1
)
=
ψ
(
n
)
(
z
)
+
(
−
1
)
n
n
!
z
n
+
1
{\displaystyle \psi ^{(n)}(z+1)=\psi ^{(n)}(z)+{\frac {(-1)^{n}n!}{z^{n+1}}}}
ポリガンマ関数はz ≠0, -1, -2, -3...で次の級数 表示を持つ。
ψ
(
z
)
=
−
γ
−
∑
n
=
0
∞
(
1
z
+
n
−
1
n
+
1
)
{\displaystyle \psi (z)=-\gamma -\sum _{n=0}^{\infty }{\biggl (}{\frac {1}{z+n}}-{\frac {1}{n+1}}{\biggr )}}
ψ
(
n
)
(
z
)
=
(
−
1
)
n
+
1
n
!
∑
k
=
0
∞
1
(
z
+
k
)
n
+
1
(
n
=
1
,
2
,
3
,
⋯
)
{\displaystyle \psi ^{(n)}(z)=(-1)^{n+1}n!\sum _{k=0}^{\infty }{\frac {1}{(z+k)^{n+1}}}\qquad (n=1,2,3,\cdots )}
また、z =0でのテイラー展開 により、|z |<1の領域で次のように表される。
ψ
(
z
+
1
)
=
−
γ
+
∑
k
=
2
∞
(
−
1
)
k
ζ
(
k
)
z
k
−
1
{\displaystyle \psi (z+1)=-\gamma +\sum _{k=2}^{\infty }(-1)^{k}\zeta (k)z^{k-1}}
ψ
(
n
)
(
z
+
1
)
=
(
−
1
)
n
+
1
∑
k
=
1
∞
(
−
1
)
k
−
1
(
n
+
k
−
1
)
!
ζ
(
n
+
k
)
z
k
−
1
(
k
−
1
)
!
(
n
=
1
,
2
,
3
,
⋯
)
{\displaystyle \psi ^{(n)}(z+1)=(-1)^{n+1}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}(n+k-1)!\zeta (n+k)z^{k-1}}{(k-1)!}}\qquad (n=1,2,3,\cdots )}
但し、γ =0.5772...はオイラーの定数 、ζ (n )はリーマンゼータ関数 を表す。
Rez >0のとき、ポリガンマ関数は次の積分表示を持つ。
ψ
(
z
)
=
−
γ
+
∫
0
∞
e
−
t
−
e
−
z
t
1
−
e
−
t
d
t
{\displaystyle \psi (z)=-\gamma +\int _{0}^{\infty }{\frac {e^{-t}-e^{-zt}}{1-e^{-t}}}dt}
ψ
(
n
)
(
z
)
=
(
−
1
)
n
+
1
∫
0
∞
t
n
e
−
z
t
1
−
e
−
t
d
t
(
n
=
1
,
2
,
⋯
)
{\displaystyle \psi ^{(n)}(z)=(-1)^{n+1}\int _{0}^{\infty }{\frac {t^{n}e^{-zt}}{1-e^{-t}}}dt\quad (n=1,2,\cdots )}
ガンマ関数の相反公式に対し、対数微分をとることで次の関係式が導かれる。
(
−
1
)
n
ψ
(
n
)
(
1
−
z
)
−
ψ
(
n
)
(
z
)
=
π
d
n
d
z
n
cot
π
z
{\displaystyle (-1)^{n}\psi ^{(n)}(1-z)-\psi ^{(n)}(z)=\pi {\frac {d^{n}}{dz^{n}}}\operatorname {cot} \pi z}
但し、cot πz は余接関数 を表す。
z →∞ (|argz | < π)のとき、ポリガンマ関数は次の漸近展開 をもつ。
ψ
(
z
)
∼
ln
z
−
1
2
z
−
∑
n
=
1
∞
B
2
n
2
n
z
2
n
{\displaystyle \psi (z)\sim \ln {z}-{\frac {1}{2z}}-\sum _{n=1}^{\infty }{\frac {B_{2n}}{2nz^{2n}}}}
ψ
(
n
)
(
z
)
∼
(
−
1
)
(
n
−
1
)
(
(
n
−
1
)
!
z
n
+
n
!
2
z
n
+
1
+
∑
k
=
1
∞
B
2
k
(
2
k
+
n
−
1
)
!
(
2
k
)
!
z
2
k
+
n
)
(
n
=
1
,
2
,
⋯
)
{\displaystyle \psi ^{(n)}(z)\sim (-1)^{(n-1)}\left({\frac {(n-1)!}{z^{n}}}+{\frac {n!}{2z^{n+1}}}+\sum _{k=1}^{\infty }{\frac {B_{2k}(2k+n-1)!}{(2k)!z^{2k+n}}}\right)\quad (n=1,2,\cdots )}
但し、B2k はベルヌーイ数 である。
ポリガンマ関数は、m=1において、次の値をとる。
ψ
(
1
)
=
−
γ
{\displaystyle \psi (1)=-\gamma }
ψ
(
n
)
(
1
)
=
(
−
1
)
n
+
1
n
!
ζ
(
n
+
1
)
(
n
=
1
,
2
,
⋯
)
{\displaystyle \psi ^{(n)}(1)=(-1)^{n+1}n!\zeta (n+1)\quad (n=1,2,\cdots )}
ポリガンマ関数は、m≧2の正の整数において、次の値をとる。
ψ
(
m
)
=
−
γ
+
∑
k
=
1
m
−
1
1
k
=
−
γ
+
H
m
−
1
(
m
=
2
,
3
,
4
,
⋯
)
{\displaystyle \psi (m)=-\gamma +\sum _{k=1}^{m-1}{\frac {1}{k}}=-\gamma +H_{m-1}\qquad (m=2,3,4,\cdots )}
ψ
(
n
)
(
m
)
=
(
−
1
)
n
n
!
{
−
ζ
(
n
+
1
)
+
∑
k
=
1
m
−
1
1
k
n
+
1
}
(
n
=
1
,
2
,
3
,
⋯
,
m
=
2
,
3
,
4
,
⋯
)
{\displaystyle \psi ^{(n)}(m)=(-1)^{n}n!\left\{-\zeta (n+1)+\sum _{k=1}^{m-1}{\frac {1}{k^{n+1}}}\right\}\qquad (n=1,2,3,\cdots ,m=2,3,4,\cdots )}
但し、γ はオイラーの定数、Hm-1 は調和数 を表す。