「等角図」の版間の差分
削除された内容 追加された内容
m Template:Weblio廃止のためテンプレート除去、に伴う誤った出典の示し方を修正 / 言語間リンクで節リンクしてるけどこれ正しいのかな？ |
m 過去に教わったのは 等測図（等角図） isometric drawing 等測投影図が isometric projection です。教わった本のコピーでも添付出来れば判り易いとは思いますが どちらだったかwikipediaとかweblio調べていておかしかったので40年ほど前に習った教科書を見ていたら上記の表現でした。 教科書は”実践 テクニカルイラストレーション” 昭和61年初版5刷発行となっています。 |
||
| (10人の利用者による、間の13版が非表示) | |||
| 1行目: | 1行目: | ||
[[ファイル:3D_shapes_in_isometric_projection.svg|サムネイル|等角図で描かれた図形。赤字の寸法は等角図上の長さで、黒字の寸法は[[正投影図]]での実際の長さ。]] |
|||
{{字引|date=2015年10月}} |
|||
| ⚫ | |||
{{出典の明記|date=2015年10月}} |
|||
| ⚫ | |||
[[製図]]の際に用いる図法のひとつで、各辺を実寸で描くことから寸法を伝えやすい利点がある。一方で、奥行きが考慮されないため奥にあるものほど実際よりも大きく描かれる。 |
|||
== 書き方 == |
|||
[[画像:Isometric-1.png|thumb|250px|等角図]] |
|||
水平線と垂直線を書く。水平線に対して、30度の線を書き、幅・奥行き・高さの寸法を実物と同じ割合に取る。それぞれの点から各辺に、平行な線を書き、立体の外形を下書きする。不要な線を消し太い線で仕上げる |
|||
== 歴史 == |
|||
| ⚫ | |||
{{multiple image|width=150|image1=Optical-grinding engine model.jpg|caption1=光学研磨エンジンモデル（1822）の30°等角投影図<ref>William Farish (1822) "On Isometrical Perspective". In: ''Cambridge Philosophical Transactions''. 1 (1822).</ref>|image2=Sanguo2.PNG|caption2=[[中華人民共和国|中国]]の[[明]]代に書かれた[[時代小説]]『[[三国志演義]]』の挿絵}} |
|||
等角図の概念は[[2千年紀]]中期ころ<!--1822年時点から数世紀前とあるため、15-6世紀辺りを想定し「2千年紀中期」と記載-->から[[経験則]]として存在していたが、[[1822年]]に[[化学者]]の{{仮リンク|ウィリアム・ファリッシュ (化学者)|label=ウィリアム・ファリッシュ|en|William Farish (chemist)}}によって初めて定式化された<ref>Barclay G. Jones (1986). ''Protecting historic architecture and museum collections from natural disasters''. University of Michigan. ISBN 0-409-90035-4. p.243.</ref><ref>Charles Edmund Moorhouse (1974). ''Visual messages: graphic communication for senior students''.</ref>。 |
|||
| ⚫ | |||
[[オランダ]]の研究機関{{仮リンク|International Institute for Asian Studies|en|International Institute for Asian Studies}}のJan Krikkeは、「[[等長写像]]は[[19世紀]]半ばから技術者にとって貴重なツールとなり、その後まもなく欧米で[[建築]]訓練のカリキュラムに組み込まれた」「{{仮リンク|軸測投影図|en|Axonometry}}（等角図を含む図法グループの総称）の起源は[[中華人民共和国|中国]]で、中国美術の機能は欧州美術の[[透視投影]]と類似していた」としている<ref>{{cite web|url=https://www.iias.asia/iiasn/iiasn9/eastasia/krikke.html|language=英語|title=IIASN9-Chinese Perspective|publisher=IIAS|accessdate=2019-11-30|archiveurl=https://web.archive.org/web/20190331131123/https://www.iias.asia/iiasn/iiasn9/eastasia/krikke.html|archivedate=2019-3-31}}</ref>。 |
|||
| ⚫ | |||
== 応用 == |
|||
=== トリックアート === |
|||
{{multiple image |
|||
|width=150 |
|||
|image1=IsometricFlaw_2.svg |
|||
|caption1=赤玉よりも青玉のほうが高い位置にあるはずだが、同じ高さのように見える。 |
|||
|image2=Impossible_staircase.svg |
|||
|caption2=[[不可能図形]]として知られる[[ペンローズの階段]]。階段がループした構造で三次元では実現し得ない。 |
|||
}} |
|||
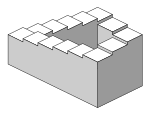
前述のように、等角図は奥行きが正確に表現されない難点がある。しかし、このことを逆に利用し、見る側に[[錯覚]]を与える画像や三次元では構築不可能な[[不可能図形]]といった[[トロンプ・ルイユ|トリックアート]]の数々が制作されている。 |
|||
{{Clear}} |
|||
=== コンピュータゲーム === |
|||
{{main|:en:Isometric video game graphics}} |
|||
1980年代から1990年代のコンピュータゲームの一部では、等角図のような斜め見下ろし視点の「[[クォータービュー]]」表現が見られた。これは、当時の技術では3D表現が困難だったことから、限られたリソースの中で擬似的に3Dに見せる手法として用いられたものである。 |
|||
クォータービューを初めて採用したゲームは1982年に[[セガ]]が発売した[[アーケードゲーム|アーケード]]向け[[シューティングゲーム]]『[[ザクソン]]』で、1990年代には『[[ディアブロ (ゲーム)|ディアブロ]]』『[[バルダーズ・ゲート]]』『[[スタークラフト]]』『{{仮リンク|X-COM: UFO Defense|en|X-COM: UFO Defense}}』などの[[パーソナルコンピュータ|PC]]向けの[[コンピュータRPG|RPG]]や[[ストラテジーゲーム]]で多く採用された。2000年代に入りグラフィックの表現力が増すにつれてクォータービュー作品は減少したが、2010年代頃からは一部の[[インディーゲーム]]で採用されている<ref>{{Cite web|url=https://www.usgamer.net/articles/twisted-perspective-the-continued-relevance-of-isometric-games|language=英語|title=Retronauts: The Continued Relevance of Isometric Games|publisher=USgamer|date=2014-12-19|accessdate=2022-12-12}}</ref>。 |
|||
{{Clear}} |
|||
| ⚫ | |||
{{脚注ヘルプ}} |
{{脚注ヘルプ}} |
||
{{Reflist}} |
{{Reflist}} |
||
| ⚫ | |||
{{ウィキプロジェクトリンク|数学|[[画像:Nuvola apps edu mathematics blue-p.svg|34px|Project:数学]]}} |
|||
| ⚫ | |||
{{ウィキポータルリンク|数学|[[画像:Nuvola apps edu mathematics-p.svg|34px|Portal:数学]]}} |
|||
* {{cite encyclopedia |editor=日本大辞典刊行会 |year=1974 |title |
* {{cite encyclopedia |editor=日本大辞典刊行会 |year=1974 |title=とうかくとうえいず【等角投影図】 |page=425 |encyclopedia=大日本国語辞典 |volume=14 |edition=初版初刷 |publisher=小学館 |location=東京 |id={{NCID|BN01221521}} |isbn=4095220147}} |
||
== 外部リンク == |
== 外部リンク == |
||
{{ |
{{Commonscat|Isometric projection}} |
||
*{{Kotobank|等角投影図}} |
* {{Kotobank|等角投影図}} |
||
| ⚫ | |||
| ⚫ | |||
{{DEFAULTSORT:とうかくす}} |
{{DEFAULTSORT:とうかくす}} |
||
[[Category:ダイアグラム]] |
[[Category:ダイアグラム]] |
||
[[Category:幾何学]] |
[[Category:幾何学]] |
||
[[Category:数学に関する記事]] |
[[Category:数学に関する記事]] |
||
[[de:Perspektive#Isometrische Axonometrie, nach DIN 5]] |
|||
[[it:Assonometria#Assonometria isometrica]] |
|||
2024年5月24日 (金) 00:17時点における最新版
等角図（とうかくず、英: isometric drawing）または等角投影図（とうかくとうえいず、英:isometric projection）は、投影図のひとつ。直交する3軸の角度をそれぞれ120度とし[1]、物体を斜め上から俯瞰したように描写される。
製図の際に用いる図法のひとつで、各辺を実寸で描くことから寸法を伝えやすい利点がある。一方で、奥行きが考慮されないため奥にあるものほど実際よりも大きく描かれる。
歴史
[編集]
等角図の概念は2千年紀中期ころから経験則として存在していたが、1822年に化学者のウィリアム・ファリッシュによって初めて定式化された[3][4]。
オランダの研究機関International Institute for Asian StudiesのJan Krikkeは、「等長写像は19世紀半ばから技術者にとって貴重なツールとなり、その後まもなく欧米で建築訓練のカリキュラムに組み込まれた」「軸測投影図（等角図を含む図法グループの総称）の起源は中国で、中国美術の機能は欧州美術の透視投影と類似していた」としている[5]。
応用
[編集]トリックアート
[編集]
前述のように、等角図は奥行きが正確に表現されない難点がある。しかし、このことを逆に利用し、見る側に錯覚を与える画像や三次元では構築不可能な不可能図形といったトリックアートの数々が制作されている。
コンピュータゲーム
[編集]→詳細は「en:Isometric video game graphics」を参照
1980年代から1990年代のコンピュータゲームの一部では、等角図のような斜め見下ろし視点の「クォータービュー」表現が見られた。これは、当時の技術では3D表現が困難だったことから、限られたリソースの中で擬似的に3Dに見せる手法として用いられたものである。
クォータービューを初めて採用したゲームは1982年にセガが発売したアーケード向けシューティングゲーム『ザクソン』で、1990年代には『ディアブロ』『バルダーズ・ゲート』『スタークラフト』『X-COM: UFO Defense』などのPC向けのRPGやストラテジーゲームで多く採用された。2000年代に入りグラフィックの表現力が増すにつれてクォータービュー作品は減少したが、2010年代頃からは一部のインディーゲームで採用されている[6]。
脚注
[編集]- ^ 日本大辞典刊行会 1974.
- ^ William Farish (1822) "On Isometrical Perspective". In: Cambridge Philosophical Transactions. 1 (1822).
- ^ Barclay G. Jones (1986). Protecting historic architecture and museum collections from natural disasters. University of Michigan. ISBN 0-409-90035-4. p.243.
- ^ Charles Edmund Moorhouse (1974). Visual messages: graphic communication for senior students.
- ^ “IIASN9-Chinese Perspective” (英語). IIAS. 2019年3月31日時点のオリジナルよりアーカイブ。2019年11月30日閲覧。
- ^ “Retronauts: The Continued Relevance of Isometric Games” (英語). USgamer (2014年12月19日). 2022年12月12日閲覧。
参考文献
[編集]
- 日本大辞典刊行会, ed. (1974). "とうかくとうえいず【等角投影図】". 大日本国語辞典. Vol. 14 (初版初刷 ed.). 東京: 小学館. p. 425. ISBN 4095220147. NCID BN01221521。
外部リンク
[編集]
 | この項目は、幾何学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（プロジェクト:数学／Portal:数学）。 |