「零写像」の版間の差分

削除された内容追加された内容

インライン

2021年4月16日 (金) 09:37時点における最新版

数学における零写像（れいしゃぞう、ゼロしゃぞう、英: zero mapping）は、零元を持つ適当な代数系^{[注釈 1]}への写像であって、その定義域の全ての元を終域の零元へ写すものを言う。殊に、解析学における零函数 (zero function) は、変数の値によらず函数値が常に零となるような函数を言う。また、線型代数学におけるベクトル空間の間の零（線型）写像 (zero map) または零（線型）作用素 (zero operator) は、全てのベクトルを零ベクトルに写す。

零写像は多くの性質を満足し、数学において例や反例としてしばしば用いられる。零写像は斉次線型微分方程式や積分方程式などの数学の一連の問題において、自明な解（ドイツ語版）になる。

実零函数[編集]

定義[編集]

実解析における実零函数は、実函数 $φ : R \to R$ であって、すべての引数に $0$ を割り当てるもの、すなわち

\varphi (x)=0\quad (\forall x\in \mathbb {R} )

を満足するものを言う。恒等式の記法を用いれば、零函数であることを「

φ \equiv 0

」とも書ける。

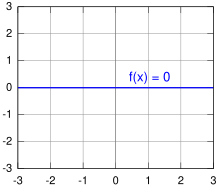
零函数のグラフは $x$ -軸全体に一致する。場合によっては零函数の定義域を部分集合 $Ω \subset R$ に制限することもある。

性質[編集]

分類[編集]

零函数は以下のような函数のクラスの特別の場合になっている:

定数函数 $f (x) = c$ の、定数 $c = 0$ となる特別の場合。
一次函数 $f (x) = mx + b$ の、傾き $m = 0$ かつ截片 $b = 0$ となる特別の場合。
多項式函数 $f (x) = a n x n + \dots + a 1 x + a 0$ の全ての係数が $a i = 0$ （すなわち零多項式）である場合。零多項式の次数はふつう、 $0$ ではなく $-\infty$ と定義される。

対称性[編集]

零函数は偶かつ奇函数、すなわち ${\textstyle \phi (x)=\phi (-x)=-\phi (x)}$ が成り立つ。
零函数は正値函数でも負値函数でもない^{[注釈 2]}。が、非正値かつ非負値（すなわち ${\textstyle \phi (x)\leq 0\wedge \phi (x)\geq 0}$ ）である。
零函数の零点全体の成す集合は定義域全体に一致し、非零点集合（ドイツ語版）（集合論の意味での台）は空集合である。零函数の最大値および最小値はともに零: $\max _{x\in \mathbb {R} }\phi (x)=\min _{x\in \mathbb {R} }\phi (x)=0$ である。
零函数は、すべての定数函数がそうであるように、広義単調増大かつ広義単調減少（狭義ではダメ）である。
零函数は、すべての一次函数がそうであるように、凸かつ凹である。

微分[編集]

零函数は滑らかな函数、すなわち何回でも連続的微分可能であり、その各階の導函数は零函数で与えられる。すなわち

\varphi ^{(n)}(x)=\varphi (x)\equiv 0\quad (\forall n\in \mathbb {N} )

が成り立つ。指数函数を除けば、このような性質を持つ函数は零函数に限る。

零函数自体は、定数函数の導函数として、あるいは一般に $n$ -次多項式函数の $(n + 1)$ -階導函数として得ることができる。

積分[編集]

零函数の定積分は、積分の限界の取り方に依らず常に零である。すなわち

\int _{a}^{b}\phi (x)\,dx=0\quad (\forall a,b\in {\bar {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,\infty \})

が成り立つ。

したがって、零函数は実数直線全体で可積分な唯一の多項式函数である。零函数の原始函数は、不定積分の積分定数は任意にとれるから、零函数自身も含めた任意の定数函数によって与えられる。

方程式の解[編集]

零函数はコーシーの四つの函数方程式:

{\begin{aligned}f(x+y)&=f(x)+f(y)\\f(x+y)&=f(x)\cdot f(y)\\f(x\cdot y)&=f(x)+f(y)\\f(x\cdot y)&=f(x)\cdot f(y)\end{aligned}}

の自明な解である。^[2]

さらに、零函数は

a_{n}(x)f^{(n)}(x)+a_{n-1}(x)f^{(n-1)}+\dotsb +a_{1}(x)f'(x)+a_{0}(x)f(x)=0

なる形の斉次線型微分方程式の自明な解であり、また

\lambda f(x)+\int _{a}^{x}K(x,y)f(y)\,dy=0

（

K (x, y)

は積分核、

λ

は前因子）なる形の積分方程式の自明な解である。逆に非斉次の線型微分または積分方程式が零函数を解に持つことはない。

零線型写像[編集]

定義[編集]

線型代数学において、同じ体 $K$ 上の二つのベクトル空間 $V, W$ の間の写像 $φ : V \to W$ が零写像または零作用素であるとは、 $V$ の全てのベクトルを $W$ の唯一の零ベクトル $0 W$ へ写す写像

\phi (v)=0_{W}\quad (\forall v\in V)

を言う。

零写像も $0$ で表すことがある（文脈から数値の $0$ か零写像の $0$ かが文脈から明らかである場合に限る）。零写像も定義域を部分集合 $U \subset V$ に制限することができる。

例[編集]

上で述べた実零函数、あるいはより一般に実または複素一変数または多変数の函数で、その値が常に零または零ベクトルであるようなものはすべて本節の意味での零写像の例である。
任意のベクトル空間 $V$ から零ベクトル空間 ${0}$ への任意の写像、および零ベクトル空間から任意のベクトル空間 $W$ への線型写像は必ず零写像である^[3]。
任意の正方行列をその固有多項式に代入してえられる行列が定める線型写像が零写像となることはケイリー-ハミルトンの定理による^[4]。
非正則な正方行列全体の成す部分集合上で、行列式函数（ドイツ語版）は零写像である^[5]。

性質[編集]

線型性[編集]

零写像は線型写像である。すなわち、ベクトル空間の間の準同型として

\phi (av+bw)=a\phi (v)+b\phi (w)\quad (\forall v,w\in V,\,a,b\in K)

を満足する。したがって零写像は、線型写像全体の成すベクトル空間

L (V, W)

に属し、そのベクトル空間の零ベクトルとなる。

有限次元ベクトル空間の間の零写像は、それぞれの空間の基底をどのように選んでも、サイズ $dim V \times dim W$ の零行列で表現される^[6]。零写像の核は $V$ 全体で、像は ${0 W}$ であり、したがって階数は常に $0$ である。 $V = W$ のとき、固有値はすべて $0$ であり、固有空間は $V$ となる。

作用素ノルム[編集]

$V, W$ がノルム空間で、それぞれのノルムを $‖ • ‖ V, ‖ • ‖ W$ とすれば、零写像の作用素ノルムは

\|\phi \|=\sup _{\|v\|_{V}=1}\|\phi (v)\|_{W}=\|0_{W}\|_{W}=0

となる。

W = R

に対して零写像自身が半ノルムを成す。

方程式の解[編集]

一般に零写像は、未知函数 $u$ に関する任意の斉次線型作用素方程式

{\mathcal {L}}u=0\quad ({\mathcal {L}}\in L(V,W))

を満足する。ただし、右辺の

0

は零写像の意味である。逆に、右辺を零写像以外に取り換えて得られる任意の非斉次線型作用素方程式において零写像は解にならない。

零準同型[編集]

定義[編集]

$X$ を集合、 $Y$ を単位的マグマ（つまり、結合 $*$ とそれに関する単位元 $0$ を持つ集合）とすれば、写像 $φ : X \to Y$ が零写像であるとは、

\varphi (x)=0\quad (\forall x\in X)

を満たすときに言う。そのような代数系

(Y, *)

としてモノイド、群、環、加群やうえで述べたベクトル空間などが重要な例として挙げることができる。

例[編集]

ブール環またはブール代数に値をとる、矛盾に対応するブール函数。
$q$ -元体上の多項式環における多項式函数 $x \mapsto x q - x$ . ^[7]
環に値をとる冪零写像の $k$ -回合成冪、ただし $k$ が像の冪零度以上であるとき。^[8]
任意の集合 $A$ が零集合 $μ (A) = 0$ となるような測度 $μ$ .

性質[編集]

$X$ がマグマで $Y$ が単位的マグマのとき、零写像はマグマ準同型である。
$X, Y$ が二つの単位的環のとき、零写像は環準同型である。 $X$ が単純環（例えば可換体または斜体）ならば、任意の環準同型は単射であるかさもなくば零写像である^[9]。
$X, Y$ が二つの加群のとき、零写像は加群準同型である。
$X, Y$ が二つの多元環のとき、零写像は多元環準同型（英語版）である。

注[編集]

注釈[編集]

^ もっとも一般の場合（演算の型が空の場合）として、点付き集合が考えられる。そのとき零元としては基点を考えればよい。^[1]
^ ここに「正値函数」は、単にそれぞれ真に正の値を常にとる函数 (strictly positive-valued function) の意味で用いる（負値も同様）。「正定値函数」や「正の定符号函数」ともいうが、二次形式や行列論に関連してやや異なる意味（英語版）で用いられることも多いので注意すべきである。

出典[編集]

^ zero function in nLab
^ Barner, Flohr, Analysis I (ドイツ語), p. 247
^ Bosch, Lineare Algebra (ドイツ語), p. 78
^ Bosch, Lineare Algebra (ドイツ語), p. 204
^ Bosch, Lineare Algebra (ドイツ語), p. 141
^ Bosch, Lineare Algebra (ドイツ語), p. 93
^ Karpfinger, Meyberg, Algebra: Gruppen – Ringe – Körper (ドイツ語), p. 158
^ Karpfinger, Meyberg, Algebra: Gruppen – Ringe – Körper (ドイツ語), p. 181
^ Karpfinger, Meyberg, Algebra: Gruppen – Ringe – Körper (ドイツ語), p. 172

参考文献[編集]

Martin Barner, Friedrich Flohr (2000), Analysis I (ドイツ語), de Gruyter, ISBN 3-110-16778-6。
Siegfried Bosch (2009), Lineare Algebra (ドイツ語), Springer, ISBN 3-540-76437-2。
Christian Karpfinger, Kurt Meyberg (2008), Algebra: Gruppen – Ringe – Körper (ドイツ語), Springer, ISBN 3-827-42018-0。
Gilbert Strang (2003), Lineare Algebra (ドイツ語), Springer, ISBN 3-540-43949-8。

外部リンク[編集]

Barile, Margherita. "Zero Map". mathworld.wolfram.com (英語).
zero function in nLab
Zero Map - PlanetMath.（英語）
Definition:Zero Homomorphism at ProofWiki

[2] もっとも一般の場合（演算の型が空の場合）として、点付き集合が考えられる。そのとき零元としては基点を考えればよい。^[1]

[3] ここに「正値函数」は、単にそれぞれ真に正の値を常にとる函数 (strictly positive-valued function) の意味で用いる（負値も同様）。「正定値函数」や「正の定符号函数」ともいうが、二次形式や行列論に関連してやや異なる意味（英語版）で用いられることも多いので注意すべきである。

[1] zero function in nLab

[4] Barner, Flohr, Analysis I (ドイツ語), p. 247

[5] Bosch, Lineare Algebra (ドイツ語), p. 78

[6] Bosch, Lineare Algebra (ドイツ語), p. 204

[7] Bosch, Lineare Algebra (ドイツ語), p. 141

[8] Bosch, Lineare Algebra (ドイツ語), p. 93

[9] Karpfinger, Meyberg, Algebra: Gruppen – Ringe – Körper (ドイツ語), p. 158

[10] Karpfinger, Meyberg, Algebra: Gruppen – Ringe – Körper (ドイツ語), p. 181

[11] Karpfinger, Meyberg, Algebra: Gruppen – Ringe – Körper (ドイツ語), p. 172

[注釈 1]

[注釈 2]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[1]

@@ 41行目: / 41行目: @@
 f(x \cdot y) & = f(x) \cdot f(y)
 \end{align}</math>
-の自明な解である。<ref>{{Literatur|Autor=Barner, Flohr|Titel=Analysis I|Seiten=247}}</ref>
+の自明な解である。<ref>{{citation2|surname1=Barner, Flohr|title=Analysis I|at=p.&nbsp;247|language=de
+}}</ref>
 さらに、零函数は <math display="block">a_n(x) f^{(n)}(x) + a_{n-1}(x) f^{(n-1)} + \dotsb + a_1(x) f'(x) + a_0(x) f(x) = 0</math> なる形の斉次[[線型微分方程式]]の自明な解であり、また <math display="block">\lambda f(x) + \int_a^x K(x,y) f(y)\,dy = 0</math>（{{math|''K''(''x'', ''y'')}} は[[積分核]]、{{mvar|λ}} は前因子）なる形の[[積分方程式]]の自明な解である。逆に非斉次の線型微分または積分方程式が零函数を解に持つことはない。
@@ 53行目: / 54行目: @@
 === 例 ===
 * 上で述べた実零函数、あるいはより一般に[[実数|実]]または[[複素数|複素]]一変数または多変数の函数で、その値が常に零または零ベクトルであるようなものはすべて本節の意味での零写像の例である。
-* 任意のベクトル空間 {{mvar|V}} から[[零ベクトル空間]] {{math|{{mset|0}}}} への任意の写像、および零ベクトル空間から任意のベクトル空間 {{mvar|W}} への[[線型写像]]は必ず零写像である<ref>{{Literatur|Autor=Bosch|Titel=Lineare Algebra|Seiten=78}}</ref>。
+* 任意のベクトル空間 {{mvar|V}} から[[零ベクトル空間]] {{math|{{mset|0}}}} への任意の写像、および零ベクトル空間から任意のベクトル空間 {{mvar|W}} への[[線型写像]]は必ず零写像である<ref>{{citation2|surname1=Bosch|title=Lineare Algebra|at=p.&nbsp;78|language=de
+}}</ref>。
-* 任意の[[正方行列]]をその[[固有多項式]]に[[汎函数計算|代入]]してえられる行列が定める線型写像が零写像となることは[[ケイリー-ハミルトンの定理]]による<ref>{{Literatur|Autor=Bosch|Titel=Lineare Algebra|Seiten=204}}</ref>。
+* 任意の[[正方行列]]をその[[固有多項式]]に[[汎函数計算|代入]]してえられる行列が定める線型写像が零写像となることは[[ケイリー-ハミルトンの定理]]による<ref>{{citation2|surname1=Bosch|title=Lineare Algebra|at=p.&nbsp;204|language=de
+}}</ref>。
-* [[正則行列|非正則]]な正方行列全体の成す部分集合上で、{{ill2|行列式函数|de|Determinantenfunktion}}は零写像である<ref>{{Literatur|Autor=Bosch|Titel=Lineare Algebra|Seiten=141}}</ref>。
+* [[正則行列|非正則]]な正方行列全体の成す部分集合上で、{{ill2|行列式函数|de|Determinantenfunktion}}は零写像である<ref>{{citation2|surname1=Bosch|title=Lineare Algebra|at=p.&nbsp;141|language=de
+}}</ref>。
 === 性質 ===
@@ 61行目: / 65行目: @@
 零写像は[[線型写像]]である。すなわち、ベクトル空間の間の準同型として <math display="block">\phi(av + bw) = a\phi(v) + b\phi(w)\quad (\forall v,w\in V,\,a,b\in K)</math> を満足する。したがって零写像は、線型写像全体の成すベクトル空間 {{math|''L''(''V'', ''W'')}} に属し、そのベクトル空間の零ベクトルとなる。
-有限次元ベクトル空間の間の零写像は、それぞれの空間の基底をどのように選んでも、サイズ {{math|dim ''V'' × dim ''W''}} の[[零行列]]で表現される<ref>{{Literatur|Autor=Bosch|Titel=Lineare Algebra|Seiten=93}}</ref>。零写像の[[核 (代数学)|核]]は {{mvar|V}} 全体で、[[像 (数学)|像]] は {{math|{{mset|0{{sub|''W''}}}}}} であり、したがって[[行列の階数|階数]]は常に {{math|0}} である。{{math|1=''V'' = ''W''}} のとき、[[固有値]]はすべて {{math|0}} であり、固有空間は {{mvar|V}} となる。
+有限次元ベクトル空間の間の零写像は、それぞれの空間の基底をどのように選んでも、サイズ {{math|dim ''V'' × dim ''W''}} の[[零行列]]で表現される<ref>{{citation2|surname1=Bosch|title=Lineare Algebra|at=p.&nbsp;93|language=de
+}}</ref>。零写像の[[核 (代数学)|核]]は {{mvar|V}} 全体で、[[像 (数学)|像]] は {{math|{{mset|0{{sub|''W''}}}}}} であり、したがって[[行列の階数|階数]]は常に {{math|0}} である。{{math|1=''V'' = ''W''}} のとき、[[固有値]]はすべて {{math|0}} であり、固有空間は {{mvar|V}} となる。
 ==== 作用素ノルム ====
@@ 75行目: / 80行目: @@
 === 例 ===
 * [[ブール環]]または[[ブール代数]]に値をとる、[[矛盾]]に対応する[[ブール函数]]。
-* [[有限体|{{mvar|q}}-元体]]上の[[多項式環]]における[[多項式函数]] {{math|''x'' {{mapsto}} ''x{{exp|q}}'' &minus; ''x''}}. <ref>{{Literatur|Autor=Karpfinger, Meyberg|Titel=Algebra: Gruppen – Ringe – Körper|Seiten=158}}</ref>
+* [[有限体|{{mvar|q}}-元体]]上の[[多項式環]]における[[多項式函数]] {{math|''x'' {{mapsto}} ''x{{exp|q}}'' &minus; ''x''}}. <ref>{{citation2|surname1=Karpfinger, Meyberg|title=Algebra: Gruppen – Ringe – Körper|at=p.&nbsp;158|language=de
+}}</ref>
-* 環に値をとる[[冪零]]写像の [[反復合成写像|{{mvar|k}}-回合成冪]]、ただし {{mvar|k}} が像の冪零度以上であるとき。<ref>{{Literatur|Autor=Karpfinger, Meyberg|Titel=Algebra: Gruppen – Ringe – Körper|Seiten=181}}</ref>
+* 環に値をとる[[冪零]]写像の [[反復合成写像|{{mvar|k}}-回合成冪]]、ただし {{mvar|k}} が像の冪零度以上であるとき。<ref>{{citation2|surname1=Karpfinger, Meyberg|title=Algebra: Gruppen – Ringe – Körper|at=p.&nbsp;181|language=de
+}}</ref>
 * 任意の集合 {{mvar|A}} が[[零集合]] {{math|1=''μ''(''A'') = 0}} となるような[[測度]] {{mvar|μ}}.
 === 性質 ===
 * {{mvar|X}} がマグマで {{mvar|Y}} が単位的マグマのとき、零写像は[[マグマ準同型]]である。
-* {{mvar|X, Y}} が二つの[[単位的環]]のとき、零写像は[[環準同型]]である。{{mvar|X}} が[[単純環]]（例えば[[可換体]]または[[斜体 (数学)|斜体]]）ならば、任意の環準同型は[[単射]]であるかさもなくば零写像である<ref>{{Literatur|Autor=Karpfinger, Meyberg|Titel=Algebra: Gruppen – Ringe – Körper|Seiten=172}}</ref>。
+* {{mvar|X, Y}} が二つの[[単位的環]]のとき、零写像は[[環準同型]]である。{{mvar|X}} が[[単純環]]（例えば[[可換体]]または[[斜体 (数学)|斜体]]）ならば、任意の環準同型は[[単射]]であるかさもなくば零写像である<ref>{{citation2|surname1=Karpfinger, Meyberg|title=Algebra: Gruppen – Ringe – Körper|at=p.&nbsp;172|language=de
+}}</ref>。
 * {{mvar|X, Y}} が二つの[[環上の加群|加群]]のとき、零写像は[[加群準同型]]である。
 * {{mvar|X, Y}} が二つの[[環上の多元環|多元環]]のとき、零写像は{{ill2|多元環準同型|en|Algebra homomorphism}}である。
@@ 98行目: / 106行目: @@
 == 参考文献 ==
-* {{Literatur|Autor=Martin Barner, Friedrich Flohr|Titel=Analysis I|Verlag=de Gruyter|Jahr=2000|ISBN=3-110-16778-6}}
+* {{citation2|surname1=Martin Barner, Friedrich Flohr|title=Analysis I|publisher=de Gruyter|year=2000|isbn=3-110-16778-6|language=de
+}}
-* {{Literatur|Autor=[[Siegfried Bosch]]|Titel=Lineare Algebra|Verlag=Springer|Jahr=2009|ISBN=3-540-76437-2}}
+* {{citation2|surname1=[[Siegfried Bosch]]|title=Lineare Algebra|publisher=Springer|year=2009|isbn=3-540-76437-2|language=de
+}}
-* {{Literatur|Autor=Christian Karpfinger, Kurt Meyberg|Titel=Algebra: Gruppen – Ringe – Körper|Verlag=Springer|Jahr=2008|ISBN=3-827-42018-0}}
+* {{citation2|surname1=Christian Karpfinger, Kurt Meyberg|title=Algebra: Gruppen – Ringe – Körper|publisher=Springer|year=2008|isbn=3-827-42018-0|language=de
-* {{Literatur|Autor=[[Gilbert Strang]]|Titel=Lineare Algebra|Verlag=Springer|Jahr=2003|ISBN=3-540-43949-8}}
+}}
+* {{citation2|surname1=[[Gilbert Strang]]|title=Lineare Algebra|publisher=Springer|year=2003|isbn=3-540-43949-8|language=de
+}}
 == 外部リンク ==

2021年4月16日 (金) 09:37時点における最新版

実零函数[編集]

定義[編集]

性質[編集]

分類[編集]

対称性[編集]

微分[編集]

積分[編集]

方程式の解[編集]

零線型写像[編集]

定義[編集]

例[編集]

性質[編集]

線型性[編集]

作用素ノルム[編集]

方程式の解[編集]

零準同型[編集]

定義[編集]

例[編集]

性質[編集]

関連項目[編集]

注[編集]

注釈[編集]

出典[編集]

参考文献[編集]

外部リンク[編集]