ハニカム構造


ハニカム構造(ハニカムこうぞう、英語:honeycomb structure)とは、正六角形または正六角柱を隙間なく並べた構造である。ハニカムとは英語で「ミツバチの巣」という意味であり、多くの蜂の巣がこのような形をしていることから名付けられた。
広義には、正六角柱に限らず立体図形を隙間なく並べたもの(3次元空間充填)をハニカムと呼ぶ。
板状の素材に孔を開ければ、強度をあまり損なわずに必要な材料を減らすことができる。孔の大きさや数をどんどん増やせば、最終的には棒材による構造が残る。同様に、塊状の素材に孔を開ければ、板材による構造が残る。これらがハニカムである。
ハニカムの形
[編集]
孔を小さくすれば強度は増すが、単位面積あたり棒材の量は増える。そこで、孔の面積を一定にして、最も棒材の量が少なくなる孔の開け方を考える。これは、
同じ面積の図形による平面充填で、周の長さが最も短いのは何か
という数学的問題にできる。またこうすることで、強度と材料の量の関係に限らないさまざまな課題に一般化できる。
同じ面積で最も周が短い図形は円である。しかし円で平面を充填しようとすると歪な形の隙間が残り、円だけで充填することはできない。平面充填可能な図形には、三角形、四角形、平行六角形などがあるが、最も周が短いのは正六角形である。これは、平面充填形の中で正六角形が最も円に近いことからも直感的に理解できる。
同様に、3次元での
同じ体積の図形による3次元空間充填で、表面積が最も狭いのは何か
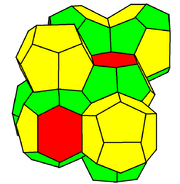
という問題(「ケルヴィン問題」)を考えることができる。この問題は未解決だが、既知の最適な答えはウィア=フェラン構造と呼ばれる等体積の12面体と14面体からなる充填である(1993年にこれが発見されるまでは切頂八面体がそうだった)。しかし、ある種の制約(例えば、孔が貫通していなければならない、問題となる空間が薄っぺらい、複雑な立体加工はできない、など)の下では、正六角柱が答えとなる。
自然界のハニカム構造
[編集]-
玄武岩の柱状節理
-
トンボの複眼
-
亀の甲羅
応用
[編集]


輸送機器
[編集]- 航空機においては、サンドイッチ構造のコア材料の一種として、アルミニウム合金やノーメックス製のハニカムが使用されている。モスキート爆撃機は戦時の金属原料不足に対して、木製ボディで挟んだペーパーハニカム構造を採用して、コストダウンと軽量化に成功した。
- 新幹線において、500系新幹線の車体には、世界初となる曲面のアルミろう付ハニカムパネルが採用され、N700系新幹線のガイシオオイ(パンタグラフカバー)にろう付ハニカムパネルが採用された。
- 戦車等の複合装甲のセラミックス製構造材に使用される場合がある。例)英陸軍チャレンジャー主力戦闘戦車の「チョバム・アーマー」
- F1を始めとするレーシングカーのモノコックや外板 等においても、サンドイッチ構造のコア材料の一種として、アルミやアラミド繊維のハニカムが使用されている。以前は表板/中芯ともアルミが主流であった。1990年代前後より表板は炭素繊維強化プラスチックに取って代わられつつあるが、エントリーカテゴリのモノコック等には依然アルミが使用されている。
- 自動車の排気ガスを清浄化する触媒担体。
建築材料
[編集]- ハニカムビームは鉄骨のH型鋼材のウェブ部分を台形に切り込んで上下に溶接することにより加工される梁材(組み合わされた時に六角形のスリーブができ、設備配管を通すことができる)。
音響機器
[編集]その他
[編集]- サッカーゴールの網は従来、格子状の網を用いていたが、2000年前後よりシュートしたボールがネットに絡めとられ、ゴールに突き刺さるように見えると言う演出的な理由によりハニカム状のネットが採用されるようになった。
- 薄さと軽さと強度が求められる一眼レフカメラ(特に高速なシャッター速度を実現している機種)のシャッター幕では、表面にハニカム構造の採用がみられる。
- デジタルカメラでは、富士フイルムが「スーパーCCDハニカム」というCCDイメージセンサ技術を採用している。これは八角形のCCD素子を利用したシステムである。
- 眼鏡のレンズでは、株式会社 レブラ(旧サクサン オプティカル)[1]社から「ネッツペックコーテング(NPコート)」が施された、高機能レンズRevra:レブラがある。これは、ハニカム構造をした金属膜をレンズ表面に貼り、 透過率の異なった光の減光域を作る事で光を干渉させ、透過率は従来のクリアレンズと同等でありながら、防眩効果や高コントラスト性を高めたものである。
- 原子レベルにおいてのハニカム構造も考えられており、六角形に結合された炭素が他の六角形と結合され円筒型の構造を作り出すことによってあらゆる原子結合で最も強い結合が生み出される。この新素材は「カーボンナノチューブ」と呼ばれ、アルミニウムの約半分の軽さ、鋼鉄の100倍の強度、ダイヤモンドの2倍の硬さを持つ。この素材は将来、宇宙へ行くためのエレベーターを作り出す上で必要になる素材の一つではないかとされている。



