ひずみ (化学)
化学において、分子は、その化学構造がひずみの無い基準化合物と比較してその内部エネルギーを上昇するようなある種の応力を受けた時にひずみ(英: Strain)を受ける。分子の内部エネルギーはその内部に蓄えられる全てのエネルギーから成る。ひずんだ分子は、ひずんでいない分子が持っていない追加の内部エネルギーを持っている。この追加の内部エネルギー(ひずみエネルギー)は圧縮されたばねに例えることができる[1]。圧縮されたばねがそのポテンシャルエネルギーの放出するのを妨げるために適切な位置で保持しなければならないのと同じように、分子は分子内の結合によってエネルギー的に好ましくない配座に保持されうる。配座を適切な位置で支える結合がなければ、ひずみエネルギーは解放される。
概要
[編集]熱力学
[編集]2つの分子配座の平衡は2つの配座のギブズの自由エネルギーにおける差によって決定される。このエネルギー差から、2つの配座に対する平衡定数を決定できる。
ある状態から別の状態へギブズの自由エネルギーが減少するならば、この変換は自発的であり、より低いエネルギー状態がより安定である。高度にひずんだ、より高いエネルギーを持つ分子配座は自発的により低いエネルギーの分子配座へと変換する。

エンタルピーおよびエントロピーは(一定温度において)以下の式によってギブズの自由エネルギーと関連している。
エンタルピーが通常は、より安定な分子配座を決定するためにより重要な熱力学的関数である[1]。ひずみには複数の異なる種類が存在するものの、それら全てに関連するひずみエネルギーは分子内の結合が弱くなることが原因である。エンタルピーが通常はより重要であるため、エントロピーはしばしば無視することができる[1]。これが常に当てはまる訳ではない。エンタルピーの差が小さければ、エントロピーが平衡に関してより大きな影響を持ちうる。例えば、n-ブタンはアンチとゴーシュの2つの可能な配座を持つ。アンチ配座の方が0.9 kcal/mol安定である[1]。室温では、ブタンはおおよそ82%がアンチ形、18%がゴーシュ形であると予測できる。しかしながら、ゴーシュ形には2種類あるのに対してアンチ形は1種類しか存在しない。したがって、エントロピーは、ゴーシュ配座が有利となる方に0.4 kcal/molの寄与をする[2]。その結果、室温におけるブタンの実際の配座分布は70%がアンチ形、30%がゴーシュ形である。
分子のひずみの決定
[編集]
化合物の生成熱(ΔHfo)は、それぞれ分かれた元素からその化合物が形成された時のエンタルピー変化として記述される[3]。化合物に対する生成熱が予測または基準化合物と異なる時、この差はしばしばひずみが原因である。例えば、シクロヘキサンのΔHfoが−29.9 kcal/molであるのに対して、メチルシクロペンタンのΔHfoは−25.5 kcal/molである[1]。同じ原子と結合の数を持つにもかかわらず、メチルシクロペンタンはシクロヘキサンよりもエネルギー的に高い。このエネルギー差は、シクロヘキサンでは見られない5員環の環ひずみに起因する。実験的には、ひずみエネルギーは、簡単に実験することができる燃焼熱を用いてしばしば決定される。
分子内のひずみエネルギーの決定は、ひずみなしでの予測される内部エネルギーの知識を必要とする。これを行うためには2つのやり方がある。一つ目は、前述したシクロヘキサンとメチルシクロペンタンの例のように、ひずみを持たない類似化合物と比較する方法である。不運なことに、適した化合物を得るのは困難なことが多い。別の方法は、ベンソンの加性則を用いる。化合物内の原子について適切なグループ・インクリメントが利用可能な限り、ΔHfoの推算が可能である。実験的なΔHfoと予測されたΔHfoが異なるとすると、このエネルギー差はひずみエネルギーに帰することができる。
ひずみの種類
[編集]ファンデルワールスひずみ
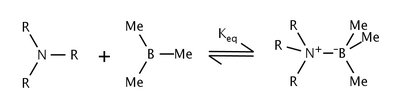
[編集]ファンデルワールスひずみ(立体ひずみ)は、原子がそれらのファンデルワールス半径が許容するよりも接近せざるをえない時に起こる。具体的には、ファンデルワールスひずみは、相互作用している原子同士が互いに少なくとも4結合離れている時のひずみの形式であると考えられる[4]。類似分子における立体ひずみの量は相互作用する基の大きさに依存する。嵩高いtert-ブチル基はメチル基よりも大きな空間を占め、しばしばより大きな立体相互作用を受ける。
トリアルキルアミンとトリメチルボランとの反応における立体ひずみの効果はブラウンらによって研究された[5]。ブラウンらは、アミン上のアルキル基の大きさが増大するにつれて、平衡定数も同様に低下することを見出した。平衡の変化は、アミンのアルキル基とホウ素上のメチル基との間の立体ひずみが原因であるとされた。
syn-ペンタンひずみ
[編集]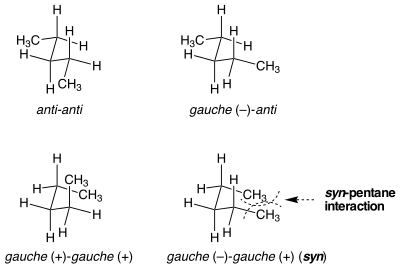
一見同一の配座のひずみエネルギーが等しくない状況が存在する。syn-ペンタンひずみがこの状況の一例である。n-ペンタンの真ん中の2つの結合をゴーシュ配座にするやり方には2種類があり、一方はもう一方よりもエネルギー的に3 kcal/mol高い[1]。2つのメチル置換された結合がアンチからゴーシュへと逆方向に回転した時、分子は2つの末端メチル基が近接するシクロペンタン様の配座を取る。結合が同一方向に回転するとすると、これは起こらない。2つの末端メチル基環のひずみエネルギーが、2つの似た、しかし非常に異なる配座間のエネルギー差の主な原因である。
アリルひずみ
[編集]
アリルひずみ(A1,3ひずみ)は、syn-ペンタンひずみと密接に関連している。アリルひずみの一例は2-ペンテンで見ることができる。オレフィンのエチル置換基は、オレフィンのビシナルメチル基と近接するように末端メチル基を回転することが可能である。これらの種類の化合物は通常、置換基間の立体ひずみを避けるためにより直線状の配座を取る[1]。
1,3-ジアキシアルひずみ
[編集]1.3-ジアキシアルひずみはsyn-ペンタンひずみと似た種類のひずみである。この場合、ひずみはシクロヘキサン環上の置換基('α')と、置換基の置換位置から2結合離れた2つのメチレン基(このため、1,3-ジアキシアル相互作用と呼ばれる)との間の立体ひずみによって起こる。置換基がアキシアル位の時、置換基はアキシアル位にあるγ水素原子と近づく。ひずみの量は置換基の大きさに大きく依存し、置換基がエクアトリアル位に位置する主要ないす形配座をとることによって解放することができる。配座間のエネルギー差はA値と呼ばれ、多くの異なる置換基についてよく知られている。A値は熱力学的パラメータであり、ギブズの自由エネルギー式を用いる手法に沿って元々測定された。一例として、シクロヘキサノン/シクロヘキサノールのアキシアル対エクアトリアル値(0.7 kcal/mol)の測定についてのメールワイン・ポンドルフ・バーレー還元/オッペナウアー酸化平衡がある[6]。
ねじれひずみ
[編集]ねじれひずみ(torsional strain)は結合のねじりに対する抵抗である。環状分子では、ピッツァーひずみとも呼ばれる。
ねじれひずみは、3結合によって隔てられてた原子がより安定なねじれ形配座の代わりに重なり形配座に置かれた時に起こる。エタンのねじれ形配座間の回転障壁は約2.9 kcal/molである[1]。当初は、この回転障壁はビシナル水素原子間の立体相互作用によるものであると考えられていたが、水素原子のファンデルワールス半径はこれが当てはまるには小さ過ぎる。近年の自然結合軌道(NBO)を用いた研究では、ねじれ形配座がより安定なのは超共役効果によるものであることが示されている[7]。ねじれ形配座から離れる回転はこの安定化力によって妨げられる。しかしながら超共役による説明は化学コミュニティーで多数派を占めている訳ではなく、分子軌道法[8]や原子価結合法[9]を用いた解析では依然、超共役ではなく(パウリの排他原理による)立体反発による寄与が支配的であるとされる。
ブタンといったより複雑な分子は2つ以上のねじれ形配座をとることができる。ブタンのアンチ配座はゴーシュ配座よりも約0.9 kcal/mol(3.8 kJ/mol)安定である[1]。これらのねじれ形配座はどちらも重なり形配座よりも安定である。エタンにおいて見られるような超共役効果の代わりに、ブタンにおけるひずみエネルギーはメチル基間の立体相互作用とこれらの相互作用によって引き起こされる角ひずみの両方が原因である。
環ひずみ
[編集]分子構造のVSEPR理論によれば、分子の望ましい幾何配置は結合性電子と非結合性電子が可能な限り離れるような配置である。分子において、これらの角度が最適値と比較して幾らか圧縮または拡張されることは非常にありふれたことである。このひずみは角ひずみまたはバイヤーひずみと呼ばれる[10]。角ひずみの最も単純な例はシクロプロパンやシクロブタンといった小さなシクロアルカンでる。そのうえ、解消することができない環形の重なり配座もしばしば存在する。
| 環の大きさ | ひずみエネルギー (kcal/mol) | 環の大きさ | ひずみエネルギー (kcal/mol) | |
|---|---|---|---|---|
| 3 | 27.5 | 10 | 12.4 | |
| 4 | 26.3 | 11 | 11.3 | |
| 5 | 6.2 | 12 | 4.1 | |
| 6 | 0.1 | 13 | 5.2 | |
| 7 | 6.2 | 14 | 1.9 | |
| 8 | 9.7 | 15 | 1.9 | |
| 9 | 12.6 | 16 | 2.0 |
原理上は、角ひずみは非環状化合物でも起こり得るが、この現象は希である。
小員環
[編集]シクロヘキサンはシクロアルカンにおける環ひずみを決定するための基準点と見なされており、ひずみがないかほとんど存在しないことが一般的に受け入れられている[1]。比較すると、より小さなシクロアルカンはひずみの増大によってエネルギー的により高い。シクロプロパンは三角形に似ており、ゆえにsp3混成炭素原子の望ましい109.5° よりもかなり小さい60° の結合角を持つ。そのうえ、シクロプロパンにおける水素原子は重なり形配座をとっている。シクロブタンは似たひずみを受け、約88° の結合角(完全に平面ではない)と重なり形水素原子を持つ。シクロプロパンおよびシクロブタンのひずみエネルギーはそれぞれ27.5および26.3 kcal/molである[1]。シクロペンタンが受けるひずみはかなり小さく、主に重なり形の水素原子からのねじれひずみによるものであり、ひずみエネルギーは6.2 kcal/molである。
渡環ひずみ
[編集]意外かもしれないが、中員環(7-13炭素)はシクロヘキサンよりも大きなひずみエネルギーを受ける。プレローグひずみとも呼ばれる渡環ひずみは、環状分子が角ひずみとねじれひずみを避けようと試みる時に起こる。その際に、向かい合った環上の置換基が近接し、ファンデルワールスひずみを受ける。
二環系
[編集]二環系におけるひずみエネルギー量は一般に、個々の環におけるひずみエネルギーの和である[1]。これは常に当てはまる訳ではなく、縮環することで追加のひずみが引き起こされることもある。
脚注
[編集]- ^ a b c d e f g h i j k l m Anslyn and Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006, ISBN 978-1-891389-31-3
- ^ Coxon and Norman, Principles of Organic Synthesis, 3rd ed., Blackie Academic & Pro., 1993, ISBN 978-0-7514-0126-4
- ^ Levine, Physical Chemistry, 5th ed., McGraw-Hill, 2002, ISBN 978-0-07-253495-5
- ^ Brown, Foote, and Iverson, Organic Chemistry, 4th ed., Brooks/Cole, 2005, ISBN 978-0-534-46773-9
- ^ Brown, H.C.; Johannesen, R.B. (1952). “Dissociation of the Addition Compounds of Trimethlboron with n-Butyl- and Neopentyldimethylamines; Interaction of Trimethylboron and Boron Trifluoride with highly hindered bases”. J. Am. Chem. Soc. 75: 16–20. doi:10.1021/ja01097a005.
- ^ Eliel, E. L., Wilen, S. H. (1994). The Stereochemistry of Organic Compounds. Wiley-Interscience. ISBN 978-0-471-01670-0
- ^ Weinhold, F. (2001). “Chemistry: A New Twist on Molecular Shape”. Nature 411 (6837): 539–541. doi:10.1038/35079225. PMID 11385553.
- ^ Bickelhaupt, F.M.; Baerends (2003). “The case for steric repulsion causing the staggered conformation of ethane.”. Angew. Chem. Int. Ed. 42: 4183–4188. doi:10.1002/anie.200350947.
- ^ Mo, Y.R. (2004). “The magnitude of hyperconjugation in ethane: A perspective from ab initio valence bond theory”. Angew. Chem. Int. Ed. 43: 1986–1990. doi:10.1002/anie.200352931.
- ^ Wiberg, K. (1986). “The Concept of Strain in Organic Chemistry”. Angew. Chem. Int. Ed. Engl. 25 (4): 312–322. doi:10.1002/anie.198603121.


