タットグラフ
| タットグラフ | |
|---|---|
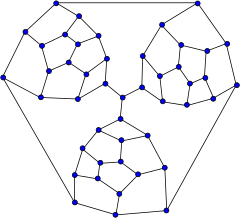 タットグラフ | |
| 命名者 | ウィリアム・トーマス・タット |
| 頂点 | 46 |
| 辺 | 69 |
| 半径 | 5 |
| 直径 | 8 |
| 内周 | 4 |
| 自己同型 | 3 (Z/3Z) |
| 彩色数 | 3 |
| 彩色指数 | 3 |
| 特性 |
立方体グラフ 平面グラフ 多面体グラフ |
タットグラフは、46頂点、69辺からなる3-正則グラフであり、W・T・タットにちなんで名付けられた[1]。頂点は3色で彩色可能、3-辺彩色可能であり、内周は4、半径は8である。
タットグラフは立方体グラフであり多面体グラフであるが、ハミルトン路を持たない。したがって、テイト予想の反例である[2]。
1946年にタットはこのテイト予想の反例としてこのグラフを公開した[3]。そして後に、グリンベルクの定理などにより、他の反例も見つかった。
構成
[編集]
タットは、タットの小片(Tutte fragment)と呼ばれるより小さな構成要素を3つ組み合わせることで、ハミルトン路を持たない多面体グラフを構成した。この小片の飛び出たような辺は「強制的な」辺(=ハミルトン路の一部に使わなければならない辺)であり、この辺を中心の頂点で3つ連結すると、ハミルトン路はその3つの辺の内2つしか通る事ができない。したがって、タットグラフはハミルトン路を持たない。
組み合わせたグラフは3-正則グラフであり、平面グラフである。したがって、シュタイニッツの定理より、対応する多面体が存在し、その多面体は25個の面を持つ。
この多面体は、四面体から3つの頂点を切り落とすことで幾何学的に実現することができる。4つの大きな面を含む9面からなり、4面のそのうち3つは小片の間に対応し、4つ目は外周に対応する。
代数的な性質
[編集]タットグラフの自己同型群は Z/3Z であり、3つの元を持つ巡回群である。
タットグラフの固有多項式は
である。
関連するグラフ
[編集]タットグラフは1946年に発見された3-正則グラフであり、最初にハミルトン路が存在しないことが知られたグラフであるが、そのような性質を持つグラフの中で最小のグラフではない。
1965年にレーダーバーグは38頂点の Barnette–Bosák–Lederberg グラフを発見した[4][5]。1968年には、グリンベルクがテイト予想の反例として42、44、46頂点のグリンベルクグラフを追加した[6]。1974年には、フォークナーとヤンガーは42頂点と44頂点の反例を発見した[7]。
そして1988年に、ホルトンとマッケイは6種類の38頂点からなるハミルトン路を持たない多面体を見つけた。それらは五角柱の2つの頂点をタットの小片に置き換えたものからなる[8]。
出展
[編集]- ^ Weisstein, Eric W. "Tutte's Graph". MathWorld.
- ^ Tait, P. G. (1884), “Listing's Topologie”, Philosophical Magazine, 5th Series 17: 30–46. Reprinted in Scientific Papers, Vol. II, pp. 85–98.
- ^ Tutte, W. T. (1946), “On Hamiltonian circuits”, Journal of the London Mathematical Society 21 (2): 98–101, doi:10.1112/jlms/s1-21.2.98.
- ^ Lederberg, J. "DENDRAL-64: A System for Computer Construction, Enumeration and Notation of Organic Molecules as Tree Structures and Cyclic Graphs. Part II. Topology of Cyclic Graphs." Interim Report to the National Aeronautics and Space Administration. Grant NsG 81-60. December 15, 1965. [1].
- ^ Weisstein, Eric W. "Barnette-Bosák-Lederberg Graph". MathWorld.
- ^ Grinberg, E. J. "Plane Homogeneous Graphs of Degree Three without Hamiltonian Circuits." Latvian Math. Yearbook, Izdat. Zinatne, Riga 4, 51–58, 1968.
- ^ Faulkner, G. B. and Younger, D. H. "Non-Hamiltonian Cubic Planar Maps." Discrete Math. 7, 67–74, 1974.
- ^ Holton, D. A.; McKay, B. D. (1988), “The smallest non-Hamiltonian 3-connected cubic planar graphs have 38 vertices”, Journal of Combinatorial Theory, Series B 45 (3): 305–319, doi:10.1016/0095-8956(88)90075-5.


