バンド図

平衡状態におけるpn接合のバンド図。
緑の線が伝導帯端、赤い線が価電子帯端、点線がフェルミ準位である。緑の線と赤い線の間が禁制帯である。
空乏層は薄い色で塗られた部分である。φ_Bは、正孔のレベルと電子のレベルに対するバンドシフトを意味する。

LEDの内部動作。回路（上）とバイアス電圧が印加されたときのバンド図（下）を示す。

平衡状態におけるショットキー障壁のバンド図

平衡状態における半導体ヘテロ接合のバンド図

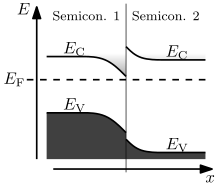
半導体の固体物理学において、バンド図（バンドず、英語: Band diagram）は、空間次元（xと表記されることが多い）の関数として様々な鍵となる電子エネルギー準位（フェルミ準位と近くのエネルギーバンド端）を描画した図である。バンド図は、半導体デバイスの多くの種類の動作を説明するのに役立つ、そして、位置によってどのようにバンドが変化するのか（バンドベンディング）を視覚化するのにも役立つ。バンドはエネルギーレベルの充填を区別するために着色されることがある。

バンド図は、バンド構造図と混同するべきではない。バンド図とバンド構造図の縦軸は、ともに電子のエネルギーである。異なる点は、バンド構造図の横軸が無限大で均一な物質（結晶あるいは真空）における電子の波数ベクトルを表現していることである。一方でバンド図の横軸は、複数の物質を通した空間の中の位置を表現している。

バンド図は、場所から場所へのバンド構造の「変化」を示すので、バンド図の解像度は、不確定性原理によって制限される。つまり、バンド構造は運動量に依存しており、運動量は大きな長さのスケールに対してのみ正確に定義される（運動量＝波数ベクトル×ディラック定数なので、位置が不確定になる）。このため、バンド図は長いスケールのバンド構造の変化を正確に描画することしかできず、異なる物質間（あるいは物質と真空の間）の境界面の鮮明かつ原子スケールの顕微鏡写真のようなものを見せることは困難である。

一般的に長い距離の影響は、漸近的なバンドベンディング（バンドの変化）としてバンド図の中に示すことができるが、境界面は「ブラックボックス」として描画しないといけない。

詳細

バンド図の縦軸は、電子エネルギーを表現しており、そのエネルギーは運動エネルギーとポテンシャルエネルギーを含んでいる。横軸は位置を表現しており、目盛りは描かれないことが多い。バンド図は、エネルギーバンドを示しているので、不確定性原理によって高い位置解像度でバンド図を描画することができないことに注意するべきである（バンド構造は運動量に依存するので、位置が不確定になる）。

基本的なバンド図は、電子エネルギーレベルだけを示すが、バンド図はより多くの機能で装飾されることも多い。電子が光源によって励起されたり、励起状態から緩和するとき、流れるように電子（あるいは、正孔）のエネルギーと位置の動きを漫画のように描くことがよく見受けられる。バンド図は、どのようにバイアス電圧が印加されているのか、どのように電荷が流れているのかなどを示すために回路図と接続されているように描かれることもある。バンドは、エネルギーレベルの充填を示すために着色されることがある。あるいは、バンドギャップが代わりに着色されることも時々ある。

エネルギー準位

物質と要求される詳細度によって、各種エネルギー準位が位置に対して描画される。

• E_F または μ: バンドの数量ではないが、フェルミ準位（合計化学ポテンシャル）は、バンド図の重要なレベルである。フェルミ準位は、デバイスの電極によって設定される。平衡状態におけるデバイスに対して、フェルミ準位は一定であるので、水平線としてバンド図に描かれる。平衡状態以外（例えば、電位差が印加されているとき）、フェルミ準位は水平ではない。そのうえ、平衡状態ではない半導体において、異なるエネルギーバンドに対して複数の擬フェルミ準位を示す必要があるかもしれない。ところが、非平衡状態の絶縁体または真空において、準平衡状態を説明できない可能性があり、フェルミ準位を定義できない。
• E_C: 伝導帯端（conduction band edge）は、状況に応じて示されるべきである。n型半導体のように電子は伝導帯の底で転送されている可能性がある。伝導帯端は、バンドベンディング効果を単純に説明するために絶縁体の中でも示されるかもしれない。
• E_V: 価電子帯端（valence band edge）も同様に状況に応じて示されるべきである。p型半導体のように電子（あるいは正孔）は価電子帯の最上部を通って転送されている。
• E_i: 真性フェルミ準位（intrinsic Fermi level）は、半導体の中に描かれるかもしれない。どの位置でフェルミ準位が中性的にドーピングされた物質（すなわち可動電子と正孔の数が等しい）になるのかを示す。
• E_imp: 不純物エネルギー準位（impurity energy level）。多くの格子欠陥とドーパント（不純物）が半導体あるいは絶縁体のバンドギャップの内部に状態を追加する。それらのエネルギー準位を描画することは、イオン化されているかどうかを見るために役に立つ。
• E_vac: 真空において、真空準位（vacuum level）は、エネルギー $-e\phi$ を示す。ここで $\phi$ は、電位である。真空は、伝導帯端の役割を演じる E_vac を伴った絶縁体の一種と考えることができる。真空と物質の境界面において、真空のエネルギーは、その物質の仕事関数とフェルミ準位の合計によって定まる。
• 電子親和力準位（Electron affinity level）: 時折、「真空準位」が物質内部にすら描かれることがある。電子親和力によって決定される伝導帯の上の固定された高さに描かれる。この「真空準位」は、あらゆる実際のエネルギーバンドと一致せず、定義は曖昧である（厳密に言えば、電子親和力は表面の特性であり、塊の特性ではない）。しかしながら、アンダーソンの法則あるいはショットキー＝モット則のような近似の利用において役立つガイドとなるかもしれない。

バンドベンディング

→詳細は「バンドベンディング」を参照

バンド図を見たとき、物質中の電子エネルギー準位（バンド）は、接合部近傍で上や下に曲がることができることに気が付く。この効果はバンドベンディング（Band bending）として知られている。それはあらゆる物理的（空間的）な曲がり（ベンディング）とは一致しない。むしろ、バンドベンディングは、空間電荷効果の影響による接合部付近の半導体のバンド構造のエネルギーオフセットにおける電子的構造の局所的な変化とされる。

半導体の中のバンドベンディングの基礎となる主要原理は、空間電荷である。つまり、電荷中性における局所的な不均衡である。ポアソン方程式は、バンドに曲線を与える。バンドのどこにでも電荷中性における不均衡がある。電荷不均衡の理由は、均一な物質はどこでも電荷中性（均一な物質は平均的に電荷中性でないといけない）であるが、境界面にそのような要求は存在しないからである。

次のように理由は異なるが、事実上、全ての種類の境界面は、電荷不均衡を起こす。

• 2つの異なる型の同じ材質の半導体の接合（例えば、pn接合）において、ドーパントは低密度に分布しており、半導体のシステムに摂動を与えるだけなので、バンドは連続的に変化する。
• 2つの異なる材質の半導体の接合（ヘテロ接合）において、ある物質から他の物質へバンドエネルギーが鋭く変化している。接合におけるバンドの配置（伝導帯エネルギーの違い）は、固定されている。
• 半導体と金属の接合において、半導体のバンドは、金属のフェルミ準位にピン留めされたようになっている（金属半導体接合#ショットキー＝モット則とフェルミ準位のピン止めを参照）。
• 導体と真空の接合において、真空準位（真空の静電ポテンシャルに基づく）は、金属の仕事関数とフェルミ準位によって定められる。このことは、絶縁体から導体への接合にも（通常は）適用される。

接触部に2つの異なる種類の物質があるとき、バンドがどのように曲げられるのかを知ることは、接合が整流（ショットキー接触）あるいはオーム性抵抗（オーミック接触）のどちらになるのかを理解する鍵となる。バンドベンディングの度合いは、相対的なフェルミ準位と接合部を形成する物質の電荷キャリア密度に依存する。n型半導体において、バンドは上に曲がる。一方でp型において、バンドは下に曲がる。 バンドベンディングは、磁場あるいは温度勾配のどちらにも依存しない。むしろ、バンドベンディングは、電場の力だけで生じる。

参考文献

• James D. Livingston, Electronic Properties of Engineering Materials, Wiley (December 21, 1999).

関連項目

• アンダーソンの法則 - 真空の電子親和力に基づくヘテロ接合のバンド配置に関する近似法則
• ショットキー＝モット則 - 真空の電子親和力と仕事関数に基づく金属半導体接合のバンド配置に関する近似法則
• 電界効果 - バンドベンディングは、半導体表面の真空（あるいは絶縁体）における電場によって誘導される。
• トーマス・フェルミ遮蔽 - 荷電欠陥の周囲に生じるバンドベンディングの基本理論
• 量子静電容量 - 二次元電子ガスを含む物質系に対する電界効果におけるバンドベンディングの特殊な事例