フィゾーの実験

フィゾーの実験で用いられた実験装置

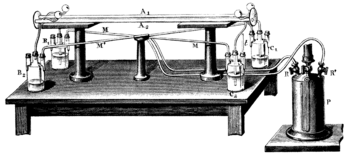
フィゾーの実験（フィゾーのじっけん）はアルマン・フィゾーにより1851年に行われた、動く水の中を光が伝わる速度を測る実験である。フィゾーは特別な配置の干渉計を考案し、媒体の運動が光の速度に与える影響を測定した。

当時一般的だった理論によれば、移動する媒体中の光の速度は媒体によって引きずられ、測定される光の速度は「媒体中の光速度」に「媒体そのものの速度」を単に加えたものになるとされていた。実際にフィゾーは引きずりの効果を検知したのであるが、その効果の大きさ（光速度への影響）は上の予想に比べ大分小さいものであった。フィゾーの測定結果は一見（理論的には問題があると考えられていた）フレネルによるエーテルの部分的引きずり仮説を支持するようにうつり、そのため多くの物理学者を悩ませることになる。フィゾーの実験の予期されなかった結果が満足に説明されるには半世紀以上を経たアインシュタインの特殊相対性理論の登場を待たねばならなかった。後年アインシュタインは特殊相対論に至るまでの考察に重要であった実験的結果の一つとしてフィゾーの実験を挙げている。フィゾーの実験結果は特殊相対論の速度の加法則（の特別な場合）に対応する。

なお、本項で説明するフィゾーの実験は英語でthe Fizeau experimentと呼ばれるほど際立って有名なものである（英語の冠詞も参照）が、フィゾーは精力的な実験家であり他にも様々な状況での光速度を測定する多くの実験を実施している。

実験のセットアップ(構成、諸条件)

フィゾーの実験(1851)のセットアップ

光源S′から発せられる光線はビームスプリッターGにより反射しレンズLによりコリメートされ平行光線になる。スリットO₁とO₂を通過した2つの光線は管A₁とA₂を通るのだが、それぞれの管の中には矢印で示されるように逆方向に水が流れている。2つの光線はレンズL′の焦点に置かれた鏡mで反射する。そのため片方の光線は管を通過する際に常に水流と同じ方向に伝わり、もう片方の光線は常に水流とは逆の方向に伝わるのである。管の中を往復した二つの光線はSで再び交わる(recombine)。そこで作られる干渉縞は図示されている接眼レンズにより観察できる。干渉縞の解析により水流に沿う光と逆行する光の速度差が計測できるのである。

フレネルの引きずり係数

管の中を流れる水の速度をvとする。非相対論的な（光の媒体としての）エーテル仮説によれば光速度は水の流れに沿って「引きずられる」場合は増加し、水の流れに「逆らう」場合は減少する。光の伝わる速度は全体として媒体中の光速度に水の速度を加えたものになるはずである。

すなわち、nを水の屈折率とすると静水中の光速度はc/nになる。上の議論によれば実験装置の経路を通る光速度wは、片方の経路については

$w_{+}={\frac {c}{n}}+v$

となりもう片方については

$w_{-}={\frac {c}{n}}-v$

となる。水の流れに逆らう方向に進む光は沿う方向に進む光に比べ遅くなっている。

2つの光線を再び合流させ生ずる干渉縞の様相は2つの光線が経路をたどるのにかかる時間差に依存する。それにより、光速度が水の速度にどのように依存するかが測れるのである。

この観測によりフィゾーは

$w_{+}={\frac {c}{n}}+v\left(1-{\frac {1}{n^{2}}}\right)$

という関係式を見出した。光は実際水によって引きずられている。しかし引きずりの大きさは予測されたものよりも大分小さいのである（水の屈折率n=1.33から $\left(1-{\frac {1}{n^{2}}}\right)=0.44$ となる）。

フィゾーの実験結果を受け、物理学者たちはフレネルの仮説が実験的には正しいことを認めざるを得なかった。フレネルの仮説はフランソワ・アラゴによる1810年に行なわれた実験の結果を説明するため1818年に提案されたもので、静的なエーテル中を媒質が動く場合、媒質中の光は媒質の速度の「一部だけ」引きずられるとされる。この割合を表す引きずり係数fは

$f=\left(1-{\frac {1}{n^{2}}}\right)$

である。しかしこの仮説は理論的に満足のいくものではなく、様々な問題点が指摘されていた。

1895年、ヘンドリック・ローレンツは光の分散の効果を取り入れるとフレネルの引きずり係数には補正項

$w_{+}={\frac {c}{n}}+v\left(1-{\frac {1}{n^{2}}}-{\frac {\lambda }{n}}\cdot {\frac {\mathrm {d} n}{\mathrm {d} \lambda }}\right)$

がつくはずだとした。

後にフレネルの引きずり係数は相対論的な速度の加法則から従うことが示される。

→詳細は「§ 特殊相対論での実験結果の理解」を参照

追試

マイケルソンとモーリーにより改良版フィゾーの実験(1886年)光源aからのコリメートされた光はビーム・スプリッターbによって二つに分けられる。一つは経路b c d e f b gを通り、もう一つは経路b f e d c b gを通る。

1886年にアルバート・マイケルソンとエドワード・モーリーはフィゾーの実験をより良い精度で再実施した。彼等の実験ではフィゾーの元々の実験にあった問題について対策がたてられていた。問題とは以下のものである。

1. フィゾーの装置では、二つの光路（光の伝わる経路）が厳密に一致しない場合、光学系（optical component、実験装置で光が通る部分）に歪みや温度差、圧力差が生じると干渉縞が本来観測したい効果によらないずれを示してしまう。
2. 観測にかけられる時間が短い。圧力をかけて作られた水流が長時間は保たないからである。
3. フィゾーの用いた管は細く、管の中の層流の配位（水流の速度が管の中心からの距離に依存してしまうこと）を考慮に入れると、実験で使えるのは管の中心部分のみである。そのため干渉縞は薄いものになってしまう。
4. フィゾーは管の中心部分での流れの速度を管全体を通る水の流束から見積っているが、その評価には不定性がある。

マイケルソンはフィゾーの装置を設計しなおし、より太い管を使うようにし、より大きい水の貯蔵器を使って一定の速度の水流が3分間も保つようにした。またマイケルソンは装置を共通光路干渉計として設計したため、光学系の歪みや圧力、温度の揺らぎなどで光路の長さがかわっても干渉縞には影響せず、光学系のアラインメントがとれた瞬間（すなわち種々の装置の向きを正しく合わせられた瞬間）に白色の干渉縞が見えるようになっていた。装置の配置から言うと光路はサニャック干渉計と同じであり、各々の光路上で光は偶数回反射される。結果として得られる干渉縞は極めて安定しており、光学系の一部を移動させても一次近似では干渉縞に変化は起きない。実際にhにガラス板を挿入させたり、光路に火のついたマッチをかざしたりしてさえも干渉縞の中心がずれない程であった。この装置による追試によりマイケルソンとモーリーはフィゾーの結果を完全に確認することに成功した。

1914年から1915年にかけてはピーター・ゼーマンによる一連の実験が行なわれた。マイケルソンの装置をスケール・アップさせた（形状、機能などはそのままにサイズを大きくさせた）実験装置はアムステルダムの主水道管に直接つながれていた。ゼーマンは紫（波長4358 Å）から赤(6870 Å)の単色光をつかって観測を行いローレンツによる補正項まで検証することに成功した。1910年にはen:Franz Harressは「回転する」装置を用いた。実験結果は全体としてはフレネルの引きずり係数の存在を確認したのであるが、しかし、データには「系統的な偏り(systematic bias)」があったと報告されている。後年この偏りはサニャック効果として理解できることが判明した。

それ以降、（多くの場合はサニャック効果も含めて）引きずり係数の測定のため多くの実験が行われた。例えばリングレーザーと回転円板を用いたものや中性子干渉計によるものがある。また媒体が光と直行方向に移動する場合の（transverseな）引きずり効果も観測されている。

実験結果をめぐる科学的議論

フレネルの仮説はフィゾーの実験結果を説明することには成功したものの、フィゾー自身を含め（1851年）、マスカール（1872年）、Ketteler（1873年）、Veltmann（1873年）、ローレンツ（1886年）などこの分野の多くの指導的な専門家は、フレネルの部分エーテル引きずり仮説が理論的には根拠の薄いものだという見解で一致していた。例えば、Veltmann（1870年）はフレネルの式は（屈折率が波長に依存するため）光の波長に応じてエーテルの引きずられる割り合いが変化せねばならぬことを指摘した。同様にマスカール（1872年）は複屈折を示す物質では異なる偏光を持つ光についてエーテルの引きずられる割り合いが異なることを指摘した。エーテルは同時に（異なる引きずり係数に対応する）異なる運動状態にあるという考えにくい性質を持つことになってしまっているのである。

フィゾーが自分自身の実験結果に満足していなかったことは論文の結論部分から容易にみてとれる。

The success of the experiment seems to me to render the adoption of Fresnel's hypothesis necessary, or at least the law which he found for the expression of the alteration of the velocity of light by the effect of motion of a body; for although that law being found true may be a very strong proof in favour of the hypothesis of which it is only a consequence, perhaps the conception of Fresnel may appear so extraordinary, and in some respects so difficult, to admit, that other proofs and a profound examination on the part of geometricians will still be necessary before adopting it as an expression of the real facts of the case.（訳：実験の成功によりフレネルの仮説を、少なくとも光速度への媒体の運動の影響に関するフレネルによる表式を、採用するより他なくなったように私には思われる。フレネルの表式はフレネルの引きずり仮説の一つの帰結に過ぎないわけだが、表式の正しさは確かに仮説が正しいことをも示す強い証拠ではあろう。しかし、フレネルの仮説はあまりにも奇抜(extraordinary)なものであり、その正しさを認めることはある意味非常に難しいと言ってもよかろう。そのため、フレネルの部分引きずり仮説が実際に起っている現象の表現として適切であるとするには、他の証拠や幾何学者(理論家)による深い吟味が今後必要であろう。）

殆どの物理学者はフレネルの部分エーテル引きずり仮説に満足していなかったにもかかわらず、フィゾーの結果はその後、追試や精度をあげた再実験により（前節参照）高い精度で検証されていくのである。

さらに新たな大きな問題が1887年のマイケルソン・モーリーの実験により生じた。部分エーテル引きずり仮説によればエーテルは殆ど静止していなければならない。これは、マイケルソン・モーリーの実験でエーテルと地球の相対速度（いわゆるエーテルの風）が検出されるべきことを意味するのだが、実験結果は否定的なものであった。当時エーテル説の観点からは種々の実験によって得られた結果は互いに矛盾してしまっていたのである。光行差とフィゾーの実験（とその追試）は部分エーテル引きずり仮説を支持する一方、1887年のマイケルソン・モーリーの実験はエーテルが地球に対して静止していること、すなわちエーテルが（部分的ではなく）完全に引きずられていること(エーテル引きずり仮説参照)を示していた。フレネルの仮説がフィゾーの実験結果を説明する、正にその事実が理論的な危機を生んでいたと言える。この危機的状況が解決されるには特殊相対論の登場を待たねばならなかった。

ローレンツによる解釈

→詳細はローレンツのエーテル理論とローレンツ変換の歴史を参照

1892年ヘンドリック・ローレンツはフレネルの模型を修正し、エーテルが完全に静止しているような理論を提案した。ローレンツの模型ではフレネルの引きずり係数は移動する水と静止した（すなわち引きずられない）エーテルとの相互作用から従う。またローレンツは二つの慣性系(reference frame)の間の変換が補助的な時間座標

$t^{\prime }=t-{\frac {vx}{c^{2}}}$

を導入すると簡単になることを見出し、この時間座標を局所時間(local time)と名付けた。

1895年ローレンツは局所時間の概念をもとにより一般的にフレネルの係数を導出した。しかしながら、ローレンツの理論にはフレネルの理論にあるのと同じ基本的な問題がある。すなわち、静的なエーテルはマイケルソン・モーリーの実験と矛盾するのである。この問題を解決するため1892年にローレンツは移動する物体は運動の方向に関して収縮をおこす（ローレンツ収縮、ジョージ・フィッツジェラルドが1889年に既に同様の結論に逹していたためフィッツジェラルド=ローレンツ収縮とも呼ばれる）という仮説を提唱した。1904年にいたるまで、ローレンツはこれらの局所時間、ローレンツ収縮を表す数式についての研究を続けた。これらの表式はローレンツの名を冠し今日ローレンツ変換と呼ばれている。ローレンツ変換の表式は後に第一原理からアインシュタインが導いたものと数式的には一致している。しかし、アインシュタインの導出とは異なりローレンツの議論はアドホックなもの、すなわち深い原理に基づかず、問題を表面的にその場限りに解決するためのものであった。

特殊相対論での実験結果の理解

→詳細は「特殊相対性理論」を参照

アインシュタインは論文『運動物体の電気力学について』で、ローレンツ変換がたった二つの簡単な原理（相対性原理と光速度不変性）の論理的な帰結として理解できることを示した。さらにアインシュタインは特殊相対論の立場では静的なエーテルという概念は全く必要のないものであり、ローレンツ変換は時間と空間そのものの性質であることを見抜いていた。

アインシュタインが相対論に至った考察において、運動する磁石と導体・エーテルの風を否定する実験・光行差とならんでフィゾーの実験は鍵となる実験結果であった。ロバート・シャンクランドはアインシュタインが会話のなかでフィゾーの実験の重要性を強調したことを記録にのこしている。

He continued to say the experimental results which had influenced him most were the observations of stellar aberration and Fizeau's measurements on the speed of light in moving water. "They were enough," he said.（訳：アインシュタインは続いて彼が最も影響を受けた実験結果は光行差とフィゾーによる運動する水の中の光速度の測定だったとした。「それで十分だった」とアインシュタインは言った。）

マックス・フォン・ラウエは1907年にフレネルの引きずり係数は相対論的な速度の加法則の自然な帰結として簡明に理解できることを見出した。すなわち、

静止した水の中を伝わる光の速度はc/nである。

相対論的な速度の加法則によれば実験室中を水が速度vで流れる場合、実験室で観測される光の速度は（光と水が同じ方向だとして）

$V_{\mathrm {lab} }={\frac {{\frac {c}{n}}+v}{1+{\frac {{\frac {c}{n}}v}{c^{2}}}}}={\frac {{\frac {c}{n}}+v}{1+{\frac {v}{cn}}}}$

で与えられる。従って速度差は、（vがcに比べ小さいとしてv/cの高次項を無視して）、

$V_{\mathrm {lab} }-{\frac {c}{n}}={\frac {{\frac {c}{n}}+v}{1+{\frac {v}{cn}}}}-{\frac {c}{n}}={\frac {{\frac {c}{n}}+v-{\frac {c}{n}}(1+{\frac {v}{cn}})}{1+{\frac {v}{cn}}}}={\frac {v\left(1-{\frac {1}{n^{2}}}\right)}{1+{\frac {v}{cn}}}}\approx v\left(1-{\frac {1}{n^{2}}}\right)$

となる。この式が正しいのは、v/c ≪ 1が満たされる場合だが、フィゾーの実験条件は実際にこの条件を満足している。そして式は正しくフィゾーの実験結果を再現しているのである。

このようにフィゾーの実験はアインシュタインの速度の加法則（の速度の方向が同じ場合）を裏付ける結果になっている。

関連項目

• 光の波動説
• 特殊相対論の検証
• エーテル引きずり仮説
• 特殊相対論の歴史

外部リンク

• 日本大百科全書(ニッポニカ)『フィゾーの実験』 - コトバンク