フォークマングラフ

フォークマングラフ
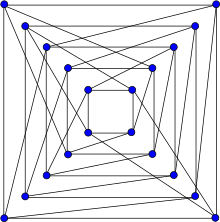フォークマングラフ
命名者	ジョン・フォークマン
頂点	20
辺	40
半径	3
直径	4
内周	4
彩色数	2
彩色指数	4
特性	ハミルトン 正則 2部 半対称 オイラー パーフェクト

数学のグラフ理論の分野におけるフォークマングラフ（英: Folkman graph）とは、ジョン・フォークマンの名にちなむグラフであり、20個の頂点と40個の辺を持ち、4-正則な2部グラフである。

フォークマングラフはハミルトンであり、彩色数は 2、彩色指数は 4、半径は 3、直径は 4、内周は 4 である。4-頂点連結かつ 4-辺連結なパーフェクトグラフでもある。

代数的性質

フォークマングラフの自己同型群は、その辺上では推移的に作用するが、頂点上ではそのように作用しない。フォークマングラフは、辺推移的かつ正則な最小の無向グラフであるが、頂点推移的ではない。そのようなグラフは半対称グラフと呼ばれ、1967 年にこのグラフを発見したフォークマンによって初めて研究された。

半対称グラフとしてのフォークマングラフは2部グラフであり、その自己同型群は各二つの頂点からなる bipartition の集合上で推移的に作用する。フォークマングラフの彩色数を示している下の図においては、緑の頂点が赤の頂点へと写される自己同型は存在しないが、どのような赤の頂点も他の赤の頂点へと写すことができ、また、どのような緑の頂点も他の緑の頂点へと写すことが出来る。

フォークマングラフの特性多項式は $(x-4)x^{10}(x+4)(x^{2}-6)^{4}$ である。

ギャラリー

• 
  フォークマングラフの彩色指数は 4 である。
• 
  フォークマングラフの彩色数は 2 である。
• 
  フォークマングラフはハミルトンである。