ホイヘンス=フレネルの原理

ホイヘンス゠フレネルの原理(ホイヘンスフレネルのげんり、英: Huygens–Fresnel principle)[1]、または単にホイヘンスの原理(ホイヘンスのげんり、英: Huygens' principle)は、波動の伝播問題(遠方場の極限や近傍場の回折)を解析する手法である。ホイヘンス゠フレネルの原理によると、前進波の波面の各点が二次波とよばれる新しい波の波源となり、全体としての前進波は(既に伝播した媒質から生じる)全ての二次波を重ね合わせたものとなる。この波の伝播の考え方は回折のような様々な波動現象の理解を助ける。
例えば、2つの部屋が開いた出入口のみで繋がっており、一方の離れた部屋の角で音が鳴ったとする。するともう一方の部屋にいる人には出入口の所で音が鳴ったように聞こえる。2つ目の部屋のみを考えると、出入口の地点での振動する空気は音源である。障害物の端を通る光にも同じことがいえるが、可視光は波長が短いために観測が難しい。
ホイヘンス゠フレネルの原理は1678年にオランダの物理学者クリスティアーン・ホイヘンスが元となるホイヘンスの原理を発見し、1690年に著書"Traite de la lumiere"に記した[2]。オリジナルのホイヘンスの原理では後進波が存在しないことを説明できなかったが、フランスの物理学者オーギュスタン・ジャン・フレネルが1836年に修正を加えてこの問題点を解決した。その後1882年にグスタフ・キルヒホフがヘルムホルツ方程式を基礎としたフレネル゠キルヒホフの回折理論にて理論的な説明を与えた。
ホイヘンスの原理
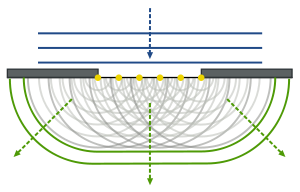
[編集]オリジナルのホイヘンスの原理では、伝播する波動の次の瞬間の波面の形状を考える時、波面のそれぞれの点から球面状の二次波(素元波)が出ていると考える。この二次波の包絡面が次の瞬間の新たな波面となる。
ホイヘンスの原理は直感的に回折の現象をうまく説明できる。しかし、厳密な回折の計算を行う時、フレネル回折の式から回折現象は干渉の一部であるとみなされるようになった。またあくまで直感的なものであったので、「波の進行方向の後ろの素元波の包絡線に、なぜ次の波面(後進波)ができないのか?」などのホイヘンス自身にも説明できない問題点があった。
この問題点は後にオーギュスタン・ジャン・フレネルが二次波の干渉(重ね合わせ)を考慮することで解決した。現在では単に「ホイヘンスの原理」というと、この問題点を解決したホイヘンス゠フレネルの原理を指すことが多い。
単スリット回折
[編集]ホイヘンスの原理の一般的な応用は、平面波(光、ラジオ波、X線や電子線など)が任意の絞りを通過する場合である。ホイヘンスの原理によれば、穴のそれぞれの点が点源として働き、点源からは全ての方向に球面状に光が広がる。絞り上の全ての点源からの波の和が積分モデルや数値モデルで計算される。
単スリット回折を考える。単スリットを通して離れたスクリーンへ光を照射する。ここでスクリーン上のどの地点に暗い縞が現れるかを計算しよう。次にこの幅広いスリットをより多くの狭いスリット(サブスリット)で置き換え、それぞれのスリットによって生成される波を加える。2つの小さなスリットの場合には光路がだけ異なる場合に(位相が180°異なり)干渉して弱め合う。3つのスリットによる3つの波の場合についても位相ベクトルやそれに似た波の重ね合わせの計算により、位相が120°だけ異なるときに打ち消し合い、よってスクリーン上の点とスリットの光路差はだけ異ならなければならない。4つのスリットの場合も同様である。1つの幅広いスリットを無限のサブスリットで近似する極限では、スリットの端からの光路差が正確にだけ異なる場合に干渉して完全に打ち消し合う(よってスクリーンには暗い縞が現れる)。
原理の数学的表現
[編集]
P0は光源、周波数はf。複素振幅はU0で表記する。起こされる球面波の波長はλ、波数はk = 2π/λ。
大きさは移動距離に反比例して減少し、位相は移動距離のk倍として変化することだ。重ね合わせの原理により、二次波の寄与によるPでの複素振幅は、次式で与えられる。[3]
Sは球の表面を表し、sはQとPの間の距離である。χは一次波面の法線と二次波面の法線の間の角度である。
単一の膨張球面波からなる開口照明の場合、波の曲率半径が十分に大きければ、キルヒホッフはK(χ)について次の式を与えた。
任意の照明は点光源の集まりに分解することができ、波動方程式の線形性を利用して各点光源に個別に原理を適用することができる。K(χ)は一般に次のように表すことができる:
関連項目
[編集]| 物理学 |
|---|
| ウィキポータル 物理学 執筆依頼・加筆依頼 |
 |
| ウィキプロジェクト 物理学 |
| カテゴリ 物理学 |
- グリーン関数
- グリーンの定理
- グリーンの恒等式
- フレネル回折 - 近傍場の回折パターン
- フラウンホーファー回折 - 遠方場の回折パターン
- 二重スリット実験
- ナイフエッジ効果
- フェルマーの原理
- フーリエ光学
- 屈折
- 反射
- フェーズドアレイレーダー
脚注
[編集]- ^ Longhurst RS, Geometrical and Physical Optics, 2nd Edition, 1968, Longmans [London]
- ^ 1911 Encyclopedia Britannica 11th edition
- ^ J. Goodman (2005). Introduction to Fourier Optics (3rd ed.). Roberts & Co Publishers. ISBN 978-0-9747077-2-3







