マギーグラフ
| マギーグラフ | |
|---|---|
 | |
| 命名者 | W. F. McGee |
| 頂点 | 24 |
| 辺 | 36 |
| 半径 | 4 |
| 直径 | 4[1] |
| 内周 | 7[1] |
| 自己同型 | 32[1] |
| 彩色数 | 3[1] |
| 彩色指数 | 3[1] |
| 特性 |
立方体グラフ ケージ ハミルトングラフ |
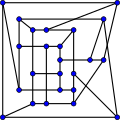
マギーグラフとは、グラフ理論のグラフの1つであり、24頂点、36辺の、3-正則グラフである[1]。(3-7)-ケージ とも呼ばれる。
マギーグラフは (3,7)-ケージの唯一の例であり、 内周が7である立方体グラフの最小の例である。また、立方体グラフかつケージで、ムーアグラフではない最小のグラフである。
Sachsがマギーグラフを最初に見つけたが、発表しなかった[2]。その結果、1960年に発表したマギーにちなんで、このグラフはマギーグラフと名付けられた[3]。その後、1966年にウィリアム・トーマス・タットにより、マギーグラフは (3,7)-ケージの唯一の例であることが証明された[4][5][6]。
マギーグラフは平面グラフにすると8箇所以上で交叉する。つまり、マギーグラフの交叉数_(グラフ理論)は8である。交叉数が8となる最小な立方体グラフには5つの非同型なグラフがあり、マギーグラフはその1つである。一般化ピーターセングラフ(ナウルグラフ)もその1つであるG(12,5)[7][8]。
マギーグラフの距離は 4、直径は 4、彩色数は 3 、彩色指数は 3である。マギーグラフは 3-頂点連結グラフ であり 3-辺連結グラフである。 本型埋め込み((book embedding)の厚み(book thickness)は 3 であり、queue numberは 2である[9]。
代数的性質
[編集]マギーグラフの特性多項式はである。 マギーグラフの自己同型群の位数は 32 であり、その頂点は推移的ではない。つまり、長さ8や16の2つの頂点軌道をもつ。マギーグラフはvertex-transitive graphではない(頂点が推移的でない)最小の立方体グラフである[10]・
ギャラリー
[編集]-
マギーグラフの交叉数は8
-
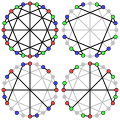
マギーグラフの彩色数は3
-
マギーグラフの彩色指数は3である
-
マギーグラフの非循環彩色数は3である
-
マギーグラフの他の表現
注釈・出典
[編集]- ^ a b c d e f Weisstein, Eric W. "McGee Graph". mathworld.wolfram.com (英語).
- ^ Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
- ^ McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960
- ^ Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
- ^ Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982
- ^ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
- ^ Sloane, N.J.A. (ed.). "Sequence A110507 (Number of nodes in the smallest cubic graph with crossing number n)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
{{cite web}}: Cite webテンプレートでは|access-date=引数が必須です。 (説明) - ^ Pegg, E. T.; Exoo, G. (2009), “Crossing number graphs”, Mathematica Journal 11.
- ^ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ^ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.