ユークリッドの果樹園
表示
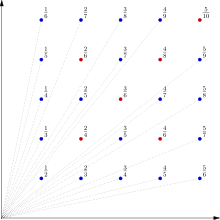
ユークリッドの果樹園は、第一象限に正方格子状に植えられた、単位高さの“木”(線分)の配列である[1] 。厳密は、ユークリッドの果樹園は、正の整数 i と j に対する (i, j, 0) から (i, j, 1) までの線分の集合である


原点から(m, n, 0) の木が見えることは、m と n が互いに素であることと同値である。すなわち、m/n が既約分数であることに対応する。ユークリッドの果樹園という名は、互いに素であるかを判定する(最大公約数を求める)ユークリッドの互除法にちなむ。
果樹園の頂点を原点に対して平面 x + y = 1 に投影すると、トマエ関数のグラフの一部をなす。点 (m, n, 1) は
に投影される。
関連項目
[編集]参考文献
[編集]- ^ Weisstein, Eric W. "Euclid's Orchard". mathworld.wolfram.com (英語).
外部リンク
[編集]- Euclid's Orchard, Grade 9-11 activities and problem sheet, Texas Instruments Inc.
- Project Euler related problem

