共形同値
表示
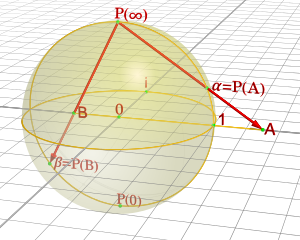
数学と理論物理学において、2つの幾何学が共形同値 (conformally equivalent) であるとは、一方の幾何学からもう一方の幾何学への共形変換(角度を保存する変換)が存在する場合をいう[1]。より一般的には、多様体 M 上の2つのリーマン計量が共形同値とは、M 上の正値関数を掛けることで一方から他方の計量が得られる場合をいう[2]。共形同値は、幾何学あるいはリーマン計量上の同値関係である。
関連項目
[編集]参考文献
[編集]- ^ Conway, John B. (1995), Functions of One Complex Variable II, Graduate Texts in Mathematics, 159, Springer, p. 29, ISBN 9780387944609.
- ^ Ramanan, S. (2005), Global Calculus, American Mathematical Society, p. 221, ISBN 9780821872406.

