円周角

円周角(えんしゅうかく)とは、ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことである。
円周角 θ (rad) は 0< θ <π を満たす。
円周角の定理
[編集]
円周角を作る三角形が円の中心を含む場合、円周角が長円弧上のどこにあっても、その大きさは変わらない。また、その円周角は、中心角の半分となる。これが円周角の定理である。
円周角を作る三角形が円の中心を含まない場合、円周角が短円弧上のどこにあっても、その大きさは変わらない。また、その円周角の補角は、中心角の半分となる。これも円周角の定理である。
円周角が長円弧上にある場合について証明する(右図)。長円弧の両端の点をA, B、円周角がある点をCとする。円の中心をMとする。点Mと点Cを通る直線と、線分ABの交点を、点Dとする。線分AMと線分ACは、共に円の半径なので、三角形AMCは二等辺三角形である。そのため角ACMと角CAMは等しい。さらに三角形の内角の和が180°であることと、角AMDが角AMCの補角であることから、角AMDは角ACDの2倍となる。同様に、角BMDは角BCDの2倍となる。そのため、角AMB(中心角)は角ACB(円周角)の2倍となる。
この関係は、点Cが円周上のどこにあっても成り立つので、同じABについての円周角は常に等しくなる。
歴史
[編集]バビロニア数学
[編集]紀元前20世紀から紀元前17世紀頃に行われていたバビロニア数学で、円周角が直角の場合についての円周角の定理が知られていた[1]。
タレスの定理
[編集]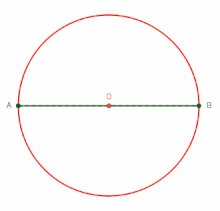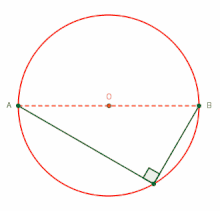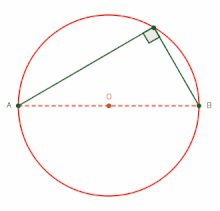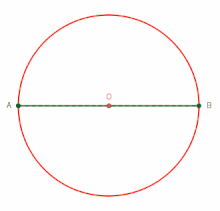
円周角が直角の場合についての円周角の定理は、上記の通りバビロニア人によって発見されたと思われるが、それは紀元前5世紀ごろには忘れられており、著名な数学者タレスやピタゴラスの発見だと思われていた[2][3]。
特に、紀元前7世紀から紀元前6世紀の人物タレスについては、3世紀の歴史家ディオゲネス・ラエルティオスが著書の中で「1世紀の歴史家エピダウロスのパンフィレの著作に『タレスは円の中に直角三角形を描いた最初の人物である』と書かれている」と言及したことが知られている[4]。
しかし現在では、ギリシアでこの手の理論が発達するのは紀元前4世紀以降であり、「タレスが発見した」というのは当時の推測に過ぎないと考えられている[2][5]。
ユークリッド原論
[編集]紀元前4世紀頃の著作と考えられているユークリッド原論の第3巻の命題20では、次のように述べられている[6]。
点ABCを通る円の中心をEとしたとき、角BECは角BACの2倍となる。
また、命題21では次のように述べられている。
円周上の点ABDEについて、角BADと角BEDは等しい。円の中心をFとする。まず線分BAEDが半円よりも大きくなる時、角BFDは角BADの2倍である。同様に角BFDは角BEDの2倍である。従って角BADは角BEDに等しい。次にBAEDが半円よりも小さい時、AFを通る線分と円の交点をCとする。四角形BAECは半円より大きいため角BACは角BECと等しい。同様に四角形CAEDは半円より大きいので、角CADと角CEDは等しい。従って角BADは角BEDに等しい。
また、命題31では次のように述べられている。
円周上の点ABCDについて、中心をEとする。線分BCで円を切ると半円となる場合、角BACは直角となり、角ABCは直角より小さくなり、角ADCは直角より大きくなければならない。線分EAはEBと等しいので、角EABは角EBAと等しい。また、線分EAはECと等しいので、角EACは角ECAと等しい。従って角BACは角ABCとACBの合計となる。一方三角形ABCの外角FACは、角ABCとACBの合計に等しい。従って角BACは角FACと等しい。従って、それぞれ直角である。従って、角BACは直角である。
アルハゼンの定理
[編集]
11世紀にイスラーム圏で活躍した数学者イブン・ハイサム(ラテン名アルハゼン)は、円の外にある点Eと、円周上にあり、三角形ABEが円の中心Qを含むような点A, Bについて、線分AEと円の交点をC、線分BEと円の交点をD、線分ADとBCの交点をPとした時、角AEB=角ADB-角CBDであることを発見した。
著名人による言及
[編集]
詩人ダンテが14世紀に書いた叙事詩『神曲』の天国編第13歌には、「もしも半円の中に直角を持たない三角形を描けるのであれば」という、タレスの定理を前提とした節がある[7][8]。
脚注
[編集]- ^ de Laet, Siegfried J. (1996). History of Humanity: Scientific and Cultural Development. UNESCO, Volume 3, p. 14. ISBN 92-3-102812-X
- ^ a b Dicks, D. R. (1959). “Thales”. The Classical Quarterly 9 (2): 294–309.
- ^ Allen, G. Donald (2000年). “Thales of Miletus”. 2012年2月12日閲覧。
- ^ Patronis, Tasos; Patsopoulos, Dimitris (January 2006). “The Theorem of Thales: A Study of the Naming of Theorems in School Geometry Textbooks”. The International Journal for the History of Mathematics Education: 57–68. ISSN 1932-8826. オリジナルの2018-04-25時点におけるアーカイブ。.
- ^ Sidoli, Nathan (2018). “Greek mathematics”. In Jones, A.; Taub, L.. The Cambridge History of Science: Vol. 1, Ancient Science. Cambridge University Press. pp. 345–373
- ^
 英語版ウィキソースに本記事に関連した原文があります:The_Elements_of_Euclid_for_the_Use_of_Schools_and_Colleges/Book_III PROPOSITION 20
英語版ウィキソースに本記事に関連した原文があります:The_Elements_of_Euclid_for_the_Use_of_Schools_and_Colleges/Book_III PROPOSITION 20
- ^ 藤谷道夫「ダンテ『神曲』の幾何学的構成について」『帝京大学外国語外国文学論集』第15巻、2009年2月15日、27-64頁、CRID 1050001337976609664、hdl:10682/832。
- ^
 英語版ウィキソースに本記事に関連した原文があります:Divine_Comedy_(Longfellow_1867)/Volume_3/Canto_13 ‘’Non si est dare primum motum ess’’
英語版ウィキソースに本記事に関連した原文があります:Divine_Comedy_(Longfellow_1867)/Volume_3/Canto_13 ‘’Non si est dare primum motum ess’’




