利用者‐会話:YUYA1996YUYA/sandbox

固有音響インピーダンスとは音波が伝わる空間における任意の点の音圧と粒子の変位速度との比である。量記号はZ_c、単位記号は Pa・s/m (=N・s/m³ )。 エネルギー損失がない無限に広がる媒質では固有音響インピーダンスはその媒質の密度ρとその媒質を伝わる音速cとの積に等しい。 音圧と粒子の変位速度の比で表される固有音響インピーダンスは、電圧と電流の比である電気回路の特性インピーダンスに対応している。

音響インピーダンス

音波が伝わる空間における平行で有限な面にはたらく音圧とその面Aを通過する体積速度との比である。量記号はZ_a、単位記号は Pa・s/m³ (= N・s/m⁵ )。 無限に長い管壁が剛体で、完全に滑らかで、かつ断熱的である円筒状パイプような管内を伝搬する波を考えたとき、音響インピーダンスは次のようになる。

$Z_{a}={\frac {\rho c}{A}}.$

固有音響インピーダンスの導出

図は、点Pにある粒子にx方向から音圧ｐがはたらいて、δt秒後にε_xだけ変位し、点Qにある粒子はε'_xだけ変位したことを示している。

密度ρの媒体で点Pと点Qを含む微小体積V(=δxδyδz)を考えたとき、点Pにある粒子にx方向の音圧ｐが働くと、δt秒後にε_xだけ変位し、点Qにある粒子はε' _xだけ変位する。

x は音波の伝搬方向に沿った空間の変数を指す。

運動方程式より

$\rho {\frac {\partial ^{2}{\varepsilon }_{x}}{\partial t^{2}}}=-{\frac {\partial p}{\partial x}}.$

圧力による微小体積の増分は、

$\delta V=V{\frac {\partial {\varepsilon }_{x}}{\partial x}}$　と計算できる。

上の式と体積弾性率の定義を用いると

$p=-K{\frac {\partial {\varepsilon }_{x}}{\partial x}}$　

となる。

これらより、以下の式が得られる。

${\frac {\partial ^{2}{\varepsilon }_{x}}{\partial t^{2}}}={\frac {K}{\rho }}{\frac {\partial ^{2}{\varepsilon }_{x}}{\partial x^{2}}}.$

この式は1次元波動方程式であるため、

$c={\sqrt {\frac {K}{\rho }}}$であることが分かる。

この波動方程式の解はxの正の方向に進む波と負に方向に進む波の和で構成される

${\varepsilon }_{x}(x,t)=f(x-ct)+g(x+ct)$

よって、

$u(x,t)={\frac {\partial {\varepsilon }_{x}}{\partial t}}=-c{\big [}f'(x-ct)-g'(x+ct){\big ]},$

$p(x,t)=-K{\frac {\partial {\varepsilon }_{x}}{\partial x}}=-\rho c^{2}{\big [}f'(x-ct)+g'(x+ct){\big ]}.$

進行波は、

${\begin{cases}p(x,t)=-\rho c^{2}\,f'(x-ct)\\u(x,t)=-c\,f'(x-ct)\end{cases}}$

もしくは、

${\begin{cases}p(x,t)=-\rho c^{2}\,g'(x+ct)\\u(x,t)=c\,g'(x+ct).\end{cases}}$

である。

この圧力波と粒子の変位速度の波の比の絶対値は、固有音響インピーダンスと呼ばれ Z_cと表される。

$Z_{c}=\rho c.$

媒体	密度ρ(kg/m3)	音速c(m/s)	固有音響インピーダンスZc(106kg/ m2s)
空気	1.3	330	0.00043
水	1000	1500	1.5
銅	7700	5850	45.0
ゴム	950	1500	1.5

反射と透過

図のような異なる媒体1と媒体2を考え、平面波の入射と反射と透過を示す。

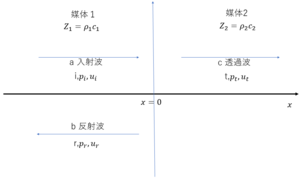x<0からx方向に波が進行していくとx=0で反射と透過が起こる。x<0では媒体1を通過する入射波と反射波を示していて、x>0では媒体2を通過する透過波を示している。

Z₁:媒質1の固有音響インピーダンス

Z₂:媒質2の固有音響インピーダンス

x=0における音圧の入射波をp_i、音圧の反射波をp_r、音圧の透過波をp_t、

粒子の変位速度の入射波をu_i、粒子の変位速度の反射波をu_r、粒子の変位速度の透過波をu_tと示す。

x=0では連続性より、以下の式が示される。

${p_{i}}+{p_{r}}={p_{t}}$

${u_{i}}+{u_{r}}={u_{t}}$

これらの式を用いると、

音圧の反射率　　　　　:$R_{p}={\frac {p_{r}}{p_{i}}}={\frac {Z_{2}-Z_{1}}{Z_{2}+Z_{1}}}$

音圧の透過率　　　　　:$T_{p}={\frac {p_{t}}{p_{i}}}={\frac {2Z_{2}}{Z_{2}+Z_{1}}}$

粒子の変位速度の反射率　　　:$R_{u}={\frac {u_{r}}{u_{i}}}=-{\frac {Z_{2}-Z_{1}}{Z_{2}+Z_{1}}}$

粒子の変位速度の透過率　　　:$T_{u}={\frac {u_{t}}{u_{i}}}={\frac {2Z_{1}}{Z_{2}+Z_{1}}}$

と計算できる。

単位時間に単位面積あたりに通過する音のエネルギーは$I=up$と表すことができる。 音のエネルギーの入射波をI_i、音のエネルギーの反射波をI_r、音のエネルギーの透過波をI_tと表すと、

音のエネルギーの反射率:$R_{I}={\frac {I_{r}}{I_{i}}}=|{\frac {Z_{2}-Z_{1}}{Z_{2}+Z_{1}}}|^{2}$

音のエネルギーの透過率:$T_{I}={\frac {I_{t}}{I_{i}}}=|{\frac {4Z_{1}Z_{2}}{(Z_{2}+Z_{1})^{2}}}|$

反射損失

音のエネルギーの反射率をデシベル値で表したものを反射損失という 反射損失をR_lossと表すと、

$R_{loss}=10\log _{10}{\frac {1}{R_{I}}}=10\log _{10}{\frac {I_{i}}{I_{r}}}.$

透過損失

音のエネルギーの透過率をデシベル値で表したものを透過損失という。 透過損失をT_lossと表すと、

$T_{loss}=10\log _{10}{\frac {1}{T_{I}}}=10\log _{10}{\frac {I_{i}}{I_{t}}}.$

透過損失は実用的には壁や床などの遮音性能を表す数値として用いられている。 遮音性能が大きいほど、透過する音が小さい。

関連項目

特性インピーダンス

音圧

音速

反射損失

透過損失

遮音性能

音響インピーダンス

参考文献

「楽器の物理学」　N・H・フレッチャー/T・D・ロッシング[著]岸憲史/久保田秀美/吉川茂[訳]　丸善出版

「新版　音響用語辞典」　日本音響学会　編　コロナ社

「新音響・音声工学」　古井貞煕　著　近代科学者

「音響バブルとそのケミストリー」　崔 博坤 、 原田 久志 、興津 健二、榎本　尚也　編著　コロナ社