利用者:加藤勝憲/ メカニカル・フィルター

メカニカル・フィルターは、通常、無線周波数において電子フィルターの代わりに使用される信号処理フィルターである。その目的は通常の電子フィルターと同じで、ある範囲の信号周波数を通過させ、それ以外の周波数を遮断することである。このフィルターは、電気信号のアナログである機械的振動に作用する。フィルターの入力と出力では、トランスデューサーが電気信号を機械的振動に変換し、また機械的振動から電気信号に戻している。

機械式フィルターの構成要素はすべて、電気回路に見られるさまざまな要素に直接類似している。機械的要素は、対応する電気的要素と同一の数学的関数に従う。このため、電気回路網の解析やフィルター設計の手法を機械式フィルターに適用することが可能である。電気理論は、有用なフィルター周波数応答を生成する数学形式の大規模なライブラリを開発し、機械フィルター設計者はこれらを直接利用することができる。機械部品を適切な値に設定するだけで、電気的なものと同一の応答を持つフィルターができあがる。frequency responses

鋼鉄合金と鉄・ニッケル合金は、機械式フィルター部品の一般的な材料であり、ニッケルは入出力カップリングに使われることもある。これらの材料で作られたフィルターの共振器は、最終組立前に共振周波数を精密に調整するために機械加工する必要がある。

この記事で言うメカニカル・フィルターとは、電気機械的な役割で使われるものであるが、機械的な振動や音波（これも本質的には機械的なものである）を直接フィルターするために、機械的な設計を使うことも可能である。例えば、ラウドスピーカー・キャビネットの設計におけるオーディオ周波数特性のフィルタリングは、機械部品で実現できる。電気的な用途では、電気的な対応物に対応する機械的な部品に加えて、機械的な領域と電気的な領域を変換するための変換器が必要となる。本稿では、機械的フィルターのための多種多様な部品形態とトポロジーの代表的なものを紹介する。

While the meaning of mechanical filter in this article is one that is used in an electromechanical role, it is possible to use a mechanical design to filter mechanical vibrations or sound waves (which are also essentially mechanical) directly. For example, filtering of audio frequency response in the design of loudspeaker cabinets can be achieved with mechanical components. In the electrical application, in addition to mechanical components which correspond to their electrical counterparts, transducers are needed to convert between the mechanical and electrical domains. A representative selection of the wide variety of component forms and topologies for mechanical filters are presented in this article.

機械式フィルターの理論は、1920年代に蓄音機の機械部品の改良に初めて応用された。1950年代には、機械式フィルターはラジオ送信機や高級受信機用の独立した部品として製造されるようになっていた。機械共振器が達成できる「品質係数」Qは、電気回路のみのLC回路よりもはるかに高く、優れた選択性を持つ機械式フィルターの製造を可能にした。ラジオ受信機にとって選択性が良好であることは重要であり、このようなフィルターは非常に魅力的であった。現代の研究者たちは、電子集積回路に対応する機械装置であるマイクロエレクトロメカニカルフィルターの研究に取り組んでいる。

The theory of mechanical filters was first applied to improving the mechanical parts of phonographs in the 1920s. By the 1950s mechanical filters were being manufactured as self-contained components for applications in radio transmitters and high-end receivers. The high "quality factor", Q, that mechanical resonators can attain, far higher than that of an all-electrical LC circuit, made possible the construction of mechanical filters with excellent selectivity. Good selectivity, being important in radio receivers, made such filters highly attractive. Contemporary researchers are working on microelectromechanical filters, the mechanical devices corresponding to electronic integrated circuits.

Elements

受動線形電気ネットワークの要素は、それぞれインダクタンス、エラストンス(逆静電容量)、抵抗の特性を持つインダクタ、コンデンサ、抵抗で構成される。これらの特性の機械的な対応物は、それぞれ質量、剛性、減衰である。ほとんどの電子フィルタ設計では、フィルタ本体にはインダクタとコンデンサの要素のみが使用される(ただし、フィルタは入力と出力で抵抗で終端される場合がある)。抵抗は理想的なコンポーネントで構成される理論上のフィルターには存在せず、実際的な設計においてのみ、望ましくない寄生要素として発生する。同様に、機械的なフィルターは理想的には質量と剛性の特性を持つコンポーネントのみで構成されるが、実際にはある程度の減衰も存在する。[1]

The elements of a passive linear electrical network consist of inductors, capacitors and resistors which have the properties of inductance, elastance (inverse capacitance) and resistance, respectively. The mechanical counterparts of these properties are, respectively, mass, stiffness and damping. In most electronic filter designs, only inductor and capacitor elements are used in the body of the filter (although the filter may be terminated with resistors at the input and output). Resistances are not present in a theoretical filter composed of ideal components and only arise in practical designs as unwanted parasitic elements. Likewise, a mechanical filter would ideally consist only of components with the properties of mass and stiffness, but in reality some damping is present as well.^[1]

このタイプの分析における電圧と電流の機械的な対応物は、それぞれ力(F)と速度(v)であり、信号波形を表す。これより、機械インピーダンスは虚数角周波数jωで定義することができ、これは完全に電気的な類推に従うものである。[2][3]

The mechanical counterparts of voltage and electric current in this type of analysis are, respectively, force (F) and velocity (v) and represent the signal waveforms. From this, a mechanical impedance can be defined in terms of the imaginary angular frequency, jω, which entirely follows the electrical analogy.^[2]^[3]

表に示されたこの方式は、インピーダンスアナロジーとして知られている。このアナロジーを用いて作成された回路図は、電気回路から見た機械システムの電気インピーダンスと一致し、電気工学の観点から直感的に理解できる。また、力は電流に、速度は電圧に対応するモビリティアナロジー(注釈1)もある。この方式でも同様に有効な結果が得られるが、上記の電気的対応物の逆数を使用する必要がある。したがって、M → C , S → 1/L ,S → 1/L , D → G ここで G は電気コンダクタンス(リアクタンスが存在しない場合の抵抗の逆数)である。この方式で作成された等価回路は類似しているが、直列素子が並列になり、コンデンサがインダクタになるなど、インピーダンスの二重形式である。[4] 移動度のアナロジーを用いた回路図は、回路の機械的な配置により密接に一致し、機械工学の観点からはより直感的である。[5] 電気機械システムへの応用に加え、これらのアナロジーは音響学の分析を支援するために広く使用されている。[6]

The scheme presented in the table is known as the impedance analogy. Circuit diagrams produced using this analogy match the electrical impedance of the mechanical system seen by the electrical circuit, making it intuitive from an electrical engineering standpoint. There is also the mobility analogy,^{[注釈 1]} in which force corresponds to current and velocity corresponds to voltage. This has equally valid results but requires using the reciprocals of the electrical counterparts listed above. Hence, $M$ → $C$ , $S$ → 1/ $L$ , $S$ → 1/ $L$ , $D$ → $G$ where $G$ is electrical conductance (the reciprocal of resistance, if there is no reactance). Equivalent circuits produced by this scheme are similar, but are the dual impedance forms whereby series elements become parallel, capacitors become inductors, and so on.^[6] Circuit diagrams using the mobility analogy more closely match the mechanical arrangement of the circuit, making it more intuitive from a mechanical engineering standpoint.^[7] In addition to their application to electromechanical systems, these analogies are widely used to aid analysis in acoustics.^[8]

機械部品には、質量と剛性の両方が不可避的に備わっている。これを電気的な用語に置き換えると、LC回路、つまりインダクタとコンデンサで構成される回路となる。したがって、機械部品は共振器であり、そのように使用されることが多い。望ましくない特性を最小化(完全に排除することはできない)することで、機械的な実装においてインダクタとコンデンサを個別の集中定数素子として表現することは依然として可能である。コンデンサは、細長い棒状に作られ、質量は最小限に抑えられ、コンプライアンスは最大限に高められる。一方、インダクタは、短い幅広の部品で作られ、コンプライアンスに比べ質量が最大限に高められる^[9]。

機械部品は機械的振動の伝送路として作用する。部品に比べて波長が短い場合、上述の集中定数モデルはもはや適切ではなく、分布定数モデルを使用しなければならない。機械的分布定数は電気的分布定数と完全に類似しており、機械的フィルター設計者は電気的分布定数フィルター設計の手法を使用することができる。[7]

Mechanical parts act as a transmission line for mechanical vibrations. If the wavelength is short in comparison to the part then a lumped-element model as described above is no longer adequate and a distributed-element model must be used instead. The mechanical distributed elements are entirely analogous to electrical distributed elements and the mechanical filter designer can use the methods of electrical distributed-element filter design.^[9]

History

Harmonic telegraph

電気フィルター理論で発見されたことを力学に応用することで、機械式フィルターの設計が開発された。しかし、音響フィルターの初期の例(1870年代)としては、「調和電信」が挙げられる。調和電信は、電気共鳴が十分に理解されていなかった一方で、機械共鳴(特に音響共鳴)は技術者にとって非常に馴染み深いものであったため、まさにそのような状況下で生まれたものである。しかし、この状況は長くは続かなかった。電気共鳴はそれより前から科学的に知られており、エンジニアたちがフィルターの完全な電気設計を始めるのにそれほど時間はかからなかった。しかし、調和電信は当時としてはある程度の重要性を持っていた。そのアイデアは、現在では周波数分割多重化と呼ばれる方法で、1本の電信線上で複数の電信信号を組み合わせるというもので、これにより電信線の設置コストを大幅に削減することができた。各オペレーターの電鍵が振動する電気機械式リードを起動し、この振動を電気信号に変換した。受信オペレーターでのフィルタリングは、全く同じ周波数に調整された同様のリードによって実現され、同じチューニングのオペレーターからの送信のみが振動し、音を発生させる^[10]^[11]。

"harmonic telegraph", which arose precisely because electrical resonance was poorly understood but mechanical resonance (in particular, acoustic resonance) was very familiar to engineers. This situation was not to last for long; electrical resonance

イライシャ・グレイ、アレクサンダー・グラハム・ベル、アーネスト・メルカディエ[注釈 1] などによって、調和電信の改良版が開発された。電気領域における音響変換器として機能する能力が、電話の発明のきっかけとなった^[10]^[11]。

Ernest Mercadier^{[注釈 2]} and others. Its ability to act as a sound transducer

Mechanical equivalent circuits

電気ネットワーク解析の基本が確立されると、複雑インピーダンスとフィルター設計理論の概念が類推によって力学に持ち込まれるのにそれほど時間はかからなかった。また、複素インピーダンスの導入にも携わったケネリーとウェブスターは、1920年にインピーダンスの概念を機械システムに初めて拡張した。[10] 機械アドミタンスと関連するモビリティの類推は、それよりずっと後の1932年のファイストンの功績である。[11][12]

Once the basics of electrical network analysis began to be established, it was not long before the ideas of complex impedance and filter design theories were carried over into mechanics by analogy. Kennelly, who was also responsible for introducing complex impedance, and Webster were the first to extend the concept of impedance into mechanical systems in 1920.^[12] Mechanical admittance and the associated mobility analogy came much later and are due to Firestone in 1932.^[13]^[14]

単に機械的な類似性を開発するだけでは不十分であった。これは完全に機械的な領域の問題に適用できるが、電気的な応用を持つ機械的なフィルタの場合は、類似性の中にトランスデューサも含める必要がある。ポアンカレ(1907年)^[15]は、電気変数(電圧および電流)と機械変数(力および速度)を関連付ける線形代数方程式のペアとしてトランスデューサを初めて説明した^[15]。これらの方程式は、電気理論における2ポートネットワークのZパラメータとほぼ同様に、行列関係式として表現することができる。これは完全に類似している。

linear algebraic、z-parameters of a two-port network in electrical theory, to which this is entirely analogous:

{\begin{bmatrix}V\\F\end{bmatrix}}={\begin{bmatrix}z_{11}&z_{12}\\z_{21}&z_{22}\end{bmatrix}}{\begin{bmatrix}I\\v\end{bmatrix}}

ここで、V と I はそれぞれトランスデューサの電気側における電圧と電流を表す。

1921年、Wegelは、これらの方程式を機械インピーダンスおよび電気インピーダンスの観点から初めて表現した。素子は開回路機械インピーダンスであり、すなわち、電気側へ電流が流れていない場合のトランスデューサの機械側が示すインピーダンスである。素子は逆にクランプされた電気インピーダンスであり、すなわち、機械側がクランプされ、移動が阻止されている場合(速度はゼロ)の電気側が示すインピーダンスである。残りの2つの要素は、それぞれトランスデューサの順方向および逆方向伝達関数を表す。これらの考え方が確立されると、エンジニアは電気理論を機械分野に拡張し、電気機械システムを統一された全体として分析することが可能になった^[12]^[16]。

Sound reproduction

これらの新しい理論的ツールの初期の応用例は、蓄音機の音の再生であった。初期の蓄音機の設計で繰り返し発生した問題は、ピックアップと音の伝達メカニズムにおける機械的共振が周波数応答に過度に大きなピークと谷を生じさせ、音質を低下させていたことである。1923年、ウェスタン・エレクトリック社のハリソンは、機械設計が電気回路として完全に表現された蓄音機の特許を出願した。蓄音機のホーンは伝送線路として表され、回路の残りの部分に対して抵抗負荷となる。一方、機械および音響部品(ピックアップの針からホーンまで)は、インピーダンスの類推に従って集中定数素子に変換される。最終的に到達した回路は、並列共振回路を並列コンデンサで結合した梯子型トポロジーである。これはバンドパスフィルタ回路と見なすことができる。ハリソンは、このフィルタのコンポーネント値を設計し、希望するオーディオ通過帯域(この場合は100Hzから6kHz)に対応する特定の通過帯域とフラットなレスポンスを実現した。これらの電気的要素値を機械的量に変換することで、質量と剛性という観点から機械的コンポーネントの仕様が得られ、さらに製造のための物理的寸法に変換することができた。その結果、レコードプレーヤーは通過帯域においてフラットな周波数特性を持ち、以前に経験した共振が解消された^[17]。その後まもなく、ハリソンは同じ手法を電話機の送話器と受話器に応用した別の特許を出願した^[18]。

Harrison used Campbell's image filter theory, which was the most advanced filter theory available at the time. In this theory, filter design is viewed essentially as an impedance matching problem.^[19] More advanced filter theory was brought to bear on this problem by Norton in 1929 at Bell Labs. Norton followed the same general approach though he later described to Darlington the filter he designed as being "maximally flat".^[1] Norton's mechanical design predates the paper by Butterworth who is usually credited as the first to describe the electronic maximally flat filter.^[20] The equations Norton gives for his filter correspond to a singly terminated Butterworth filter, that is, one driven by an ideal voltage source with no impedance, whereas the form more usually given in texts is for the doubly terminated filter with resistors at both ends, making it hard to recognise the design for what it is.^[21] Another unusual feature of Norton's filter design arises from the series capacitor, which represents the stiffness of the diaphragm. This is the only series capacitor in Norton's representation, and without it, the filter could be analysed as a low-pass prototype. Norton moves the capacitor out of the body of the filter to the input at the expense of introducing a transformer into the equivalent circuit (Norton's figure 4). Norton has used here the "turning round the L" impedance transform to achieve this.^[22]

The definitive description of the subject from this period is Maxfield and Harrison's 1926 paper. There, they describe not only how mechanical bandpass filters can be applied to sound reproduction systems, but also apply the same principles to recording systems and describe a much improved disc cutting head.^[23]^[24]

Volume production

Modern mechanical filters for intermediate frequency (IF) applications were first investigated by Robert Adler of Zenith Electronics who built a 455 kHz filter in 1946.^[25] The idea was taken up by Collins Radio Company who started the first volume production of mechanical filters from the 1950s onwards. These were originally designed for telephone frequency-division multiplex applications where there is commercial advantage in using high quality filters. Precision and steepness of the transition band leads to a reduced width of guard band, which in turn leads to the ability to squeeze more telephone channels into the same cable. This same feature is useful in radio transmitters for much the same reason. Mechanical filters quickly also found popularity in VHF/UHF radio IF stages of the high end radio sets (military, marine, amateur radio and the like) manufactured by Collins. They were favoured in the radio application because they could achieve much higher $Q$ -factors than the equivalent LC filter. High $Q$ allows filters to be designed which have high selectivity, important for distinguishing adjacent radio channels in receivers. They also had an advantage in stability over both LC filters and monolithic crystal filters. The most popular design for radio applications was torsional resonators because radio IF typically lies in the 100 to 500 kHz band.^[26]^[27]

Transducers

Both magnetostrictive and piezoelectric transducers are used in mechanical filters. Piezoelectric transducers are favoured in recent designs since the piezoelectric material can also be used as one of the resonators of the filter, thus reducing the number of components and thereby saving space. They also avoid the susceptibility to extraneous magnetic fields of the magnetostrictive type of transducer.^[28]

Magnetostrictive

A magnetostrictive material is one which changes shape when a magnetic field is applied. In reverse, it produces a magnetic field when distorted. The magnetostrictive transducer requires a coil of conducting wire around the magnetostrictive material. The coil either induces a magnetic field in the transducer and sets it in motion or else picks up an induced current from the motion of the transducer at the filter output. It is also usually necessary to have a small magnet to bias the magnetostrictive material into its operating range. It is possible to dispense with the magnets if the biasing is taken care of on the electronic side by providing a d.c. current superimposed on the signal, but this approach would detract from the generality of the filter design.^[29]

The usual magnetostrictive materials used for the transducer are either ferrite or compressed powdered iron. Mechanical filter designs often have the resonators coupled with steel or nickel-iron wires, but on some designs, especially older ones, nickel wire may be used for the input and output rods. This is because it is possible to wind the transducer coil directly on to a nickel coupling wire since nickel is slightly magnetostrictive. However, it is not strongly so and coupling to the electrical circuit is weak. This scheme also has the disadvantage of eddy currents, a problem that is avoided if ferrites are used instead of nickel.^[29]

The coil of the transducer adds some inductance on the electrical side of the filter. It is common practice to add a capacitor in parallel with the coil so that an additional resonator is formed which can be incorporated into the filter design. While this will not improve performance to the extent that an additional mechanical resonator would, there is some benefit and the coil has to be there in any case.^[30]

Piezoelectric

A piezoelectric material is one which changes shape when an electric field is applied. In reverse, it produces an electric field when it is distorted. A piezoelectric transducer, in essence, is made simply by plating electrodes on to the piezoelectric material. Early piezoelectric materials used in transducers such as barium titanate had poor temperature stability. This precluded the transducer from functioning as one of the resonators; it had to be a separate component. This problem was solved with the introduction of lead zirconate titanate (abbreviated PZT) which is stable enough to be used as a resonator. Another common piezoelectric material is quartz, which has also been used in mechanical filters. However, ceramic materials such as PZT are preferred for their greater electromechanical coupling coefficient.^[31]

One type of piezoelectric transducer is the Langevin type, named after a transducer used by Paul Langevin in early sonar research. This is good for longitudinal modes of vibration. It can also be used on resonators with other modes of vibration if the motion can be mechanically converted into a longitudinal motion. The transducer consists of a layer of piezoelectric material sandwiched transversally into a coupling rod or resonator.^[32]

Another kind of piezoelectric transducer has the piezoelectric material sandwiched in longitudinally, usually into the resonator itself. This kind is good for torsional vibration modes and is called a torsional transducer.^[33]

As miniaturized by using thin film manufacturing methods piezoelectric resonators are called thin-film bulk acoustic resonators (FBARs).

Resonators

Material	$Q$ -factor
Nickel	several 100^[34]
Steel	several 1000^[34]
Aluminium	~10,000^[34]
Nickel-iron alloy	10,000 to 25,000^[35] depending on composition

It is possible to achieve an extremely high $Q$ with mechanical resonators. Mechanical resonators typically have a $Q$ of 10,000 or so, and 25,000 can be achieved in torsional resonators using a particular nickel-iron alloy. This is an unreasonably high figure to achieve with LC circuits, whose $Q$ is limited by the resistance of the inductor coils.^[29]^[35]^[36]

Early designs in the 1940s and 1950s started by using steel as a resonator material. This has given way to nickel-iron alloys, primarily to maximise the $Q$ since this is often the primary appeal of mechanical filters rather than price. Some of the metals that have been used for mechanical filter resonators and their $Q$ are shown in the table.^[35]

Piezoelectric crystals are also sometimes used in mechanical filter designs. This is especially true for resonators that are also acting as transducers for inputs and outputs.^[35]

One advantage that mechanical filters have over LC electrical filters is that they can be made very stable. The resonance frequency can be made so stable that it varies only 1.5 parts per billion (ppb) from the specified value over the operating temperature range (−25 to 85 °C), and its average drift with time can be as low as 4 ppb per day.^[37] This stability with temperature is another reason for using nickel-iron as the resonator material. Variations with temperature in the resonance frequency (and other features of the frequency function) are directly related to variations in the Young's modulus, which is a measure of stiffness of the material. Materials are therefore sought that have a small temperature coefficient of Young's modulus. In general, Young's modulus has a negative temperature coefficient (materials become less stiff with increasing temperature) but additions of small amounts of certain other elements in the alloy^{[注釈 3]} can produce a material with a temperature coefficient that changes sign from negative through zero to positive with temperature. Such a material will have a zero coefficient of temperature with resonance frequency around a particular temperature. It is possible to adjust the point of zero temperature coefficient to a desired position by heat treatment of the alloy.^[36]^[39]

Resonator modes

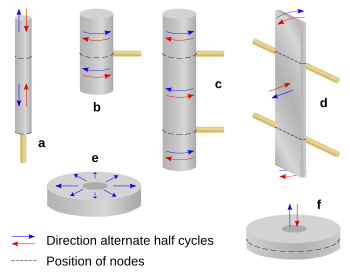
It is usually possible for a mechanical part to vibrate in a number of different modes, however the design will be based on a particular vibrational mode and the designer will take steps to try to restrict the resonance to this mode. As well as the straightforward longitudinal mode some others which are used include flexural mode, torsional mode, radial mode and drumhead mode.^[40]^[41]

Modes are numbered according to the number of half-wavelengths in the vibration. Some modes exhibit vibrations in more than one direction (such as drumhead mode which has two) and consequently the mode number consists of more than one number. When the vibration is in one of the higher modes, there will be multiple nodes on the resonator where there is no motion. For some types of resonator, this can provide a convenient place to make a mechanical attachment for structural support. Wires attached at nodes will have no effect on the vibration of the resonator or the overall filter response. In figure 5, some possible anchor points are shown as wires attached at the nodes.

Circuit designs

^ ^a ^b Darlington (1984)
^ Norton (1931)
^ Talbot-Smith (2001)
^ Gatti & Ferrari (1999), pp. 630–632
^ Johnson (1968), p. 41
^ Taylor & Huang (1997)
^ Eargle (2003)
^ Talbot-Smith (2001) for instance.
^ ^a ^b Norton (1931)
^ ^a ^b Lundheim (2002)
^ ^a ^b Blanchard (1944)
^ ^a ^b Hunt (1954)
^ Hunt (1954)
^ Pierce (1989) cites:

Firestone, F.A. (1932–1933). “A new analogy between mechanical and electrical systems”. Journal of the Acoustical Society of America 4 (3): 249–267. doi:10.1121/1.1915605.
^ ^a ^b Pierce (1989) cites:

Poincaré, H. (1907). “Etude du récepteur téléphonique”. Eclairage Electrique 50: 221–372.
^ Pierce (1989) cites:

Wegel, R.L. (1921). “Theory of magneto-mechanical systems as applied to telephone receivers and similar structures”. Journal of the American Institute of Electrical Engineers 40 (10): 791–802. doi:10.1109/JoAIEE.1921.6594447. https://zenodo.org/record/2476633.
^ Harrison (1929)
^ Harrison (1930)
^ Harrison (1929)
^ Butterworth, S. (1930). “On the theory of filter amplifiers”. Wireless Engineer 7: 536–541.
^ cf. Norton (1931) with Matthaei, pp.104–107.
^ Norton (1931)
^ Taylor & Huang (1997)
^ Hunt (1954) cites:

Maxfield, J.P.; Harrison, H.C. (1926). “Methods of high quality recording and reproducing of music and speech based on telephone research”. Bell System Technical Journal 5 (3): 493–523. doi:10.1002/j.1538-7305.1926.tb00118.x.
^ Drentea (2010)
^ Taylor & Huang (1997)
^ Carr (2002)
^ Taylor & Huang (1997)
^ ^a ^b ^c Carr (2002)
^ Mason (1961)
^ Rosen, Hiremath & Newnham (1992)
^ Rosen, Hiremath & Newnham (1992)
^ Rosen, Hiremath & Newnham (1992)
^ ^a ^b ^c George (1956)
^ ^a ^b ^c ^d Lin, Howe & Pisano (1998)
^ ^a ^b ^c Taylor & Huang (1997)
^ Carr (2002)
^ Gould (1960), p. 201
^ Schneider, Wolfgang; Thomas, Hans (1979). “Constant modulus alloys for mechanical oscillators”. Metallurgical Transactions 10 (4): 433. Bibcode: 1979MTA....10..433S. doi:10.1007/BF02697070.
^ “How mechanical filters work”. rockwellcollins.com. Rockwell-Collins. 11 November 2009閲覧。
^ Taylor & Huang (1997)

There are a great many combinations of resonators and transducers that can be used to construct a mechanical filter. A selection of some of these is shown in the diagrams. Figure 6 shows a filter using disc flexural resonators and magnetostrictive transducers. The transducer drives the centre of the first resonator, causing it to vibrate. The edges of the disc move in antiphase to the centre when the driving signal is at, or close to, resonance, and the signal is transmitted through the connecting rods to the next resonator. When the driving signal is not close to resonance, there is little movement at the edges, and the filter rejects (does not pass) the signal.^[1] Figure 7 shows a similar idea involving longitudinal resonators connected together in a chain by connecting rods. In this diagram, the filter is driven by piezoelectric transducers. It could equally well have used magnetostrictive transducers.^[2] Figure 8 shows a filter using torsional resonators. In this diagram, the input has a torsional piezoelectric transducer and the output has a magnetostrictive transducer. This would be quite unusual in a real design, as both input and output usually have the same type of transducer. The magnetostrictive transducer is only shown here to demonstrate how longitudinal vibrations may be converted to torsional vibrations and vice versa.^[2]^[3]^[4] Figure 9 shows a filter using drumhead mode resonators. The edges of the discs are fixed to the casing of the filter (not shown in the diagram) so the vibration of the disc is in the same modes as the membrane of a drum. Collins calls this type of filter a disc wire filter.^[3]

The various types of resonator are all particularly suited to different frequency bands. Overall, mechanical filters with lumped elements of all kinds can cover frequencies from about 5 to 700 kHz although mechanical filters down as low as a few kilohertz (kHz) are rare.^[5] The lower part of this range, below 100 kHz, is best covered with bar flexural resonators. The upper part is better done with torsional resonators.^[3] Drumhead disc resonators are in the middle, covering the range from around 100 to 300 kHz.^[1]

The frequency response behaviour of all mechanical filters can be expressed as an equivalent electrical circuit using the impedance analogy described above. An example of this is shown in figure 8b which is the equivalent circuit of the mechanical filter of figure 8a. Elements on the electrical side, such as the inductance of the magnetostrictive transducer, are omitted but would be taken into account in a complete design. The series resonant circuits on the circuit diagram represent the torsional resonators, and the shunt capacitors represent the coupling wires. The component values of the electrical equivalent circuit can be adjusted, more or less at will, by modifying the dimensions of the mechanical components. In this way, all the theoretical tools of electrical analysis and filter design can be brought to bear on the mechanical design. Any filter realisable in electrical theory can, in principle, also be realised as a mechanical filter. In particular, the popular finite element approximations to an ideal filter response of the Butterworth and Chebyshev filters can both readily be realised. As with the electrical counterpart, the more elements that are used, the closer the approximation approaches the ideal, however, for practical reasons the number of resonators does not normally exceed eight.^[1]^[6]

Semi-lumped designs

Frequencies of the order of megahertz (MHz) are above the usual range for mechanical filters. The components start to become very small, or alternatively the components are large compared to the signal wavelength. The lumped-element model described above starts to break down and the components must be considered as distributed elements. The frequency at which the transition from lumped to distributed modeling takes place is much lower for mechanical filters than it is for their electrical counterparts. This is because mechanical vibrations travel at the speed of sound for the material the component is composed of. For solid components, this is many times (x15 for nickel-iron) the speed of sound in air (343 m/s) but still considerably less than the speed of electromagnetic waves (approx. 3.00×10⁸ m/s in vacuum). Consequently, mechanical wavelengths are much shorter than electrical wavelengths for the same frequency. Advantage can be taken of these effects by deliberately designing components to be distributed elements, and the components and methods used in electrical distributed-element filters can be brought to bear. The equivalents of stubs and impedance transformers are both achievable. Designs which use a mixture of lumped and distributed elements are referred to as semi-lumped.^[7]

An example of such a design is shown in figure 10a. The resonators are disc flexural resonators similar to those shown in figure 6, except that these are energised from an edge, leading to vibration in the fundamental flexural mode with a node in the centre, whereas the figure 6 design is energised in the centre leading to vibration in the second flexural mode at resonance. The resonators are mechanically attached to the housing by pivots at right angles to the coupling wires. The pivots are to ensure free turning of the resonator and minimise losses. The resonators are treated as lumped elements; however, the coupling wires are made exactly one half-wavelength ( $λ / 2$ ) long and are equivalent to a $λ / 2$ open circuit stub in the electrical equivalent circuit. For a narrow-band filter, a stub of this sort has the approximate equivalent circuit of a parallel shunt tuned circuit as shown in figure 10b. Consequently, the connecting wires are being used in this design to add additional resonators into the circuit and will have a better response than one with just the lumped resonators and short couplings.^[7] For even higher frequencies, microelectromechanical methods can be used as described below.

Bridging wires

Bridging wires are rods that couple together resonators that are not adjacent. They can be used to produce poles of attenuation in the stopband. This has the benefit of increasing the stopband rejection. When the pole is placed near the passband edge, it also has the benefit of increasing roll-off and narrowing the transition band. The typical effects of some of these on filter frequency response are shown in figure 11. Bridging across a single resonator (figure 11b) can produce a pole of attenuation in the high stopband. Bridging across two resonators (figure 11c) can produce a pole of attenuation in both the high and the low stopband. Using multiple bridges (figure 11d) will result in multiple poles of attenuation. In this way, the attenuation of the stopbands can be deepened over a broad frequency range.^[8]

The method of coupling between non-adjacent resonators is not limited to mechanical filters. It can be applied to other filter formats and the general term for this class is cross-coupled filter. For instance, channels can be cut between cavity resonators, mutual inductance can be used with discrete component filters, and feedback paths can be used with active analogue or digital filters. Nor was the method first discovered in the field of mechanical filters; the earliest description is in a 1948 patent for filters using microwave cavity resonators.^[9] However, mechanical filter designers were the first (1960s) to develop practical filters of this kind and the method became a particular feature of mechanical filters.

Microelectromechanical filters

A new technology emerging in mechanical filtering is microelectromechanical systems (MEMS). MEMS are very small micromachines with component sizes measured in micrometres (μm), but not as small as nanomachines. These filters can be designed to operate at much higher frequencies than can be achieved with traditional mechanical filters. These systems are mostly fabricated from silicon (Si), silicon nitride (Si₃N₄), or polymers. A common component used for radio frequency filtering (and MEMS applications generally), is the cantilever resonator. Cantilevers are simple mechanical components to manufacture by much the same methods used by the semiconductor industry; masking, photolithography and etching, with a final undercutting etch to separate the cantilever from the substrate. The technology has great promise since cantilevers can be produced in large numbers on a single substrate—much as large numbers of transistors are currently contained on a single silicon chip.^[10]

The resonator shown in figure 12 is around 120 μm in length. Experimental complete filters with an operating frequency of 30 GHz have been produced using cantilever varactors as the resonator elements. The size of this filter is around 4×3.5 mm.^[11] Cantilever resonators are typically applied at frequencies below 200 MHz, but other structures, such as micro-machined cavities, can be used in the microwave bands.^[12] Extremely high $Q$ resonators can be made with this technology; flexural mode resonators with a $Q$ in excess of 80,000 at 8 MHz are reported.^[13]

Adjustment

The precision applications in which mechanical filters are used require that the resonators are accurately adjusted to the specified resonance frequency. This is known as trimming and usually involves a mechanical machining process. In most filter designs, this can be difficult to do once the resonators have been assembled into the complete filter so the resonators are trimmed before assembly. Trimming is done in at least two stages; coarse and fine, with each stage bringing the resonance frequency closer to the specified value. Most trimming methods involve removing material from the resonator which will increase the resonance frequency. The target frequency for a coarse trimming stage consequently needs to be set below the final frequency since the tolerances of the process could otherwise result in a frequency higher than the following fine trimming stage could adjust for.^[14]^[15]

The coarsest method of trimming is grinding of the main resonating surface of the resonator; this process has an accuracy of around ±800 ppm. Better control can be achieved by grinding the edge of the resonator instead of the main surface. This has a less dramatic effect and consequently better accuracy. Processes that can be used for fine trimming, in order of increasing accuracy, are sandblasting, drilling, and laser ablation. Laser trimming is capable of achieving an accuracy of ±40 ppm.^[15]^[16]

Trimming by hand, rather than machine, was used on some early production components but would now normally only be encountered during product development. Methods available include sanding and filing. It is also possible to add material to the resonator by hand, thus reducing the resonance frequency. One such method is to add solder, but this is not suitable for production use since the solder will tend to reduce the high $Q$ of the resonator.^[14]

In the case of MEMS filters, it is not possible to trim the resonators outside of the filter because of the integrated nature of the device construction. However, trimming is still a requirement in many MEMS applications. Laser ablation can be used for this but material deposition methods are available as well as material removal. These methods include laser or ion-beam induced deposition.^[17]

Footnotes

.mw-parser-output .reflist{margin-bottom:0.5em;list-style-type:decimal}@media screen{.mw-parser-output .reflist{font-size:90%}}.mw-parser-output .reflist .references{font-size:100%;margin-bottom:0;list-style-type:inherit}.mw-parser-output .reflist-columns-2{column-width:30em}.mw-parser-output .reflist-columns-3{column-width:25em}.mw-parser-output .reflist-columns{margin-top:0.3em}.mw-parser-output .reflist-columns ol{margin-top:0}.mw-parser-output .reflist-columns li{page-break-inside:avoid;break-inside:avoid-column}.mw-parser-output .reflist-upper-alpha{list-style-type:upper-alpha}.mw-parser-output .reflist-upper-roman{list-style-type:upper-roman}.mw-parser-output .reflist-lower-alpha{list-style-type:lower-alpha}.mw-parser-output .reflist-lower-greek{list-style-type:lower-greek}.mw-parser-output .reflist-lower-roman{list-style-type:lower-roman}