利用者:紅い目の女の子/力の平行四辺形

力の平行四辺形は物体に作用する2つの力の合力を求める(可視化する)ための手法。

図1:ベクトルの和を求めるための平行四辺形の作図

力はベクトルであるから、力の合成はベクトルの和の法則に従う。そのため、複数の力の合力を求めるには、合成する前のそれぞれの力をベクトルの意味の矢印で描けばよいということになる。

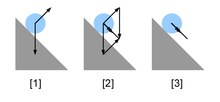
図1を例に、具体的に説明する。この図は、F{sub}1{/sub}とF{sub}2{/sub}を合成することによって合力F{sub}net{/sub}を求める方法を示している。図のようにF{sub}1{/sub}とF{sub}2{/sub}を一辺とする平行四辺形を作図すると、その対角線が合力F{sub}net{/sub}を表すベクトルになる。こうした作図は、F{sub}1{/sub}の終点とF{sub}2{/sub}の始点を接続することで、F{sub}1{/sub}の始点とF{sub}2{/sub}の終点を結ぶベクトルが2つのベクトルの和になることに対応している。3つ目の力F{sub}3{/sub}がある場合には、F{sub}1{/sub}+F{sub}2{/sub}とF{sub}3{/sub}に同様の操作を行うことで、3力の合力を求めることができる。従って、3つ以上の力が作用する時にも、作図される図形はもはや平行四辺形ではないけれども、全く同じ原理に基づいて作図できる。 

ニュートンの証明

図2:平行四辺形の速度

準備: 速度の平行四辺形

図2のような平行四辺形ABCDを考える。例えば動点Pが辺AB上を点Aから点Bまで一定の速度で移動し、辺ABも動点Pが点Aから点Bに移動するのにかかるのと同じ時間をかけて辺DCの位置まで移動すると仮定する。このとき、辺ABと辺DCは常に平行を保つとする。この2つの動きを併せると、動点Pは対角線AC上を点Aから点Cまで移動することになる。ここで、一定時間における変位は速度の尺度を持つことに注目する。今の状況の場合、ABの長さはABに沿った動点Pの速度を表すし、ADの長さは辺ABが辺ADに沿って移動する速度を現していることになる。また、ACの長さは直線ACに沿って移動する動点Pの速度を表すことになる。結局、動点PがAからBに移動し、同時に辺ABが辺DCに向かって移動するこの状況の場合、動点Pの移動にのみ注目すれば、ACに沿って一定の速度で移動するのと変わらないことになる。

力の平行四辺形の証明

図1の2つのベクトルの始点に置かれた物体に、2つの力が作用しているとする。ここで、ベクトル F₁ 、 F₂ の長さは、それぞれの力が物体に生じさせる一定時間あたりの速さを、 向きは、力により物体に生じた速度の方向を現しているとする。 それぞれの力は、他方の力が働いているかどうかとは無関係に始点に置かれた物体に、それぞれのちからによる速度を生じさせる。一定時間が経てば、物体は2つの力によって生じた2つの速度を持つことになる。よって、「速度の平行四辺形」を用いると、この物体に生じる速度は図1のF{sub}net{/sub}に他ならない。ニュートンの第二法則によれば、このベクトルは速度を生じる力も現しているので、2つの力はF1 、 F2 はF{sub}net{/sub}と同等であることがわかる。

なめらかな斜面上の物体に働く力の合力を、平行四辺形を使って求める。期待通りこの方法で求まった合力(二重矢印)は斜面を下る向きに作用し、その向きに物体を加速させるものであることがわかる。

力の平行四辺形の代数的な証明

力は空間ベクトルあるいはの元としてモデル化できる。最初の仮定として、2つの力が作用することで、別の1つの力が働いているように見えることがあり、そのため任意の2つの力について異なる力である。模型化しました勢力としてユークリッドベクター員 ${\displaystyle }$ます。 当初の仮説は、その力は他の力、その他の二つの力 ${\displaystyle }$ あ力 ${\displaystyle }$ます。 い可換性を備え、これらの力を用いて行うのない事項 ${\displaystyle }$ます。

議論

力の平行四辺形の数学的な証明は、一般には数学的な正しさのために受け入れられていない。さまざまな証明が生み出され(特にDuchaylaによるものやポアソンによるもの)たが、これらに異議を唱えるものもいる。力の平行四辺形が正しいことに疑問があるのではなく、「なぜ」正しいのかということが議論されているのだ。 今日では力の平行四辺形は経験的事実として受け入れられており、ニュートンの第一法則には還元されない。

関連項目

• Newton's Mathematical Principles of Natural Philosophy, Axioms or Laws of Motion, Corollary I, at Wikisource
• 空間ベクトル
• 合力

参考文献

[[Category:力 (自然科学)]] [[Category:ベクトル解析]]