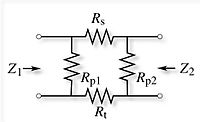
アッテネータの真数電圧減衰量を
α
=
V
1
/
V
2
≥
1
{\displaystyle \alpha =V_{1}/V_{2}\geq 1}
A
=
20
log
(
V
1
/
V
2
)
=
10
log
(
P
1
/
P
2
)
{\displaystyle A=20\log(V_{1}/V_{2})=10\log(P_{1}/P_{2})\,}
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
P
1
{\displaystyle P_{1}}
P
2
{\displaystyle P_{2}}
α
=
2
{\displaystyle \alpha ={\sqrt {2}}}
α
2
=
2
{\displaystyle \alpha ^{2}=2}
Assuming attenuation in voltage is
α
=
V
1
/
V
2
≥
1
{\displaystyle \alpha =V_{1}/V_{2}\geq 1}
A
=
20
log
(
V
1
/
V
2
)
=
10
log
(
P
1
/
P
2
)
{\displaystyle A=20\log(V_{1}/V_{2})=10\log(P_{1}/P_{2})\,}
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
P
1
{\displaystyle P_{1}}
P
2
{\displaystyle P_{2}}
α
=
2
{\displaystyle \alpha ={\sqrt {2}}}
α
2
=
2
{\displaystyle \alpha ^{2}=2}
π
{\displaystyle \pi }
{
Z
1
=
R
p
1
∥
(
R
s
+
R
p
2
∥
Z
2
)
Z
2
=
R
p
2
∥
(
R
s
+
R
p
1
∥
Z
1
)
α
=
V
1
V
2
=
P
1
P
2
≥
0
{\displaystyle {\begin{cases}Z_{1}=R_{p1}\parallel (R_{s}+R_{p2}\parallel Z_{2})\\Z_{2}=R_{p2}\parallel (R_{s}+R_{p1}\parallel Z_{1})\\\alpha ={\frac {V_{1}}{V_{2}}}={\sqrt {\frac {P_{1}}{P_{2}}}}\geq 0\end{cases}}}
を解くことにより得られる。+ と
∥
{\displaystyle \parallel }
Y-Δ変換 などの方法により得ることもできる。
以下では入出力インピーダンス比を
β
2
=
Z
1
/
Z
2
{\displaystyle \beta ^{2}=Z_{1}/Z_{2}\,}
Where, operators + and
∥
{\displaystyle \parallel }
β
2
=
Z
1
/
Z
2
{\displaystyle \beta ^{2}=Z_{1}/Z_{2}\,}
π型平衡アッテネータ 平衡・非対称の場合
{
R
p
1
=
α
2
−
1
α
2
+
1
−
2
α
β
Z
1
R
p
2
=
α
2
−
1
α
2
+
1
−
2
α
/
β
Z
2
R
s
u
=
R
s
l
=
α
2
−
1
4
α
Z
1
Z
2
{\displaystyle {\begin{cases}R_{p1}={\frac {\alpha ^{2}-1}{\alpha ^{2}+1-2\alpha \beta }}Z_{1}\\R_{p2}={\frac {\alpha ^{2}-1}{\alpha ^{2}+1-2\alpha /\beta }}Z_{2}\\R_{su}=R_{sl}={\frac {\alpha ^{2}-1}{4\alpha }}{\sqrt {Z_{1}Z_{2}}}\end{cases}}}
R
P
1
,
R
P
2
{\displaystyle R_{P1},R_{P2}}
Z
1
≥
Z
2
{\displaystyle Z_{1}\geq Z_{2}}
β
≥
1
{\displaystyle \beta \geq 1}
α
=
β
+
β
2
−
1
{\displaystyle \alpha =\beta +{\sqrt {\beta ^{2}-1}}}
で
R
p
1
=
∞
{\displaystyle R_{p1}=\infty }
Z
2
≥
Z
1
{\displaystyle Z_{2}\geq Z_{1}}
0
≤
β
≤
1
{\displaystyle 0\leq \beta \leq 1}
α
=
β
−
1
+
β
−
2
−
1
{\displaystyle \alpha =\beta ^{-1}+{\sqrt {\beta ^{-2}-1}}}
で
R
p
2
=
∞
{\displaystyle R_{p2}=\infty }
である。
平衡・対称の場合 上式において
Z
=
Z
1
=
Z
2
{\displaystyle Z=Z_{1}=Z_{2}}
β
=
1
{\displaystyle \beta =1}
{
R
p
1
=
R
p
2
=
α
+
1
α
−
1
⋅
Z
R
s
u
=
R
s
l
=
α
2
−
1
4
α
⋅
Z
{\displaystyle {\begin{cases}R_{p1}=R_{p2}={\frac {\alpha +1}{\alpha -1}}\cdot Z\\R_{su}=R_{sl}={\frac {\alpha ^{2}-1}{4\alpha }}\cdot Z\end{cases}}}
π型不平衡アッテネータ 不平衡・非対称の場合 π型平衡アッテネータの定数に対して
R
s
=
R
s
u
+
R
s
l
{\displaystyle R_{s}=R_{su}+{R_{s}l}}
{
R
p
1
=
α
2
−
1
α
2
+
1
−
2
α
β
Z
1
R
p
2
=
α
2
−
1
α
2
+
1
−
2
α
/
β
Z
2
R
s
=
α
2
−
1
2
α
z
1
z
2
{\displaystyle {\begin{cases}R_{p1}={\frac {\alpha ^{2}-1}{\alpha ^{2}+1-2\alpha \beta }}Z_{1}\\R_{p2}={\frac {\alpha ^{2}-1}{\alpha ^{2}+1-2\alpha /\beta }}Z_{2}\\R_{s}={\frac {\alpha ^{2}-1}{2\alpha }}{\sqrt {z_{1}z_{2}}}\end{cases}}}
ただし、
R
P
1
,
R
P
2
{\displaystyle R_{P1},R_{P2}}
Z
1
≥
Z
2
{\displaystyle Z_{1}\geq Z_{2}}
β
≥
1
{\displaystyle \beta \geq 1}
α
=
β
+
β
2
−
1
{\displaystyle \alpha =\beta +{\sqrt {\beta ^{2}-1}}}
で
R
p
1
=
∞
{\displaystyle R_{p1}=\infty }
Z
2
≥
Z
1
{\displaystyle Z_{2}\geq Z_{1}}
0
≤
β
≤
1
{\displaystyle 0\leq \beta \leq 1}
α
=
β
−
1
+
β
−
2
−
1
{\displaystyle \alpha =\beta ^{-1}+{\sqrt {\beta ^{-2}-1}}}
で
R
p
2
=
∞
{\displaystyle R_{p2}=\infty }
である。
不平衡・対称の場合 上式において
Z
=
Z
1
=
Z
2
{\displaystyle Z=Z_{1}=Z_{2}}
{
R
p
1
=
R
p
2
=
α
+
1
α
−
1
⋅
Z
R
s
=
α
2
−
1
2
α
⋅
Z
{\displaystyle {\begin{cases}R_{p1}=R_{p2}={\frac {\alpha +1}{\alpha -1}}\cdot Z\\R_{s}={\frac {\alpha ^{2}-1}{2\alpha }}\cdot Z\end{cases}}}
T型不平衡アッテネータ
{
R
s
1
=
R
s
2
=
R
p
=
{\displaystyle {\begin{cases}R_{s1}=\\R_{s2}=\\R_{p}=\end{cases}}}
T型平衡アッテネータ π型不平衡回路をY-Δ変換 変換することにより、
{
R
s
u
1
=
R
s
u
2
=
R
s
l
1
=
R
s
l
2
=
R
p
=
{\displaystyle {\begin{cases}R_{su1}=R_{su2}=\\R_{sl1}=R_{sl2}=\\R_{p}=\end{cases}}}