利用者:Nova replet laetitia/sandbox/宇宙・物理・自然科学/電子配置

ここはNova replet laetitiaさんの利用者サンドボックスです。編集を試したり下書きを置いておいたりするための場所であり、百科事典の記事ではありません。ただし、公開の場ですので、許諾されていない文章の転載はご遠慮ください。

記事がある程度できあがったら、編集方針を確認して、新規ページを作成しましょう。

量子数と軌道

原子を構成している電子の振舞いは原子核による静電ポテンシャル中の3次元シュレーディンガー方程式を解くことで得られる（特に水素原子におけるシュレーディンガー方程式の解は解析的に解ける）。

量子力学では運動量 $p$ を

p=-i\hbar {\frac {\partial }{\partial x}}

と演算子で書く(正準量子化)。 $\hbar$ は換算プランク定数、 $i$ は虚数。よってハミルトニアン $H$ は

H=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {1}{2}}kx^{2}\right]

となる。

1次元の量子的な調和振動子についての時間依存しないシュレーディンガー方程式は、以下のように書ける。

\left[-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {1}{2}}kx^{2}\right]\phi (x)=E\phi

この方程式は解析的に解くことができ、その解（エネルギー固有状態）はエルミート多項式 $H_{n}$ を使って以下のように表される。

\phi _{n}(x)=AH_{n}(\xi )\exp \left(-{\frac {\xi ^{2}}{2}}\right)

ただし、 $\xi ={\sqrt {\frac {m\omega }{\hbar }}}x$ 、 $A$ は規格化定数で次式で与えられる。

A={\sqrt {{\frac {1}{n!2^{n}}}{\sqrt {\frac {m\omega }{\pi \hbar }}}}}

また、エルミート多項式 $H_{n}$ は

H_{n}(x)=(-1)^{n}\exp \left(x^{2}\right){\frac {\mathrm {d} ^{n}}{\mathrm {d} x^{n}}}\exp \left(-x^{2}\right)

で定義される。具体例として $n=0,1,2$ の場合を示すと

H_{0}=1

H_{1}=2x

H_{2}=4x^{2}+2

である。基底状態（ $n=0$ ）のエネルギー固有状態はガウス波束であり、 $x=0$ 付近に局在している。エネルギー固有値は次のようになる。

E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right)\qquad (n=0,1,2,...)

つまりエネルギー準位は $\hbar \omega$ という均等な間隔で並ぶ。 $n=0$ の状態は零点振動、そのエネルギー固有値 $E_{n}={\frac {1}{2}}\hbar \omega$ は零点エネルギーと呼ばれる。

量子調和振動子の波動関数はエルミート多項式 H_n を使って以下のように書ける。エルミート多項式は、

\psi _{n}(x)=\left(2^{n}n!{\sqrt {\pi }}\right)^{-{\frac {1}{2}}}e^{-{\frac {x^{2}}{2}}}H_{n}(x)=(-1)^{n}\left(2^{n}n!{\sqrt {\pi }}\right)^{-{\frac {1}{2}}}e^{\frac {x^{2}}{2}}{\frac {\mathrm {d} ^{n}}{\mathrm {d} x^{n}}}e^{-x^{2}}.

\Psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)

where $n = 0,1,2,...$ .

原子を構成している電子の振舞いは原子核による静電ポテンシャル中の3次元シュレーディンガー方程式を解くことで得られる（特に水素原子におけるシュレーディンガー方程式の解は解析的に解ける）。電子のとり得る軌道は主量子数 n、方位量子数 l、磁気量子数 m の3つによって指定される。

主量子数 n は軌道の大きさとエネルギーを決定している。1, 2, 3, ... と整数値をとり、これは電子殻 K殻、L殻、M殻、…に対応している。
方位量子数 l は軌道の形を決定している。0, 1, 2, ..., n−1 の整数値をとる。これはs軌道、p軌道、d軌道、f軌道、g軌道…に対応している。
磁気量子数mは各軌道を決定している。−l, −l+1, ..., 0, ..., l−1, l の整数値をとる。

例えば、主量子数2、方位量子数1の軌道を総称して2p軌道と呼ぶ。2p軌道は −1, 0, 1 の3つの磁気量子数をとり得るが、これらに対応して、2p_x, 2p_y, 2p_z の異なる配位をもつ3つの軌道が存在する。

電子のとり得る軌道は主量子数 n、方位量子数 l、磁気量子数 m の3つによって指定される。

主量子数 n は軌道の大きさとエネルギーを決定している。1, 2, 3, ... と整数値をとり、これは電子殻 K殻、L殻、M殻、…に対応している。
方位量子数 l は軌道の形を決定している。0, 1, 2, ..., n−1 の整数値をとる。これはs軌道、p軌道、d軌道、f軌道、g軌道…に対応している。
磁気量子数mは各軌道を決定している。−l, −l+1, ..., 0, ..., l−1, l の整数値をとる。

例えば、主量子数2、方位量子数1の軌道を総称して2p軌道と呼ぶ。2p軌道は −1, 0, 1 の3つの磁気量子数をとり得るが、これらに対応して、2p_x, 2p_y, 2p_z の異なる配位をもつ3つの軌道が存在する。

量子数と軌道と電子対

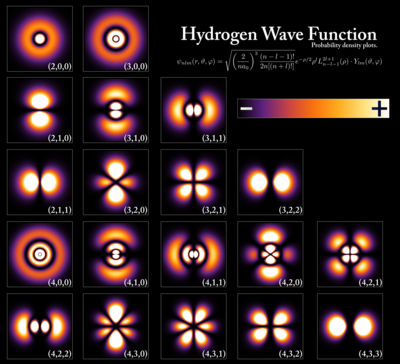
The wave functions of an electron in a Hydrogen atom are expressed in terms of spherical harmonics and generalized Laguerre polynomials (these are defined differently by different authors—see main article on them and the hydrogen atom).

It is convenient to use spherical coordinates, and the wavefunction can be separated into functions of each coordinate,^[1]

\Psi _{n\ell m}(r,\theta ,\phi )=R(r)\,\,Y_{\ell }^{m}\!(\theta ,\phi )

where $R$ are radial functions and $Y m ℓ (θ, φ)$ are spherical harmonics of degree $ℓ$ and order $m$ . This is the only atom for which the Schrödinger equation has been solved exactly. Multi-electron atoms require approximative methods. The family of solutions is:^[2]

\Psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )

where $a 0 = 4 πε 0 ħ 2 / m e e 2$ is the Bohr radius, $L 2 ℓ + 1 n - ℓ - 1$ are the generalized Laguerre polynomials of degree $n - ℓ - 1$ , $n = 1, 2, ...$ is the principal quantum number, $ℓ = 0, 1, ... n - 1$ the azimuthal quantum number, $m = - ℓ, - ℓ + 1, ..., ℓ - 1, ℓ$ the magnetic quantum number. Hydrogen-like atoms have very similar solutions.

This solution does not take into account the spin of the electron.

このように電子の配置は、3つの量子数(n、l、m）で区別される軌道に対応付けられる。そして電子の属する軌道の種類に応じて、電子も分類されて呼称される。

s電子 - s軌道上の電子。1s電子、2s電子、3s電子、4s電子、5s電子、6s電子、7s電子が存在する。
p電子 - p軌道上の電子。2p電子、3p電子、4p電子、5p電子、6p電子、7p電子が存在する。
d電子 - d軌道上の電子。3d電子、4d電子、5d電子、6d電子が存在する。
f電子 - f軌道上の電子。4f電子、5f電子が存在する。

さらに、電子はフェルミ粒子であり、複数のフェルミ粒子が1つの軌道には、お互いに逆向きのスピンをもつ2個の電子しか入ることができない（「パウリの排他原理」）。このように軌道が2つの電子によって占有された状態を電子対と呼ぶ。

粒子を表す波動関数φ が位置 x 存在するとき、これを φ(x) で表すと、波動関数

\int |\Phi (x)|^{2}dx=\phi (y)=-\phi (y)\phi (x)

同じ粒子が異なる位置 y でも存在して 2 粒子系をとるとき、フェルミ粒子は

\phi (x)\phi (y)=-\phi (y)\phi (x)

という性質をもつ。2 粒子系の波動関数 ψ は

\int |\Psi |^{2}d\mathbf {r} =\iint \psi (x,y)\phi (x)\phi (y)dxdy=-\iint \psi (y,x)\phi (y)\phi (x)dxdy

これが正の値をとるためには、

\psi (x,y)=-\psi (y,x)

もし同じ軌道に電子が2つはいると、

\psi (x,x)=-\psi (x,x)=0

となり

\iint \psi (x,x^{*})\phi (x)\phi (x^{*})dxdx^{*}=-\iint \psi (x^{*},x)\phi (x^{*})\phi (x)dxdx^{*}

おなじ軌道に別の粒子が存在してこれをχ で表すと、フェルミ粒子では

{\phi }(x_{1},x_{2})=-{\phi }(x_{2},x_{1})

とならなくてはならないから、すなわち、2つのフェルミ粒子があってそれぞれの1粒子の波動関数が φ, χ と表せるなら、2つのフェルミ粒子の全波動関数は単に

\psi (x_{1},x_{2})=\phi (x_{1})\chi (x_{2})

ではなく、この入れ替えについての性質から

\psi (x_{1},x_{2})=\phi (x_{1})\chi (x_{2})-\phi (x_{2})\chi (x_{1})

と表されなくてはならない。

仮に2つのフェルミ粒子が同じ1粒子波動関数をとると

\psi (x_{1},x_{2})=\phi (x_{1})\phi (x_{2})-\phi (x_{2})\phi (x_{1})=0

2つのフェルミ粒子が同じ状態にある時は、ψ = 0という結果が得られる。すなわち、フェルミ粒子は、1つの体系内で2個の粒子がある同じ量子状態になることが許されない。すなわち、フェルミ粒子はパウリの排他原理に従う。この規則から導かれる熱平衡状態にある同種のフェルミ粒子からなる体系が従う量子統計をフェルミ=ディラック統計という。

言い換えると、2p軌道には最大6個の電子が収容される。同様に3d, 4d等のd軌道には最大10個、4f等のf軌道には最大14個の電子が収容される。

以上をまとめると下表のようになる。

量子数と軌道の対応

量子数と軌道の対応^[3]
ℓ	ℓ $=0$ $(s軌道)$	ℓ $=1$ $(p軌道)$			ℓ $=2$ $(d軌道)$					ℓ $=3$ $(f軌道)$
ℓ	s亜殻の最大電子数 2 p亜殻（ℓ≧1）の最大電子数 6 d亜殻（ℓ≧2）の最大電子数 10 f亜殻（ℓ≧3）の最大電子数 14
$m$	$m =1$	$m =2$	$m =\pm1$		$m =0$	$m =\pm1$		$m =\pm2$		$m =0$	$m =\pm1$		$m =\pm2$		$m =\pm3$
最大電子数	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
$n =1$ $(K殻)$	$1s$
$n =1$ $(K殻)$	K殻の最大電子数 = 2(1s軌道) 第1周期元素の貴ガスヘリウム（He）の電子数：2(1s軌道)
$n =2$ $(L殻)$	$2s$	$2p z$	$2p x$	$2p y$
$n =2$ $(L殻)$	L殻の最大電子数 2(2s軌道)+6(2p軌道) = 8 第2周期元素の貴ガスネオン（Ne）の電子数：2(=[He])+2(2s軌道)+6(2p軌道) = 10
$n =3$ $(M殻)$	$3s$	$3p z$	$3p x$	$3p y$	$3d z 2$	$3d xz$	$3d yz$	$3d xy$	$3d x 2 -y 2$
$n =3$ $(M殻)$	M殻の最大電子数 2(3s軌道)+6(3p軌道)+10(3d軌道) = 18 第3周期元素の貴ガスアルゴン（Ar）の電子数：10(=[Ne])+2(3s軌道)+6(3p軌道) = 18
$n =4$ $(N殻)$	$4s$	$4p z$	$4p x$	$4p y$	$4d z 2$	$4d xz$	$4d yz$	$4d xy$	$4d x 2 -y 2$	$4f z 3$	$4f xz 2$	$4f yz 2$	$4f xyz$	$4f z(x 2 -y 2)$	$4f x(x 2 -3y 2)$	$4f y(3x 2 -y 2)$
$n =4$ $(N殻)$	N殻の最大電子数 2(4s軌道)+6(4p軌道)+10(4d軌道)+14(4f軌道) = 32 第4周期元素の貴ガスクリプトン（Kr）の電子数：18(=[Ar])+2(4s軌道)+10(3d軌道)+6(4p軌道) = 36
ℓ	ℓ $=0$ $(s軌道)$	ℓ $=1$ $(p軌道)$			ℓ $=2$ $(d軌道)$					ℓ $=3$ $(f軌道)$
$m$	$m =1$	$m =2$	$m =\pm1$		$m =0$	$m =\pm1$		$m =\pm2$		$m =0$	$m =\pm1$		$m =\pm2$		$m =\pm3$
$n= 5$ $(O殻)$	$5s$	$5p z$	$5p x$	$5p y$	$5d z 2$	$5d xz$	$5d yz$	$5d xy$	$5d x 2 -y 2$	$5f z 3$ . . .	$5f xz 2$ . . .	$5f yz 2$ . . .	$5f xyz$ . . .	$5f z(x 2 -y 2)$ . . .	$5f x(x 2 -3y 2)$ . . .	$5f y(3x 2 -y 2)$ . . .
$n= 5$ $(O殻)$	O殻の最大電子数 2(5s軌道)+6(5p軌道)+10(5d軌道)+14(5f軌道)+18(5g軌道) = 50 第5周期元素の貴ガスキセノン（Xe）の電子数：36(=[Kr])+2(5s軌道)+10(4d軌道)+6(5p軌道) = 54
$n = 6$ $(P殻)$	$6s$	$6p z$	$6p x$	$6p y$	$6d z 2$	$6d xz$	$6d yz$	$6d xy$	$6d x 2 -y 2$	$6f z 3$ . . .	$6f xz 2$ . . .	$6f yz 2$ . . .	$6f xyz$ . . .	$6f z(x 2 -y 2)$ . . .	$6f x(x 2 -3y 2)$ . . .	$6f y(3x 2 -y 2)$ . . .
$n = 6$ $(P殻)$	P殻の最大電子数 2(6s軌道)+6(6p軌道)+10(6d軌道)+14(6f軌道)+18(6g軌道)+22(6h軌道) = 72 第6周期元素の貴ガスラドン（Rn）の電子数：54(=[Xn])+2(6s軌道)+14(4f軌道)+10(5d軌道)+6(6p軌道) = 86
$n= 7$ $(Q殻)$	$7s$	$7p z$ . . .	$7p x$ . . .	$7p y$ . . .	$7d z 2$ . . .	$7d xz$ . . .	$7d yz$ . . .	$7d xy$ . . .	$7d x 2 -y 2$ . . .	$7f z 3$ . . .	$7f xz 2$ . . .	$7f yz 2$ . . .	$7f xyz$ . . .	$7f z(x 2 -y 2)$ . . .	$7f x(x 2 -3y 2)$ . . .	$7f y(3x 2 -y 2)$ . . .
$n= 7$ $(Q殻)$	Q殻の最大電子数 2(7s軌道)+6(7p軌道)+10(7d軌道)+14(7f軌道)+18(7g軌道)+22(7h軌道)+26(7i軌道) = 98 第7周期元素の推定貴ガスオガネソン（Og）の推定電子数：86([Rn])+2(7s軌道)+14(5f軌道)+10(6d軌道)+6(7p軌道) = 118

原子中の電子の5g軌道は第8周期元素において現れると予測されている。

O殻( *$n=5$* )における量子数とg軌道の対応^[4]
ℓ	ℓ $=4$ $(g軌道)$
ℓ	g亜殻（ℓ≧4）の最大電子数 18
$m$	$m =0$	$m =\pm1$		$m =\pm2$		$m =\pm3$		$m =\pm4$
最大電子数	2	2	2	2	2	2	2	2	2
$n =5$ $(O殻)$	$5g z 4$	$5g xz 3$	$5g yz 3$	$5g z 2 (x 2 -y 2)$	$5g xyz 2$	$5g zx 3$	$5g zy 3$	$5g x 4 +y 4$	$5g xy(x 2 -y 2)$
$n =5$ $(O殻)$	第8周期元素の推定貴ガス E168（Uho）の推定電子数： 118([Og])+2(8s軌道)+18(5g軌道)+14(6f軌道)+10(7d軌道)+6(8p軌道) = 168

しかしg軌道はd軌道やf軌道以上に相対論効果が著しくなるため理論通りの電子配置をとるかどうかはまだ明らかでなく、電子配置が定まらないため第8周期以降、119番以降の元素は、いまだにさまざまな拡張周期表が提案されている段階にすぎない。また原子核も不安定で短時間で崩壊してしまうため、仮に物理的には人工的な元素合成ができたとしても、化学的性質の同定は極めて困難と推測されている。

^ Physics for Scientists and Engineers – with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7
^ David Griffiths (2008). Introduction to elementary particles. Wiley-VCH. pp. 162–. ISBN 978-3-527-40601-2 27 June 2011閲覧。
^ “Grand Orbital Table”. 2018年8月4日閲覧。
^ McCaw, Charles S. (2015). Orbitals: With Applications in Atomic Spectra. p. 51. ISBN 978-1783264131

[1] Physics for Scientists and Engineers – with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7

[2] David Griffiths (2008). Introduction to elementary particles. Wiley-VCH. pp. 162–. ISBN 978-3-527-40601-2 27 June 2011閲覧。

[3] “Grand Orbital Table”. 2018年8月4日閲覧。

[4] McCaw, Charles S. (2015). Orbitals: With Applications in Atomic Spectra. p. 51. ISBN 978-1783264131

[1]

[2]

[3]

[4]