利用者:Nova replet laetitia/sandbox/技術・情報/クォータニアンと空間回転

クォータニオンと空間回転

Unit quaternions, also known as versors, provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more compact, more numerically stable, and more efficient. Quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites and crystallographic texture analysis.

When used to represent rotation, unit quaternions are also called rotation quaternions. When used to represent an orientation (rotation relative to a reference coordinate system), they are called orientation quaternions or attitude quaternions. 単位 四元数は、バーサ（versors）としても知られており、3次元でオブジェクトの向きや回転を表現するのに便利な数学的記法を提供します。オイラー角と比較すると、ジンバルロックの問題を回避し、回避するのが簡単です。回転行列と比較すると、よりコンパクトで、数値的に安定し、より効率的です。クォータニオンは、コンピュータグラフィックス[1]、コンピュータビジョン、ロボット[2]、ナビゲーション、分子動力学、飛行力学、[3] 軌道力学の衛星[4]及び 結晶学的テクスチャ解析。[5]

回転を表現するために使用すると、単位四元数は回転四元数とも呼ばれます。方位（基準座標系に対する相対的な回転）を表すために使用されるとき、方位四元数または姿勢四元数と呼ばれます。

オイラー軸と角度で表される回転の視覚化。Using quaternion as rotations

A visualization of a rotation represented by an Euler axis and angle.

In 3-dimensional space, according to Euler's rotation theorem, any rotation or sequence of rotations of a rigid body or coordinate system about a fixed point is equivalent to a single rotation by a given angle θ about a fixed axis (called the Euler axis) that runs through the fixed point. The Euler axis is typically represented by a unit vector u→. Therefore, any rotation in three dimensions can be represented as a combination of a vector u→ and a scalar θ. Quaternions give a simple way to encode this axis–angle representation in four numbers, and can be used to apply the corresponding rotation to a position vector, representing a point relative to the origin in R³.

A Euclidean vector such as (2, 3, 4) or (a_x, a_y, a_z) can be rewritten as 2 i + 3 j + 4 k or a_x i + a_y j + a_z k, where i, j, k are unit vectors representing the three Cartesian axes. A rotation through an angle of θ around the axis defined by a unit vector

${\vec {u}}=(u_{x},u_{y},u_{z})=u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k}$

can be represented by a quaternion. This can be done using an extension of Euler's formula:

$\mathbf {q} =e^{{\frac {\theta }{2}}{(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )}}=\cos {\frac {\theta }{2}}+(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\sin {\frac {\theta }{2}}$

It can be shown that the desired rotation can be applied to an ordinary vector $\mathbf {p} =(p_{x},p_{y},p_{z})=p_{x}\mathbf {i} +p_{y}\mathbf {j} +p_{z}\mathbf {k}$ in 3-dimensional space, considered as a quaternion with a real coordinate equal to zero, by evaluating the conjugation of p by q:

$\mathbf {p'} =\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}$

using the Hamilton product, where p′ = (p_x′, p_y′, p_z′) is the new position vector of the point after the rotation. In a programmatic implementation, this is achieved by constructing a quaternion whose vector part is p and real part equals zero and then performing the quaternion multiplication. The vector part of the resulting quaternion is the desired vector p′.

Mathematically, this operation carries the set of all "pure" quaternions p (those with real part equal to zero)—which constitute a 3-dimensional space among the quaternions—into itself, by the desired rotation about the axis u, by the angle θ. (Each real quaternion is carried into itself by this operation. But for the purpose of rotations in 3-dimensional space, we ignore the real quaternions.)

The rotation is clockwise if our line of sight points in the same direction as u→.

In this instance, q is a unit quaternion and

$\mathbf {q} ^{-1}=e^{-{\frac {\theta }{2}}{(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )}}=\cos {\frac {\theta }{2}}-(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\sin {\frac {\theta }{2}}.$

It follows that conjugation by the product of two quaternions is the composition of conjugations by these quaternions: If p and q are unit quaternions, then rotation (conjugation) by pq is

$\mathbf {pq} {\vec {v}}(\mathbf {pq} )^{-1}=\mathbf {pq} {\vec {v}}\mathbf {q} ^{-1}\mathbf {p} ^{-1}=\mathbf {p} (\mathbf {q} {\vec {v}}\mathbf {q} ^{-1})\mathbf {p} ^{-1}$,

which is the same as rotating (conjugating) by q and then by p. The scalar component of the result is necessarily zero.

The quaternion inverse of a rotation is the opposite rotation, since $\mathbf {q} ^{-1}(\mathbf {q} {\vec {v}}\mathbf {q} ^{-1})\mathbf {q} ={\vec {v}}$. The square of a quaternion rotation is a rotation by twice the angle around the same axis. More generally qⁿ is a rotation by n times the angle around the same axis as q. This can be extended to arbitrary real n, allowing for smooth interpolation between spatial orientations; see Slerp.

Two rotation quaternions can be combined into one equivalent quaternion by the relation:

$\mathbf {q} '=\mathbf {q} _{2}\mathbf {q} _{1}$

in which q′ corresponds to the rotation q₁ followed by the rotation q₂. (Note that quaternion multiplication is not commutative.) Thus, an arbitrary number of rotations can be composed together and then applied as a single rotation.

Example

The conjugation operation

A rotation of 120° around the first diagonal permutes i, j, and k cyclically.

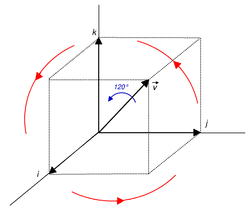
Conjugating p by q refers to the operation p ↦ q p q⁻¹.

Consider the rotation f around the axis ${\vec {v}}=\mathbf {i} +\mathbf {j} +\mathbf {k}$, with a rotation angle of 120°, or 2π/3 radians.

$\alpha ={\dfrac {2\pi }{3}}$

p ↦ q p for q = 1 + i + j + k/2 on the unit 3-sphere. Note this one-sided (namely, left) multiplication yields a 60° rotation of quaternions

The length of v→ is √3, the half angle is π/3 (60°) with cosine 1/2, (cos 60° = 0.5) and sine √3/2, (sin 60° ≈ 0.866). We are therefore dealing with a conjugation by the unit quaternion

${\begin{array}{lll}u&=&\cos {\dfrac {\alpha }{2}}+\sin {\dfrac {\alpha }{2}}\cdot {\dfrac {1}{\|{\vec {v}}\|}}{\vec {v}}\\&=&\cos {\dfrac {\pi }{3}}+\sin {\dfrac {\pi }{3}}\cdot {\dfrac {1}{\sqrt {3}}}{\vec {v}}\\&=&{\dfrac {1}{2}}+{\dfrac {\sqrt {3}}{2}}\cdot {\dfrac {1}{\sqrt {3}}}{\vec {v}}\\&=&{\dfrac {1}{2}}+{\dfrac {\sqrt {3}}{2}}\cdot {\dfrac {\mathbf {i} +\mathbf {j} +\mathbf {k} }{\sqrt {3}}}\\&=&{\dfrac {1+\mathbf {i} +\mathbf {j} +\mathbf {k} }{2}}\end{array}}$

If f is the rotation function,

$f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )=u(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )u^{-1}$

It can be proven that the inverse of a unit quaternion is obtained simply by changing the sign of its imaginary components. As a consequence,

$u^{-1}={\dfrac {1-\mathbf {i} -\mathbf {j} -\mathbf {k} }{2}}$

and

$f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )={\dfrac {1+\mathbf {i} +\mathbf {j} +\mathbf {k} }{2}}(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} ){\dfrac {1-\mathbf {i} -\mathbf {j} -\mathbf {k} }{2}}$

This can be simplified, using the ordinary rules for quaternion arithmetic, to

$f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )=c\mathbf {i} +a\mathbf {j} +b\mathbf {k}$

As expected, the rotation corresponds to keeping a cube held fixed at one point, and rotating it 120° about the long diagonal through the fixed point (observe how the three axes are permuted cyclically).

Quaternion-derived rotation matrix

A quaternion rotation $\mathbf {p'} =\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}$ (with $\mathbf {q} =q_{r}+q_{i}\mathbf {i} +q_{j}\mathbf {j} +q_{k}\mathbf {k}$) can be algebraically manipulated into a matrix rotation $\mathbf {p'} =\mathbf {Rp}$, where R is the rotation matrix given by:

${\begin{aligned}\mathbf {R} &={\begin{bmatrix}1-2s(q_{j}^{2}+q_{k}^{2})&2s(q_{i}q_{j}-q_{k}q_{r})&2s(q_{i}q_{k}+q_{j}q_{r})\\2s(q_{i}q_{j}+q_{k}q_{r})&1-2s(q_{i}^{2}+q_{k}^{2})&2s(q_{j}q_{k}-q_{i}q_{r})\\2s(q_{i}q_{k}-q_{j}q_{r})&2s(q_{j}q_{k}+q_{i}q_{r})&1-2s(q_{i}^{2}+q_{j}^{2})\end{bmatrix}}\end{aligned}}$

Here $s=||q||^{-2}$ and if q is a unit quaternion, $s=1$

This can be obtained by using vector calculus and linear algebra if we express $\mathbf {p}$ and $\mathbf {q}$ as scalar and vector parts and use the formula for the multiplication operation in the equation $\mathbf {p'} =\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}$. If we write $\mathbf {p}$ as $(0,\ \mathbf {p} )$, $\mathbf {p} '$ as $(0,\ \mathbf {p} ')$ and $\mathbf {q}$ as $(q_{r},\ \mathbf {v} )$, where $\mathbf {v} =(q_{i},q_{j},q_{k})$, our equation turns into $(0,\ \mathbf {p} ')=(q_{r},\ \mathbf {v} )(0,\ \mathbf {p} )s(q_{r},\ -\mathbf {v} )$. By using the formula for multiplication of two quaternions that are expressed as scalar and vector parts,

$(r_{1},\ {\vec {v}}_{1})(r_{2},\ {\vec {v}}_{2})=(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2}),$

this equation can be rewritten as

${\begin{aligned}(0,\ \mathbf {p} ')=&\ ((q_{r},\ \mathbf {v} )(0,\ \mathbf {p} ))s(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ (q_{r}\times 0-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +0\mathbf {v} +\mathbf {v} \times \mathbf {p} )s(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} q_{r}-(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\cdot (-\mathbf {v} ),\ (-\mathbf {v} \cdot \mathbf {p} )(-\mathbf {v} )+q_{r}(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )+(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\times (-\mathbf {v} ))\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} q_{r}+q_{r}\mathbf {v} \cdot \mathbf {p} ,\ \mathbf {v} (\mathbf {v} \cdot \mathbf {p} )+q_{r}^{2}\mathbf {p} +q_{r}\mathbf {v} \times \mathbf {p} +\mathbf {v} \times (q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} ))\\(0,\ \mathbf {p} ')=&\ (0,\ s(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2})\mathbf {p} ),\end{aligned}}$

where $\otimes$ denotes the outer product, $\mathbf {I}$ is the identity matrix and $[\mathbf {v} ]_{\times }$ is the transformation matrix that when multiplied from the left with a vector $\mathbf {u}$ gives the cross product $\mathbf {v} \times \mathbf {u}$.

Since $\mathbf {p} '=\mathbf {R} \mathbf {p}$, we can identify $\mathbf {R}$ as $s(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2})$, which upon expansion should result in the expression written in matrix form above.

Recovering the axis-angle representation

The expression $\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}$ rotates any vector quaternion $\mathbf {p}$ around an axis given by the vector $\mathbf {a}$ by the angle $\theta$, where $\mathbf {a}$ and $\theta$ depends on the quaternion $\mathbf {q} =q_{r}+q_{i}\mathbf {i} +q_{j}\mathbf {j} +q_{k}\mathbf {k}$.

$\mathbf {a}$ and $\theta$ can be found from the following equations:

$(a_{x},a_{y},a_{z})\ =\ {\frac {(q_{i},q_{j},q_{k})}{\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}}}$

$\theta \ =\ 2\operatorname {atan2} \left({\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}},q_{r}\right),$

where $\mathrm {atan2}$ is the two-argument arctangent. Care should be taken when the quaternion approaches a scalar, since due to degeneracy the axis of an identity rotation is not well-defined.

The composition of spatial rotations

A benefit of the quaternion formulation of the composition of two rotations R_B and R_A is that it yields directly the rotation axis and angle of the composite rotation R_C=R_BR_A.

Let the quaternion associated with a spatial rotation R is constructed from its rotation axis S and the rotation angle φ this axis. The associated quaternion is given by,

$S=\cos {\frac {\phi }{2}}+\sin {\frac {\phi }{2}}\mathbf {S} .$

Then the composition of the rotation R_R with R_A is the rotation R_C=R_BR_A with rotation axis and angle defined by the product of the quaternions

$A=\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\mathbf {A} \quad {\text{and}}\quad B=\cos {\frac {\beta }{2}}+\sin {\frac {\beta }{2}}\mathbf {B} ,$

that is

$C=\cos {\frac {\gamma }{2}}+\sin {\frac {\gamma }{2}}\mathbf {C} ={\Big (}\cos {\frac {\beta }{2}}+\sin {\frac {\beta }{2}}\mathbf {B} {\Big )}{\Big (}\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\mathbf {A} {\Big )}.$

Expand this product to obtain

$\cos {\frac {\gamma }{2}}+\sin {\frac {\gamma }{2}}\mathbf {C} ={\Big (}\cos {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}-\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} {\Big )}+{\Big (}\sin {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}\mathbf {B} +\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\mathbf {A} +\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \times \mathbf {A} {\Big )}.$

Divide both sides of this equation by the identity, which is the law of cosines on a sphere,

$\cos {\frac {\gamma }{2}}=\cos {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}-\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} ,$

and compute

$\tan {\frac {\gamma }{2}}\mathbf {C} ={\frac {\tan {\frac {\beta }{2}}\mathbf {B} +\tan {\frac {\alpha }{2}}\mathbf {A} +\tan {\frac {\beta }{2}}\tan {\frac {\alpha }{2}}\mathbf {B} \times \mathbf {A} }{1-\tan {\frac {\beta }{2}}\tan {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} }}.$

This is Rodrigues formula for the axis of a composite rotation defined in terms of the axes of the two rotations. He derived this formula in 1840 (see page 408).

The three rotation axes A, B, and C form a spherical triangle and the dihedral angles between the planes formed by the sides of this triangle are defined by the rotation angles. Hamilton presented the component form of these equations showing that the quaternion product computes the third vertex of a spherical triangle from two given vertices and their associated arc-lengths, which is also defines an algebra for points in Elliptic geometry.

Differentiation with respect to the rotation quaternion

The rotated quaternion p'=q p q* needs to be differentiated with respect to the rotating quaternion q , when the rotation is estimated from numerical optimization. The estimation of rotation angle is an essential procedure in 3D object registration or camera calibration. The derivative can be represented using the Matrix Calculus notation.

${\begin{aligned}{\frac {\partial \mathbf {p'} }{\partial \mathbf {q} }}\equiv \left[{\frac {\partial \mathbf {p'} }{\partial q_{0}}},{\frac {\partial \mathbf {p'} }{\partial q_{x}}},{\frac {\partial \mathbf {p'} }{\partial q_{y}}},{\frac {\partial \mathbf {p'} }{\partial q_{z}}}\right]=\left[\mathbf {pq} -(\mathbf {pq} )^{*},(\mathbf {pqi} )^{*}-\mathbf {pqi} ,(\mathbf {pqj} )^{*}-\mathbf {pqj} ,(\mathbf {pqk} )^{*}-\mathbf {pqk} \right].\end{aligned}}$

A derivation can be found in .

Introduction

Quaternions

→詳細は「Quaternions」を参照

The complex numbers can be defined by introducing an abstract symbol i which satisfies the usual rules of algebra and additionally the rule i² = −1. This is sufficient to reproduce all of the rules of complex number arithmetic: for example:

$(a+b\mathbf {i} )(c+d\mathbf {i} )=ac+ad\mathbf {i} +b\mathbf {i} c+b\mathbf {i} d\mathbf {i} =ac+ad\mathbf {i} +bc\mathbf {i} +bd\mathbf {i} ^{2}=(ac-bd)+(bc+ad)\mathbf {i} .$

In the same way the quaternions can be defined by introducing abstract symbols i, j, k which satisfy the rules i² = j² = k² = i j k = −1 and the usual algebraic rules except the commutative law of multiplication (a familiar example of such a noncommutative multiplication is matrix multiplication). From this all of the rules of quaternion arithmetic follow, such as the rules on multiplication of quaternion basis elements. Using these rules, one can show that:

$(a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} )(e+f\mathbf {i} +g\mathbf {j} +h\mathbf {k} )=$

$(ae-bf-cg-dh)+(af+be+ch-dg)\mathbf {i} +(ag-bh+ce+df)\mathbf {j} +(ah+bg-cf+de)\mathbf {k} .$

The imaginary part $b\mathbf {i} +c\mathbf {j} +d\mathbf {k}$ of a quaternion behaves like a vector ${\vec {v}}=(b,c,d)$ in three dimension vector space, and the real part a behaves like a scalar in R. When quaternions are used in geometry, it is more convenient to define them as a scalar plus a vector:

$a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =a+{\vec {v}}.$

Those who have studied vectors at school might find it strange to add a number to a vector, as they are objects of very different natures, or to multiply two vectors together, as this operation is usually undefined. However, if one remembers that it is a mere notation for the real and imaginary parts of a quaternion, it becomes more legitimate. In other words, the correct reasoning is the addition of two quaternions, one with zero vector/imaginary part, and another one with zero scalar/real part:

$a+{\vec {v}}=(a,{\vec {0}})+(0,{\vec {v}}).$

We can express quaternion multiplication in the modern language of vector cross and dot products (which were actually inspired by the quaternions in the first place ). When multiplying the vector/imaginary parts, in place of the rules i² = j² = k² = ijk = −1 we have the quaternion multiplication rule:

${\vec {v}}{\vec {w}}={\vec {v}}\times {\vec {w}}-{\vec {v}}\cdot {\vec {w}},$

where:

• ${\vec {v}}{\vec {w}}$ is the resulting quaternion,
• ${\vec {v}}\times {\vec {w}}$ is vector cross product (a vector),
• ${\vec {v}}\cdot {\vec {w}}$ is vector scalar product (a scalar).

Quaternion multiplication is noncommutative (because of the cross product, which anti-commutes), while scalar–scalar and scalar–vector multiplications commute. From these rules it follows immediately that (see details):

$(s+{\vec {v}})(t+{\vec {w}})=(st-{\vec {v}}\cdot {\vec {w}})+(s{\vec {w}}+t{\vec {v}}+{\vec {v}}\times {\vec {w}}).$

The (left and right) multiplicative inverse or reciprocal of a nonzero quaternion is given by the conjugate-to-norm ratio (see details):

$(s+{\vec {v}})^{-1}={\frac {(s+{\vec {v}})^{*}}{\lVert s+{\vec {v}}\rVert ^{2}}}={\frac {s-{\vec {v}}}{s^{2}+\lVert {\vec {v}}\rVert ^{2}}},$

as can be verified by direct calculation.

Proof of the quaternion rotation identity

Let ${\vec {u}}$ be a unit vector (the rotation axis) and let $q=\cos {\frac {\alpha }{2}}+{\vec {u}}\sin {\frac {\alpha }{2}}$. Our goal is to show that

${\vec {v'}}=q{\vec {v}}q^{-1}=\left(\cos {\frac {\alpha }{2}}+{\vec {u}}\sin {\frac {\alpha }{2}}\right)\,{\vec {v}}\,\left(\cos {\frac {\alpha }{2}}-{\vec {u}}\sin {\frac {\alpha }{2}}\right)$

yields the vector ${\vec {v}}$ rotated by an angle $\alpha$ around the axis ${\vec {u}}$. Expanding out, we have

${\begin{aligned}{\vec {v'}}&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+({\vec {u}}{\vec {v}}-{\vec {v}}{\vec {u}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-{\vec {u}}{\vec {v}}{\vec {u}}\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-({\vec {v}}({\vec {u}}\cdot {\vec {u}})-2{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}(\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}})+({\vec {u}}\times {\vec {v}})(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}})+{\vec {u}}({\vec {u}}\cdot {\vec {v}})(2\sin ^{2}{\frac {\alpha }{2}})\\[6pt]&={\vec {v}}\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})(1-\cos \alpha )\\[6pt]&=({\vec {v}}-{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})\\[6pt]&={\vec {v}}_{\bot }\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {v}}_{\|}\end{aligned}}$

where ${\vec {v}}_{\bot }$ and ${\vec {v}}_{\|}$ are the components of v→ perpendicular and parallel to u→ respectively. This is the formula of a rotation by α around the u→ axis.

Quaternion rotation operations

A very formal explanation of the properties used in this section is given by Altman.

The hypersphere of rotations

→詳細は「Rotation group SO(3)」を参照

Visualizing the space of rotations

Unit quaternions represent the group of Euclidean rotations in three dimensions in a very straightforward way. The correspondence between rotations and quaternions can be understood by first visualizing the space of rotations itself.

Two rotations by different angles and different axes in the space of rotations. The length of the vector is related to the magnitude of the rotation.

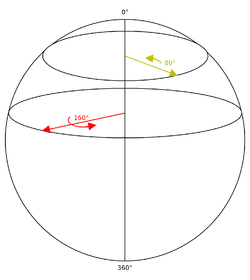
In order to visualize the space of rotations, it helps to consider a simpler case. Any rotation in three dimensions can be described by a rotation by some angle about some axis; for our purposes, we will use an axis vector to establish handedness for our angle. Consider the special case in which the axis of rotation lies in the xy plane. We can then specify the axis of one of these rotations by a point on a circle through which the vector crosses, and we can select the radius of the circle to denote the angle of rotation.

Similarly, a rotation whose axis of rotation lies in the xy plane can be described as a point on a sphere of fixed radius in three dimensions. Beginning at the north pole of a sphere in three-dimensional space, we specify the point at the north pole to be the identity rotation (a zero angle rotation). Just as in the case of the identity rotation, no axis of rotation is defined, and the angle of rotation (zero) is irrelevant. A rotation having a very small rotation angle can be specified by a slice through the sphere parallel to the xy plane and very near the north pole. The circle defined by this slice will be very small, corresponding to the small angle of the rotation. As the rotation angles become larger, the slice moves in the negative z direction, and the circles become larger until the equator of the sphere is reached, which will correspond to a rotation angle of 180 degrees. Continuing southward, the radii of the circles now become smaller (corresponding to the absolute value of the angle of the rotation considered as a negative number). Finally, as the south pole is reached, the circles shrink once more to the identity rotation, which is also specified as the point at the south pole.

Notice that a number of characteristics of such rotations and their representations can be seen by this visualization. The space of rotations is continuous, each rotation has a neighborhood of rotations which are nearly the same, and this neighborhood becomes flat as the neighborhood shrinks. Also, each rotation is actually represented by two antipodal points on the sphere, which are at opposite ends of a line through the center of the sphere. This reflects the fact that each rotation can be represented as a rotation about some axis, or, equivalently, as a negative rotation about an axis pointing in the opposite direction (a so-called double cover). The "latitude" of a circle representing a particular rotation angle will be half of the angle represented by that rotation, since as the point is moved from the north to south pole, the latitude ranges from zero to 180 degrees, while the angle of rotation ranges from 0 to 360 degrees. (the "longitude" of a point then represents a particular axis of rotation.) Note however that this set of rotations is not closed under composition. Two successive rotations with axes in the xy plane will not necessarily give a rotation whose axis lies in the xy plane, and thus cannot be represented as a point on the sphere. This will not be the case with a general rotation in 3-space, in which rotations do form a closed set under composition.

The sphere of rotations for the rotations that have a "horizontal" axis (in the xy plane).

This visualization can be extended to a general rotation in 3-dimensional space. The identity rotation is a point, and a small angle of rotation about some axis can be represented as a point on a sphere with a small radius. As the angle of rotation grows, the sphere grows, until the angle of rotation reaches 180 degrees, at which point the sphere begins to shrink, becoming a point as the angle approaches 360 degrees (or zero degrees from the negative direction). This set of expanding and contracting spheres represents a hypersphere in four dimensional space (a 3-sphere). Just as in the simpler example above, each rotation represented as a point on the hypersphere is matched by its antipodal point on that hypersphere. The "latitude" on the hypersphere will be half of the corresponding angle of rotation, and the neighborhood of any point will become "flatter" (i.e. be represented by a 3-D Euclidean space of points) as the neighborhood shrinks. This behavior is matched by the set of unit quaternions: A general quaternion represents a point in a four dimensional space, but constraining it to have unit magnitude yields a three-dimensional space equivalent to the surface of a hypersphere. The magnitude of the unit quaternion will be unity, corresponding to a hypersphere of unit radius. The vector part of a unit quaternion represents the radius of the 2-sphere corresponding to the axis of rotation, and its magnitude is the cosine of half the angle of rotation. Each rotation is represented by two unit quaternions of opposite sign, and, as in the space of rotations in three dimensions, the quaternion product of two unit quaternions will yield a unit quaternion. Also, the space of unit quaternions is "flat" in any infinitesimal neighborhood of a given unit quaternion.

Parameterizing the space of rotations

We can parameterize the surface of a sphere with two coordinates, such as latitude and longitude. But latitude and longitude are ill-behaved (degenerate) at the north and south poles, though the poles are not intrinsically different from any other points on the sphere. At the poles (latitudes +90° and −90°), the longitude becomes meaningless.

It can be shown that no two-parameter coordinate system can avoid such degeneracy. We can avoid such problems by embedding the sphere in three-dimensional space and parameterizing it with three Cartesian coordinates (w, x, y), placing the north pole at (w, x, y) = (1, 0, 0), the south pole at (w, x, y) = (−1, 0, 0), and the equator at w = 0, x² + y² = 1. Points on the sphere satisfy the constraint w² + x² + y² = 1, so we still have just two degrees of freedom though there are three coordinates. A point (w, x, y) on the sphere represents a rotation in the ordinary space around the horizontal axis directed by the vector (x, y, 0) by an angle $\alpha =2\cos ^{-1}w=2\sin ^{-1}{\sqrt {x^{2}+y^{2}}}$.

In the same way the hyperspherical space of 3D rotations can be parameterized by three angles (Euler angles), but any such parameterization is degenerate at some points on the hypersphere, leading to the problem of gimbal lock. We can avoid this by using four Euclidean coordinates w, x, y, z, with w² + x² + y² + z² = 1. The point (w, x, y, z) represents a rotation around the axis directed by the vector (x, y, z) by an angle $\alpha =2\cos ^{-1}w=2\sin ^{-1}{\sqrt {x^{2}+y^{2}+z^{2}}}.$

Explaining quaternions' properties with rotations

Non-commutativity

The multiplication of quaternions is non-commutative. This fact explains how the p ↦ q p q⁻¹ formula can work at all, having q q⁻¹ = 1 by definition. Since the multiplication of unit quaternions corresponds to the composition of three-dimensional rotations, this property can be made intuitive by showing that three-dimensional rotations are not commutative in general.

Set two books next to each other. Rotate one of them 90 degrees clockwise around the z axis, then flip it 180 degrees around the x axis. Take the other book, flip it 180° around x axis first, and 90° clockwise around z later. The two books do not end up parallel. This shows that, in general, the composition of two different rotations around two distinct spatial axes will not commute.

Orientation

The vector cross product, used to define the axis–angle representation, does confer an orientation ("handedness") to space: in a three-dimensional vector space, the three vectors in the equation a × b = c will always form a right-handed set (or a left-handed set, depending on how the cross product is defined), thus fixing an orientation in the vector space. Alternatively, the dependence on orientation is expressed in referring to such u→ that specifies a rotation as to axial vectors. In quaternionic formalism the choice of an orientation of the space corresponds to order of multiplication: ij = k but ji = −k. If one reverses the orientation, then the formula above becomes p ↦ q⁻¹ p q, i.e., a unit q is replaced with the conjugate quaternion – the same behaviour as of axial vectors.

Comparison with other representations of rotations

Advantages of quaternions

The representation of a rotation as a quaternion (4 numbers) is more compact than the representation as an orthogonal matrix (9 numbers). Furthermore, for a given axis and angle, one can easily construct the corresponding quaternion, and conversely, for a given quaternion one can easily read off the axis and the angle. Both of these are much harder with matrices or Euler angles.

In video games and other applications, one is often interested in “smooth rotations”, meaning that the scene should slowly rotate and not in a single step. This can be accomplished by choosing a curve such as the spherical linear interpolation in the quaternions, with one endpoint being the identity transformation 1 (or some other initial rotation) and the other being the intended final rotation. This is more problematic with other representations of rotations.

When composing several rotations on a computer, rounding errors necessarily accumulate. A quaternion that’s slightly off still represents a rotation after being normalised: a matrix that’s slightly off may not be orthogonal any more and is harder to convert back to a proper orthogonal matrix.

Quaternions also avoid a phenomenon called gimbal lock which can result when, for example in pitch/yaw/roll rotational systems, the pitch is rotated 90° up or down, so that yaw and roll then correspond to the same motion, and a degree of freedom of rotation is lost. In a gimbal-based aerospace inertial navigation system, for instance, this could have disastrous results if the aircraft is in a steep dive or ascent.

Conversion to and from the matrix representation

From a quaternion to an orthogonal matrix

The orthogonal matrix corresponding to a rotation by the unit quaternion z = a + b i + c j + d k (with | z | = 1) when post-multiplying with a column vector is given by

$R={\begin{pmatrix}a^{2}+b^{2}-c^{2}-d^{2}&2bc-2ad&2bd+2ac\\2bc+2ad&a^{2}-b^{2}+c^{2}-d^{2}&2cd-2ab\\2bd-2ac&2cd+2ab&a^{2}-b^{2}-c^{2}+d^{2}\\\end{pmatrix}}.$

This rotation matrix is used on vector w as $w_{rotated}=R\cdot w$. The quaternion representation of this rotation is given by:

${\begin{bmatrix}0\\w_{rotated}\end{bmatrix}}=z{\begin{bmatrix}0\\w\end{bmatrix}}z^{*},$

where $z^{*}$ is the conjugate of the quaternion $z$, given by $\mathbf {z} ^{*}=a-b\mathbf {i} -c\mathbf {j} -d\mathbf {k}$

Also, quaternion multiplication is defined as (assuming a and b are quaternions, like z above):

$ab=(a_{0}b_{0}-{\vec {a}}\cdot {\vec {b}};a_{0}{\vec {b}}+b_{0}{\vec {a}}+{\vec {a}}\times {\vec {b}})$

where the order a,b is important since the cross product of two vectors is not commutative.

From an orthogonal matrix to a quaternion

One must be careful when converting a rotation matrix to a quaternion, as several straightforward methods tend to be unstable when the trace (sum of the diagonal elements) of the rotation matrix is zero or very small. For a stable method of converting an orthogonal matrix to a quaternion, see the Quaternion subsection of the Rotation matrix article.

Fitting quaternions

The above section described how to recover a quaternion q from a 3×3 rotation matrix Q. Suppose, however, that we have some matrix Q that is not a pure rotation—due to round-off errors, for example—and we wish to find the quaternion q that most accurately represents Q. In that case we construct a symmetric 4×4 matrix

$K={\frac {1}{3}}{\begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_{xz}&Q_{yz}-Q_{zy}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{zx}-Q_{xz}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{xy}-Q_{yx}\\Q_{yz}-Q_{zy}&Q_{zx}-Q_{xz}&Q_{xy}-Q_{yx}&Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}},$

and find the eigenvector (x, y, z, w) corresponding to the largest eigenvalue (that value will be 1 if and only if Q is a pure rotation). The quaternion so obtained will correspond to the rotation closest to the original matrix Q

Performance comparisons

This section discusses the performance implications of using quaternions versus other methods (axis/angle or rotation matrices) to perform rotations in 3D.

Results

Storage requirements

Method	Storage
Rotation matrix	9
Quaternion	3 or 4 (see below)
Angle/axis	3 or 4 (see below)

Only three of the quaternion components are independent, as a rotation is represented by a unit quaternion. For further calculation one usually needs all four elements, so all calculations would suffer additional expense from recovering the fourth component. Likewise, angle/axis can be stored in a three-component vector by multiplying the unit direction by the angle (or a function thereof), but this comes at additional computational cost when using it for calculations.

Performance comparison of rotation chaining operations

Method	# multiplies	# add/subtracts	total operations
Rotation matrices	27	18	45
Quaternions	16	12	28

Performance comparison of vector rotating operations

Method	# multiplies	# add/subtracts	# sin/cos	total operations
Rotation matrix	9	6	0	15
Quaternions *	15	15	0	30
Angle/axis	18	12	2	30 + 2

* Note: Quaternions can be implicitly converted to a rotation-like matrix (12 multiplies and 12 add/subtracts), which levels the following vectors rotating cost with the rotation matrix method

Used methods

There are three basic approaches to rotating a vector v→:

1. Compute the matrix product of a 3 × 3 rotation matrix R and the original 3 × 1 column matrix representing v→. This requires 3 × (3 multiplications + 2 additions) = 9 multiplications and 6 additions, the most efficient method for rotating a vector.
2. A rotation can be represented by a unit-length quaternion q = (w, r→) with scalar (real) part w and vector (imaginary) part r→. The rotation can be applied to a 3D vector v→ via the formula ${\vec {v}}_{\text{new}}={\vec {v}}+2{\vec {r}}\times ({\vec {r}}\times {\vec {v}}+w{\vec {v}})$. This requires only 15 multiplications and 15 additions to evaluate (or 18 multiplications and 12 additions if the factor of 2 is done via multiplication.) This formula, originally thought to be used with axis/angle notation (Rodrigues' formula), can also be applied to quaternion notation. This yields the same result as the less efficient but more compact formula of quaternion multiplication ${\vec {v}}_{\text{new}}=q{\vec {v}}q^{-1}$.
3. Use the angle/axis formula to convert an angle/axis to a rotation matrix R then multiplying with a vector, or, similarly, use a formula to convert quaternion notation to a rotation matrix, then multiplying with a vector. Converting the angle/axis to R costs 12 multiplies, 2 function calls (sin, cos), and 10 add/subtracts; from item 1, rotating using R adds an additional 9 multiplications and 6 additions for a total of 21 multiplies, 16 add/subtracts, and 2 function calls (sin, cos). Converting a quaternion to R costs 12 multiplies and 12 add/subtracts; from item 1, rotating using R adds an additional 9 multiplications and 6 additions for a total of 21 multiplies and 18 add/subtracts.

Pairs of unit quaternions as rotations in 4D space

A pair of unit quaternions z_l and z_r can represent any rotation in 4D space. Given a four dimensional vector v→, and pretending that it is a quaternion, we can rotate the vector v→ like this:

$f({\vec {v}})=\mathbf {z} _{\rm {l}}{\vec {v}}\mathbf {z} _{\rm {r}}={\begin{pmatrix}a_{\rm {l}}&-b_{\rm {l}}&-c_{\rm {l}}&-d_{\rm {l}}\\b_{\rm {l}}&a_{\rm {l}}&-d_{\rm {l}}&c_{\rm {l}}\\c_{\rm {l}}&d_{\rm {l}}&a_{\rm {l}}&-b_{\rm {l}}\\d_{\rm {l}}&-c_{\rm {l}}&b_{\rm {l}}&a_{\rm {l}}\end{pmatrix}}{\begin{pmatrix}a_{\rm {r}}&-b_{\rm {r}}&-c_{\rm {r}}&-d_{\rm {r}}\\b_{\rm {r}}&a_{\rm {r}}&d_{\rm {r}}&-c_{\rm {r}}\\c_{\rm {r}}&-d_{\rm {r}}&a_{\rm {r}}&b_{\rm {r}}\\d_{\rm {r}}&c_{\rm {r}}&-b_{\rm {r}}&a_{\rm {r}}\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}.$

The pair of matrices represents a rotation of ℝ⁴. Note that since $(\mathbf {z} _{\rm {l}}{\vec {v}})\mathbf {z} _{\rm {r}}=\mathbf {z} _{\rm {l}}({\vec {v}}\mathbf {z} _{\rm {r}})$, the two matrices must commute. Therefore, there are two commuting subgroups of the set of four dimensional rotations. Arbitrary four dimensional rotations have 6 degrees of freedom, each matrix represents 3 of those 6 degrees of freedom.

Since the generators of the four-dimensional rotations can be represented by pairs of quaternions (as follows), all four-dimensional rotations can also be represented.

$\mathbf {z} _{\rm {l}}{\vec {v}}\mathbf {z} _{\rm {r}}={\begin{pmatrix}1&-dt_{ab}&-dt_{ac}&-dt_{ad}\\dt_{ab}&1&-dt_{bc}&-dt_{bd}\\dt_{ac}&dt_{bc}&1&-dt_{cd}\\dt_{ad}&dt_{bd}&dt_{cd}&1\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}$

$\mathbf {z} _{\rm {l}}=1+{dt_{ab}+dt_{cd} \over 2}i+{dt_{ac}-dt_{bd} \over 2}j+{dt_{ad}+dt_{bc} \over 2}k$

$\mathbf {z} _{\rm {r}}=1+{dt_{ab}-dt_{cd} \over 2}i+{dt_{ac}+dt_{bd} \over 2}j+{dt_{ad}-dt_{bc} \over 2}k$

See also

• Anti-twister mechanism
• Binary polyhedral group
• Biquaternion
• Charts on SO(3)
• Clifford algebras
• Conversion between quaternions and Euler angles
• Covering space
• Dual quaternion
• Elliptic geometry
• Rotation formalisms in three dimensions
• Rotation (mathematics)
• Spin group
• Slerp, spherical linear interpolation
• Olinde Rodrigues
• William Rowan Hamilton

References

• Grubin, Carl (1970年). “Derivation of the quaternion scheme via the Euler axis and angle”. J. Spacecraft Rockets 7 (10): pp. 1261–1263. Bibcode: 1970JSpRo...7.1261G. doi:10.2514/3.30149 
• Battey-Pratt, E. P.; Racey, T. J. (1980年). “Geometric Model for Fundamental Particles”. International Journal of Theoretical Physics 19 (6). Bibcode: 1980IJTP...19..437B. doi:10.1007/BF00671608 

• Arribas, M.; Elipe, A.; Palacios, M. (2006). “Quaternions and the rotations of a rigid body”. Celestial Mech. Dyn. Astr. 96: 239–251. Bibcode: 2006CeMDA..96..239A. doi:10.1007/s10569-006-9037-6. 

External links and resources

• “Quaternions”.
• “Simple Quaternion type and operations in over thirty computer languages”. on Rosetta Code
• “Quaternion Demonstrator”.
• “Quaternions, Interpolation and Animation” (1998年).
• “Quaternions and Rotations in 3-Space: The Algebra and its Geometric Interpretation” (2001年).
• “The Complexity of the Quaternion Product, TR75-245”. Cornell University (1975年).
• “Some Notes on Unit Quaternions and Rotation” (2001年).
• Lee, Byung-Uk (1991). Unit Quaternion Representation of Rotation - Appendix A, Differentiation with Quaternions - Appendix B (PDF) (Ph. D. Thesis). Stanford University.
• “Some examples of connected Lie groups”.

3次元空間では、オイラーの回転定理によれば、固定点を中心とした剛体または座標系の任意の回転または回転シーケンスは、固定軸（オイラー軸と呼ばれる）の周りの所与の角度θによる単一の回転に相当し、固定小数点を介して実行されます。オイラー軸は、通常、単位ベクトルu →で表されます。したがって、三次元における任意の回転は、ベクトルu → およびスカラーθの組み合わせとして表すことができる 。クォータニオンは、この軸角度表現を4つの数字でエンコードする簡単な方法を提供し、対応するローテーションを 位置ベクトルを表す、点に対して原点におけるR 3。

空間ベクトルのような（2、3、4）又は（X、  Y、  Zが）のように書き換えることができる2  iが + 3  J + 4  KまたはX iは + Yの J + Zの kは、I、j、kは、3つのデカルト軸を表す単位ベクトルである。単位ベクトルによって定義される軸の周りの 角度θを通る回転   

u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ { z} \ mathbf {k}} {\ vec {u}} =（u_ {x}、u_ {y}、u_ {z}）= u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ {z} \ mathbf {k} 四元数で表すことができる。これは、オイラーの公式の拡張を使用して行うことができます：

{u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ {z} \ {\ displaystyle \ mathbf {q} = e ^ {\ frac {\ theta} mathbf {j} \ mathbf {j} \ mathbf {j} \ u {z} \ mathbf { k}）\ sin {\ frac {\ theta} {2}}} \ mathbf {q} = e ^ {{\ frac {\ theta} {2}} {（u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ {z} \ mathbf {k }）}} = \ cos {\ frac {\ theta} {2}} +（u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ {z} \ mathbf {k}） \ sin {\ frac {\ theta} {2}} 所望の回転を通常のベクトルに適用することができることを示すことができる mathbf {j} + p_ {z}）= p_ {x} \ mathbf {i} + p_ {y} \ mathbf {p} {p} \ mathbf {k}} \ mathbf {p} = p_ {x}、p_ {z}）= p_ {x} \ mathbf {i} + p_ {y} \ mathbf { k} 3次元空間において、実際のと四元数として考え評価することによって、ゼロに等しい座標コンジュゲーションの Pをすることによって Q：

{\ displaystyle \ mathbf {p}} \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ { - 1}} \ mathbf {p} = \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {-1} 使用ハミルトン製品、P '=（PのX '、  PのY '、  p個のZは '）回転後の点の新しい位置ベクトルです。プログラムによる実装では、これはベクトル部分がpで実数部分がゼロに等しい四元数を構築し、次に四元数乗算を実行することで実現されます。結果として生じる四元数のベクトル部分は、所望のベクトルp 'である。

数学的には、この演算は、四元数の中の三次元空間を構成するすべての「純粋な」四元数p（実数部がゼロに等しいもの）のセットを、軸uを中心とする所望の回転角度θ。（それぞれの実際の四元数はこの操作で持ち込まれますが、三次元空間での回転の目的では、実際の四元数は無視されます）。

私たちの視線がu →と同じ方向を向いている場合、回転は時計回りです。

この場合、qは単位四元数であり、

{u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} {\ displaystyle \ mathbf {q} ^ { - 1} = e ^ u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ { {z} \ mathbf {k}）\ sin {\ frac {\ theta} {2}}} \ mathbf {q} ^ {-1} = e ^ { - {\ frac {\ theta} {2}} {（u_ {x} \ mathbf { z} \ mathbf {k}）}}}} = \ cos {\ frac {\ theta} {2}} - （u_ {x} \ mathbf {i} + u_ {y} \ mathbf { \ mathbf {k}）\ sin {\ frac {\ theta} {2}}となります。 2つの四元数の積による共役は、これらの四元数による共役の構成である：pとqが単位四元数である場合、pqによる回転（共役） は次のようになる。

^ { - 1} = \ mathbf {pq} {\ vec {v}} \ mathbf {q} ^ { - 1} {\ displaystyle \ mathbf {pq} {\ vec { \ mathbf {p} ^ { - 1} \ mathbf {p} ^ { - 1} = \ mathbf { } \ mathbf {p}} \ {\ vec {v}} \ mathbf {p} {\ vec {v}} \ mathbf { \ mathbf {q} {\ vec {v}} \ mathbf {q} ^ { - 1}）\ mathbf {p} ^ { - 1}、 これはqで回転し（共役）、次に pで回転することと同じ です。結果のスカラー成分は必然的にゼロです。

回転の四元数の逆数は反対の回転です。 \ mathbf {q} {\ vec {v}} \ mathbf {q} ^ { - 1}）{\ displaystyle \ mathbf { } \ mathbf {q} ^ { - 1}（\ mathbf {q} {\ vec {v}} \ mathbf {q} ^ {-1}）\ mathbf {q} = {\ vec {v}}。クォータニオン回転の2乗は、同じ軸を中心とした2倍の回転です。より一般的には、q個のnがによって回転で Nと同じ軸周り回角度Q。これは任意の実数nに拡張することができ、空間的な向きの間の滑らかな補間を可能にする。Slerpを参照してください。

2つの回転四元数は、次の関係によって1つの等価四元数に結合できます。

{\ displaystyle \ mathbf {q} '= \ mathbf {q} _ {2} \ mathbf {q} _ {1}} \ mathbf {q} '= \ mathbf {q} _ {2} \ mathbf {q} _ {1} ここでq 'は回転q 1に続いて回転q 2に対応する。（四元数乗法は可換ではないことに注意してください。）したがって、任意の数の回転を一緒に構成してから、1回の回転として適用することができます。

例 共役操作

第1の対角の周りの120°の回転は、周期的にi、j、およびkを置換する。 共役 Pを することによって 、Qする操作を意味するP ↦ Q PがQ -1。

軸周りの回転fを考える \ {\ displaystyle {\ vec {v}} = \ mathbf {i} + \ mathbf {j} + \ mathbf {k}} {\ vec {v}} = \ mathbf {i} + \ mathbf {j} + \ mathbf {k} 120°、または 2π / 3

ラジアンの回転角を有する。

{\ displaystyle \ alpha = {\ dfrac {2 \ pi} {3}}} {\ displaystyle \ alpha = {\ dfrac {2 \ pi} {3}}}

ユニット 3球面上のq = 1 + i + j + k / 2 に対して p≥q pである。この片側（すなわち、左）乗算は、クォータニオンの60°回転をもたらすことに注意してください 長さのV →がある√ 3半分の角度は、 π / 3 を有する（60°）余弦 1 / 2 、（60°= 0.5 COS及び）正弦 √ 3 / 2 、（罪60°≈0.866）。それゆえ、我々は単位四元数による共役を扱っている

{\ displaystyle {\ begin {array} {lll} u＆=＆\ cos {\ dfrac {\ alpha} {2}} + \ sin {\ dfrac {\ alpha} {2}} \ cdot { {\ | {\ vec {v}} \ |}} {\ vec {v}} \\＆=＆\ cos {\ dfrac {\ pi} {3}} + \ sin {\ dfrac {\ pi} { 3}} \ cdot {\ dfrac {1} {\ sqrt {3}}} {\ vec {v}} \\＆=＆{\ dfrac {1} {2}} + {\ dfrac {\ sqrt {3 }} {2}} {\ dfrac {1} {\ sqrt {3}}} {\ vec {v}} \\＆=＆{\ dfrac {1} {2}} + sqrt {3}} {2}} \ cdot {\ dfrac {\ mathbf {i} + \ mathbf {j} + \ mathbf {\ sqrt {3}}} \\＆=＆{\ dfrac { 1 + \ mathbf {i} + \ mathbf {j} + \ mathbf {k}} {2}} \ end {配列}}} {\ displaystyle {\ begin {array} {lll} u＆=＆\ cos {\ dfrac {\ alpha} {2}} + \ sin {\ dfrac {\ alpha} {2}} \ cdot { {\ | {\ vec {v}} \ |}} {\ vec {v}} \\＆=＆\ cos {\ dfrac {\ pi} {3}} + \ sin {\ dfrac {\ pi} { 3}} \ cdot {\ dfrac {1} {\ sqrt {3}}} {\ vec {v}} \\＆=＆{\ dfrac {1} {2}} + {\ dfrac {\ sqrt {3 }} {2}} {\ dfrac {1} {\ sqrt {3}}} {\ vec {v}} \\＆=＆{\ dfrac {1} {2}} + sqrt {3}} {2}} \ cdot {\ dfrac {\ mathbf {i} + \ mathbf {j} + \ mathbf {\ sqrt {3}}} \\＆=＆{\ dfrac { 1 + \ mathbf {i} + \ mathbf {j} + \ mathbf {k}} {2}} \ end {配列}}} もしfが回転機能です、

\（a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k}）= u u ^ { - 1}} f（a \ mathbf {i} + b \ mathbf {k}）= u（a \ mathbf {i} + b \ mathbf {j} + c \ mathbf { -1} 単位四元数の逆数は、その虚数成分の符号を変えるだけで得られることが証明されます。結果として、

{\ displaystyle u ^ { - 1} = {\ dfrac {1- \ mathbf {i} - \ mathbf {j} - \ mathbf {k}} {2}}} {\ displaystyle u ^ { - 1} = {\ dfrac {1- \ mathbf {i} - \ mathbf {j} - \ mathbf {k}} {2}}} そして

{\ displaystyle f（a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k}）= {\ dfrac {1+ \ mathbf {i} + \ mathbf {j} + \ mathbf { mathbf {k}）{\ mathbf {i} - \ mathbf {j} - \ mathbf {k} } {2}}} {\ displaystyle f（a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k}）= {\ dfrac {1+ \ mathbf {i} + \ mathbf {j} + \ mathbf { mathbf {k}）{\ mathbf {i} - \ mathbf {j} - \ mathbf {k} } {2}}} これは、四元数演算の通常の規則を使用して、

\ mathbf {i} + b \ mathbf {k}} = c \ mathbf {i} + a \ mathbf {j} + b \ mathbf {k}} f（a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k}）= c \ mathbf {i} + a \ mathbf {j} + b \ mathbf {k} 予想されるように、回転は1つの点に固定された立方体を保持し、固定点を通って長い対角線の周りに120°回転させることに対応する（3つの軸が周期的にどのように置換されるかを観察する）。

クォータニオン派生回転行列 四元数回転 {\ displaystyle \ mathbf {p}} \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ { - 1}} \ mathbf {p} = \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {-1} （with mathbf {q} = q_ {r} + q_ {i} \ mathbf {i} + q_ {j} \ mathbf {j} + q_ {k} \ mathbf {k}} mathbf {q} = q_ {r} + q_ {i} \ mathbf {i} + q_ {j} \ mathbf {j} + q_ {k} \ mathbf {k}}）は行列の回転に代数的に操作できます {\ displaystyle \ mathbf {p '} = \ mathbf {Rp}} {\ displaystyle \ mathbf {p '} = \ mathbf {Rp}}ここで、Rは[6]で与えられる回転行列です。

{2}（q_ {j} ^ {2} + q_ {k} ^ {2}）＆2s（q_ {i} q_ {j} + q_ {k}、q_ {j}、q_ {q}、q_ { } 2（q_ {j} q_ {k} -q_ {i} q_ {r}） 2s（q_ {j} q_ {k} + q_ {i} q_ {r}）＆2s（q_ { 2} + q_ {j} ^ {2}）\ end {bmatrix}} \ end {aligned}}} {2}（q_ {j} ^ {2} + q_ {k} ^ {2}）＆2s（q_ {i} q_ {j} + q_ {k}、q_ {j}、q_ {q}、q_ { } 2（q_ {j} q_ {k} -q_ {i} q_ {r}） 2s（q_ {j} q_ {k} + q_ {i} q_ {r}）＆2s（q_ { 2} + q_ {j} ^ {2}）\ end {bmatrix}} \ end {aligned}}} ここに {\ displaystyle s = || q || ^ { - 2}} {\ displaystyle s = || q || ^ { - 2}}qが単位四元数である場合、 {\ displaystyle s = 1} s = 1

これは、ベクトル微積分と線形代数を使用して表現することができます {\ displaystyle \ mathbf {p}} \ mathbf {p} そして {\ displaystyle \ mathbf {q}} \ mathbf qスカラーおよびベクトル部分として、式の乗算演算の式を使用します {\ displaystyle \ mathbf {p}} \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ { - 1}} \ mathbf {p} = \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {-1}。私たちが書くなら {\ displaystyle \ mathbf {p}} \ mathbf {p} として {\ displaystyle（0、\ \ mathbf {p}）} {\ displaystyle（0、\ \ mathbf {p}）}、 {\ displaystyle \ mathbf {p} '} {\ displaystyle \ mathbf {p} '} として {\ displaystyle（0、\ \ mathbf {p} '}} {\ displaystyle（0、\ \ mathbf {p} '}} そして {\ displaystyle \ mathbf {q}} \ mathbf q として {\ displaystyle（q_ {r}、\ \ mathbf {v}）} {\ displaystyle（q_ {r}、\ \ mathbf {v}）}、どこで {\ displaystyle \ mathbf {v} =（q_ {i}、q_ {j}、q_ {k}}} {\ displaystyle \ mathbf {v} =（q_ {i}、q_ {j}、q_ {k}}}、私たちの方程式は （0、\ \ mathbf {p}）=（q_ {r}、\ \ mathbf { v}）} （0、\ \ mathbf {p}）=（q_ {r}、\ \ mathbf { v}）}。スカラーおよびベクトル部分として表現される2つの四元数の乗算の式を使用することによって、

\ {\ displaystyle（r_ {1}、\ {\ vec {v}} _ {1}）（r_ {2}、\ {\ vec {v}} _ {2}）= }} {\ vec {v}} _ {2} + r_ {2} {\ vec { vec {v}} _ {1} + {\ vec {v}} _ {1} \ times {\ vec {v}} _ {2}）、} \ {\ displaystyle（r_ {1}、\ {\ vec {v}} _ {1}）（r_ {2}、\ {\ vec {v}} _ {2}）= }} {\ vec {v}} _ {2} + r_ {2} {\ vec { vec {v}} _ {1} + {\ vec {v}} _ {1} \ times {\ vec {v}} _ {2}）、} この方程式は次のように書き換えることができます

{\displaystyle {\begin{aligned}(0,\ \mathbf {p} ')=&\ ((q_{r},\ \mathbf {v} )(0,\ \mathbf {p} ))s(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ (q_{r}\times 0-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +0\mathbf {v} +\mathbf {v} \times \mathbf {p} )s(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} q_{r}-(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\cdot (-\mathbf {v} ),\ (-\mathbf {v} \cdot \mathbf {p} )(-\mathbf {v} )+q_{r}(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )+(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\times (-\mathbf {v} ))\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} q_{r}+q_{r}\mathbf {v} \cdot \mathbf {p} ,\ \mathbf {v} (\mathbf {v} \cdot \mathbf {p} )+q_{r}^{2}\mathbf {p} +q_{r}\mathbf {v} \times \mathbf {p} +\mathbf {v} \times (q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} ))\\(0,\ \mathbf {p} ')=&\ (0,\ s(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2})\mathbf {p} ),\end{aligned}}} （0、\ \ mathbf {p}））（s、（\）、\ \ mathbf { \ cdath \ mathbf {p} \ \ mathbf {v}）\\（0、\ \ mathbf {p}）=＆\（q_ {r} mathbf {v} \ \ mathbf {v} \ times \ mathbf {p}）\（\ r \ mathbf { 0、\ \ mathbf {p} '）= \ \ s（ - \ mathbf {v} \ cdot \ mathbf {p}、\ q_ {r} \ mathbf { p}} \ {\ mathbf {p}} \ {\ mathbf {p}} \ （\ mathbf {v}）、\ cdot \ mathbf（\ mathbf {\}、\ mathbf { {p}）+（q_ {r} \ mathbf {p} + \ mathbf { \\（0、\ \ mathbf {p} '）=＆\ mathbf {p}）\ times（mathbf {\ mathbf {v} \ mathbf {v} \ cdath \ mathbf {v} \ cdath \ mathbf { \ cdot \ mathbf {p}）+ q_ {r} ^ {2} \ mathbf {p} + q_ {r} \ mathbf {v} \ times \ mathbf {p} + \ mathbf {v} \ times （0、\ \ mathbf {p} '）=＆\（0、\ s（\ mathbf {v} \）\ mathbf { {\ mathbf {v}] _ {\ times} {\ mathbf {v}} \ {\ times} ^ {2}）\ mathbf {p}）、\ end {aligned}}} どこで {\ displaystyle \ otimes} \ otimes 外積を示し、 {\ displaystyle \ mathbf {I}} \ mathbf {I} ある単位行列をと {\ displaystyle [\ mathbf {v}] _ {\ times}} {\ displaystyle [\ mathbf {v}] _ {\ times}} は左からベクトルで掛け合わされたときの変換行列です {\ displaystyle \ mathbf {u}} \ mathbf uクロスプロダクトを与える {\ displaystyle \ mathbf {v} \ times \ mathbf {u}} {\ displaystyle \ mathbf {v} \ times \ mathbf {u}}。

以来 {\ displaystyle \ mathbf {p} '= \ mathbf {R} \ mathbf {p}} {\ displaystyle \ mathbf {p} '= \ mathbf {R} \ mathbf {p}}、我々は {\ displaystyle \ mathbf {R}} \ mathbf {R} として {\} {\ mathbf {v} \ {\ times} + [{\ mathbf { \ mathbf {v}] _ {\ times} ^ {2}}} {\} {\ mathbf {v} \ {\ times} + [{\ mathbf { \ mathbf {v}] _ {\ times} ^ {2}}}展開時に上記の行列形式で表現されるべきである。

軸の角度表示の復元 表現 {\ displaystyle \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ { - 1}} {\ displaystyle \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ { - 1}}任意のベクトル四元数を回転する {\ displaystyle \ mathbf {p}} \ mathbf {p} ベクトルによって与えられた軸の周り {\ displaystyle \ mathbf {a}} \ mathbf {a} 角で {\ displaystyle \ theta} \ theta 、どこで {\ displaystyle \ mathbf {a}} \ mathbf {a} そして {\ displaystyle \ theta} \ theta 四元数に依存する mathbf {q} = q_ {r} + q_ {i} \ mathbf {i} + q_ {j} \ mathbf {j} + q_ {k} \ mathbf {k}} mathbf {q} = q_ {r} + q_ {i} \ mathbf {i} + q_ {j} \ mathbf {j} + q_ {k} \ mathbf {k}}。

{\ displaystyle \ mathbf {a}} \ mathbf {a} そして {\ displaystyle \ theta} \ theta 次の式から求めることができます。

{\ displaystyle（a_ {x}、a_ {y}、a_ {z}）\ = \ {\ frac {（q_ {i}、q_ {j}、q_ {k}}} {\ sqrt {q_ {i } ^ {2} + q_ {j} ^ {2} + q_ {k} ^ {2}}}}} {\ displaystyle（a_ {x}、a_ {y}、a_ {z}）\ = \ {\ frac {（q_ {i}、q_ {j}、q_ {k}}} {\ sqrt {q_ {i } ^ {2} + q_ {j} ^ {2} + q_ {k} ^ {2}}}}} {\ displaystyle \ theta \ = \ 2 \ operatorname {atan2} \ left（{\ sqrt {q_ {i} ^ {2} + q_ {j} ^ {2} + q_ {k} ^ {2}}} q_ {r} \ right）、} {\ displaystyle \ theta \ = \ 2 \ operatorname {atan2} \ left（{\ sqrt {q_ {i} ^ {2} + q_ {j} ^ {2} + q_ {k} ^ {2}}} q_ {r} \ right）、} どこで {\ displaystyle \ mathrm {atan2}} {\ displaystyle \ mathrm {atan2}}ある2つの引数のアークタンジェントは。縮退のために、身元回旋の軸は明確に定義されていないので、四元数がスカラーに近づくときには注意が必要です。

空間回転の構成 2つの回転R BおよびR Aの組成の四元数の定式化の利点は、それが複合回転R C = R B R Aの回転軸および角度を直接もたらすことである。

空間回転Rに関連する四元数をその回転軸 Sとこの軸の回転角φとから構築する。関連する四元数は、

S = \ cos {\ frac {\ phi} {2}} + \ sin {\ frac {\ phi} {2}} \ mathbf {S}} S = \ cos {\ frac {\ phi} {2}} + \ sin {\ frac {\ phi} {2}} \ mathbf {S}} 次に、R Aを有する回転R Rの構成は、回転軸および角度が四元数の積によって定義される回転R C = R B R Aである

\ {\ displaystyle A \ \ cos {\ alpha {2}} + \ sin {\ frac {\ alpha} {2}} \ mathbf {A} \ quad {\ text {and}} \ quad B = \ cos {\ frac {\ beta} {2}} + \ sin {\ frac {\ beta} {2}} \ mathbf {B}、} \ {\ displaystyle A \ \ cos {\ alpha {2}} + \ sin {\ frac {\ alpha} {2}} \ mathbf {A} \ quad {\ text {and}} \ quad B = \ cos {\ frac {\ beta} {2}} + \ sin {\ frac {\ beta} {2}} \ mathbf {B}、} あれは

\ mathbf {C} = {\ Big（} \ cos {\ frac {\ frac {\ gamma} {\ frac {\ gamma} {\ frac {\ alpha} {2}} + \ bash {2}} + \ sin {\ frac {\ beta} {2}} \ mathbf { sin {\ frac {\ alpha} {2}} \ mathbf {A} {\ Big}}} \ mathbf {C} = {\ Big（} \ cos {\ frac {\ frac {\ gamma} {\ frac {\ gamma} {\ frac {\ alpha} {2}} + \ bash {2}} + \ sin {\ frac {\ beta} {2}} \ mathbf { sin {\ frac {\ alpha} {2}} \ mathbf {A} {\ Big}}} 入手するにはこの製品を展開してください

\ {\ displaystyle \ cos {\ frac {\ gamma} {2}} + \ sin {\ frac {\ gamma} {2}} \ mathbf {C} = {\ Big {} \ cos {\ frac {\ beta} {2}} \ mathbf {B} \ {sin {\ frac {\ alpha} {2}} \ \ mathbf {B} + \ fB {\ frac {\ alpha} {2}} \ cdath \ mathbf { sin {\ frac {\ alpha} {2}} \ cos {\ frac {\ beta} {2}} \ mathbf {A} + \ sin {\ frac {\ beta} {2}} \ sin {\ frac { \ alpha} {2}} \ mathbf {B} \ times \ mathbf {A} {\ Big}}} \ {\ displaystyle \ cos {\ frac {\ gamma} {2}} + \ sin {\ frac {\ gamma} {2}} \ mathbf {C} = {\ Big {} \ cos {\ frac {\ beta} {2}} \ mathbf {B} \ {sin {\ frac {\ alpha} {2}} \ \ mathbf {B} + \ fB {\ frac {\ alpha} {2}} \ cdath \ mathbf { sin {\ frac {\ alpha} {2}} \ cos {\ frac {\ beta} {2}} \ mathbf {A} + \ sin {\ frac {\ beta} {2}} \ sin {\ frac { \ alpha} {2}} \ mathbf {B} \ times \ mathbf {A} {\ Big}}} 球面上の余弦の法則であるアイデンティティによってこの方程式の両辺を分け、

{\ frac {\ gamma} {2}} = \ cos {\ frac {\ beta} {2}} \ cos {\ frac {\ alpha} {2}} - \ beta {2}} \ sin {\ frac {\ alpha} {2}} \ mathbf {B} \ cdot \ mathbf {A}、} {\ frac {\ gamma} {2}} = \ cos {\ frac {\ beta} {2}} \ cos {\ frac {\ alpha} {2}} - \ beta {2}} \ sin {\ frac {\ alpha} {2}} \ mathbf {B} \ cdot \ mathbf {A}、} 計算する

{\ frac {\ frac {\ gamma} {2}} \ mathbf {C} = {\ frac {\ frac {\ frac {\ beta} {2}} \ mathbf {B} + \ tan {\ frac {\ alpha} {2}} \ mathbf {B} \ times \ mathbf {\ alpha} {2}} \ mathbf { 2}} \ mathbf {B} \ cdot \ mathbf {A}}}。}} {} {} {\ frac {\ frac {\ gamma} {2}} \ mathbf {C} = {\ frac {\ frac {\ frac {\ beta} {2}} \ mathbf {B} + \ tan {\ frac {\ alpha} {2}} \ mathbf {B} \ times \ mathbf {\ alpha} {2}} \ mathbf { 2}} \ mathbf {B} \ cdot \ mathbf {A}}}。}} {} {} これは、2つの回転の軸に関して定義された複合回転軸のロドリゲス公式です。彼は1840年にこの式を導き出しました（408ページ参照）。[7]

3つの回転軸A、B、Cは球面三角形を形成し、この三角形の辺によって形成される面間の二面角は回転角によって定義される。Hamilton [8]は、これらの方程式のコンポーネント形式を提示し、四元数積が2つの与えられた頂点からの球面三角形の3番目の頂点とそれに関連する弧長を計算し、楕円幾何学における点の代数も定義することを示した。

回転四元数の微分 数値的な最適化から回転を推定するとき、回転した四元数q に対して、回転四元数p '= q p q *を微分する必要がある。回転角の推定は、3Dオブジェクトの登録またはカメラ較正に不可欠な手順です。デリバティブは、マトリックス微積分表記を使用して表すことができます 。

\ equiv \ left [{\ frac {\ partial \ mathbf {p '}} {\ frac {\ partial {mathbf {p}} \ {\ frac {\ frac {\ partial} \ mathbf {p}} {\ partial q_ {0}}} \ right {\ mathbf {pq} - {\ mathbf {pq}）^ {left} （\ mathbf {pqk}）^ {*}、\ mathbf {pqi}、\ mathbf {pqi} - \ mathbf {pqk} \ right]。\ end {aligned}}} \ equiv \ left [{\ frac {\ partial \ mathbf {p '}} {\ frac {\ partial {mathbf {p}} \ {\ frac {\ frac {\ partial} \ mathbf {p}} {\ partial q_ {0}}} \ right {\ mathbf {pq} - {\ mathbf {pq}）^ {left} （\ mathbf {pqk}）^ {*}、\ mathbf {pqi}、\ mathbf {pqi} - \ mathbf {pqk} \ right]。\ end {aligned}}} 導出は[9]で見つけることができます。

はじめに 四元数 主な記事：四元数 複素数は、抽象記号導入することによって定義することができるI代数の通常の規則、さらにルール満たし、I 2 = -1。これは、複素数演算のすべての規則を再現するのに十分です。たとえば、次のようになります。

{\ displaystyle（a + b \ mathbf {i}）= ac + ad \ mathbf {i} + b \ mathbf {i} c + b \ mathbf {i} d \ mathbf {2} =（ac-bd）+（bc + ad）\ mathbf {i}。{i} = ac + ad \ mathbf {i} + bc \ mathbf {i} + bd \ mathbf { （a + b \ mathbf {i}）= ac + ad \ mathbf {i} + b \ mathbf {i} c + b \ mathbf {i} d \ mathbf {i} =（ac-bd）+（bc + ad）\ mathbf {i}となる。 同様に四元数は、抽象記号を導入することによって定義することができ、I、J、Kルールを満たす、I 2 = J 2 = K 2 = I jのkの = -1、通常の代数的ルール以外乗算の交換法則（身近な例このような非可換倍は行列積である）。このことから、四元数の基本的な要素の乗算に関する規則のような四元数の算術規則のすべてが従う。これらのルールを使用すると、次のことが分かります。

\ mathbf {k}）（e + f \ mathbf {i} + g \ mathbf {j} + h \ mathbf {k} ）=} （a + b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k}）（e + f \ mathbf {i} + g \ mathbf {j} + h \ mathbf { \ mathbf {i} +（ag-bh + ce + df）\ mathbf {j} +（ah + bg-cf + dg） de）\ mathbf {k}。} （ah + bg-cf + de）\（ae-bf-cg-dh）+（af + be + ch-dg）\ mathbf {i} +（ag-bh + ce + df）\ mathbf { mathbf {k}。

虚数部 {\ displaystyle b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k}} b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k} 四元数のベクトルがベクトルのように振舞う {\ displaystyle {\ vec {v}} =（b、c、d）} {\ vec {v}} =（b、c、d）3次元のベクトル空間、および実部におけるように振る舞うスカラーでR。四元数がジオメトリで使用される場合、それらをスカラーとベクトルに定義する方が便利です。

{\ displaystyle a + b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k} = a + {\ vec {v}}。} a + b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k} = a + {\ vec {v}}である。 学校でベクトルを勉強した人は、非常に異なる性質のオブジェクトであるため、ベクトルに数値を加えることや、通常は定義されていないので、2つのベクトルを掛けることは奇妙です。しかし、四元数の実数部と虚数部の単なる表記であることを覚えていれば、それはより合法的になります。換言すれば、正当な推論は、ゼロベクトル/虚数部を有するものとスカラー/実数部がゼロのものとの2つの四元数の加算である。

{\ vec {v}}）=（a、{\ vec {0}}）+（0、{\ vec {v}}）}} a + {\ vec {v}} =（a、{\ vec {0}}）+（0、{\ vec {v}}）。 我々はベクトルクロスとドットプロダクトの現代語で四元数の乗法を表現することができます（実際には四元数に最初に触発されました[10]）。ベクトル/虚数部を掛けるとき、ルールi 2 = j 2 = k 2 = ijk = -1の代わりに、四元数の乗算ルールがあります。

\ times {\ vec {w ve} {\ vec {w}} \ {vec {w ve} {\ vec { }、} {\ vec {w}} \ {vec {w ve} {\ vec {w}} \ {vec {w ve} ここで：

{\ displaystyle {\ vec {v}} {\ vec {w}}} {\ vec {v}} {\ vec {w}} 結果として生じる四元数であり、 {\ displaystyle {\ vec {v}} \ times {\ vec {w}}} {\ vec {v}} \ times {\ vec {w}} ベクトル交差積（ベクトル）です。 {\ displaystyle {\ vec {v}} \ cdot {\ vec {w}}} {\ vec {v}} \ cdot {\ vec {w}} ベクトルスカラ積（スカラー）です。 クォータニオン乗算は（スカラスカラーとスカラーベクトル乗算が通勤している間、反通勤のクロス積のために）非可換です。これらの規則から、すぐにそれが続きます（詳細を参照）。

（st + {vec {w}}）+（s {\ vec {v ve}}） {w}} + t {\ vec {v}} + {\ vec {v}} \ times {\ vec {w}}）} （t + {vec {w ve}））=（st - {\ vec {v}} \ cdot {\ vec {w}}）+（s {vec {w}}） } + t {\ vec {v}} + {\ vec {v}} \ times {\ vec {w}}）。 非ゼロクォータニオンの（左と右の）乗法逆数または逆数は、共役対ノルム比によって与えられる（詳細を参照）。

{\ displaystyle（s + {\ vec {v}}）^ { - 1} = {\ frac {（s + {\ vec {v}}） rVert ^ {2}}} = {\ frac {s - {\ vec {v}}} {s ^ {2} + \ lVert {\ vec {v}} \ rVert ^ {2}}}、} （s + {\ vec {v}}）^ { - 1} = {\ frac {（s + {\ vec {v}}） {2}}}} {} {}}}} {} {}}}} {} {}} 直接計算によって検証することができる。

四元数回転識別の証明 レッツ {\ displaystyle {\ vec {u}}} {\ vec {u}} 単位ベクトル（回転軸）とし、 {\ displaystyle q = \ cos {\ frac {\ alpha} {2}} + {\ vec {u}} \ sin {\ alpha {2}}} q = \ cos {\ frac {\ alpha} {2}} + {\ vec {u}} \ sin {\ frac {\ alpha} {2}}。私たちの目標は、

\ \ {\ displaystyle {\ vec {v '}} = q {\ vec {v}} q ^ { - 1} = \ left {\ frac {\ alpha} {2}} + {\ vec {u} {\ frac {\ alpha} {2}} {\ vec {u} {\ vec { }} \ sin {\ frac {\ alpha} {2}} \ right）} {\ vec {v '}} = q {\ vec {v}} q ^ { - 1} = \ left {\ frac {\ alpha} {2}} + {\ vec {u}} \ sin {\ frac {\ alpha {2}} \ right）\、{\ vec {v}} \、\ left {\ frac {\ alpha} {2}} - {\ vec {u}} \ sin {\ frac {\ alpha} {2}} \ right） ベクトルを生成する {\ displaystyle {\ vec {v}}} {\ vec {v}} ある角度だけ回転した {\ displaystyle \ alpha} \アルファ 軸周り {\ displaystyle {\ vec {u}}} {\ vec {u}}。展開すると、

{\displaystyle {\begin{aligned}{\vec {v'}}&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+({\vec {u}}{\vec {v}}-{\vec {v}}{\vec {u}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-{\vec {u}}{\vec {v}}{\vec {u}}\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-({\vec {v}}({\vec {u}}\cdot {\vec {u}})-2{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}(\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}})+({\vec {u}}\times {\vec {v}})(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}})+{\vec {u}}({\vec {u}}\cdot {\vec {v}})(2\sin ^{2}{\frac {\alpha }{2}})\\[6pt]&={\vec {v}}\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})(1-\cos \alpha )\\[6pt]&=({\vec {v}}-{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})\\[6pt]&={\vec {v}}_{\bot }\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {v}}_{\|}\end{aligned}}} {\ vec {v}}＆= {\ vec {v}} \ cos ^ {2} {\ frac {\ alpha} {2}} + {{vec {u}} { \ sin {\ frac {\ vec {u}}）\ sin {\ frac {\ alpha} {2}} \ cos {\ frac {\ alpha} {2}} - {vec { \ vec {v} {\ vec {u}} \ sin {2}} \\ [6pt]＆= {\ vec {v} } \ sin {\ frac {\ alpha} {2}} \ cos {2} {2}} {\ vec { {\ vec {u ve} {\ vec {u}} \ cdot {\ vec {u}}） - 2 {\ vec {u}} \ sin {2}} \\ [6pt]＆= {\ vec {v}} {sin {2}} {\ vec { （\ cos {2}} - \ sin {2} {\ frac {\ alpha} {2}}）+（{\ vec {u}} \ times {\ frac { （\ vec {u}}）（2 \ sin {\ frac {\ alpha} {2}} \ cos {\ frac {\ alpha} {2}}） {\ vec {v}} \ cos {alpha} {\ frac {\ alpha} {2}} \ cdot {\ vec {v}}） （1）（1）（2）のように、 - \ cos \ alpha）\\ [6pt]＆\ cos \ alpha +（{vec {u}} \ {vec {u}} \ {\ vec {u}} \ {\ vec {u ve} {\ vec {u ve} {\ vec {v}}）\ sin {alpha} {\ vec {v}}）\ sin \ alpha + {\ vec {v}} _ {\ ve} {end} {aligned}} どこで {\ displaystyle {\ vec {v}} _ {\ bot}} {\ vec {v}} _ {\ bot} そして {\ displaystyle {\ vec {v}} _ {\ |}} {\ vec {v}} _ {\ |}v →鉛直の成分とu →と平行な成分である。これは、u →軸の周りのαによる回転の公式です。

クォータニオン回転操作 このセクションで使用されているプロパティの正式な説明は、Altmanによって与えられています。[11]

回転の超球体 主な記事：回転グループSO（3） 回転の空間を視覚化する 単位四元数は表しグループユークリッドの回転で3次元を非常に簡単な方法で。回転と四元数の対応は、最初に回転の空間そのものを視覚化することで理解できます。

回転の空間における異なる角度と異なる軸による2つの回転。ベクトルの長さは、回転の大きさに関係します。 回転の空間を視覚化するために、より簡単なケースを考えることが役立ちます。3次元の任意の回転は、ある軸の周りのある角度による回転によって記述することができる。私たちの目的のために、私たちは角度のための手渡しを確立するために軸ベクトルを使用します。回転軸がxy平面内にある特殊なケースを考えてみましょう。これらの回転の1つの軸を、ベクトルが交差する円上の点で指定することができ、回転の角度を示すために円の半径を選択することができます。

同様に、回転軸がxy平面にある回転は、3次元の固定半径の球上の点として記述することができます。3次元空間の球の北極から、北極の点をアイデンティティ回転（ゼロ角回転）と指定します。ID回転の場合と同様に、回転軸は定義されておらず、回転角度（ゼロ）は無関係です。回転角が非常に小さい回転は、xyに平行な球を通るスライスによって指定することができます北極のすぐ近くにあります。このスライスによって定義される円は非常に小さく、回転の小さな角度に対応します。回転角が大きくなるにつれて、スライスはzの負の方向に移動し、球の赤道に達するまで円は大きくなり、180度の回転角に対応する。南に進むと、円の半径は小さくなります（負の数と見なされる回転の角度の絶対値に相当）。最後に、南極に達すると、円はもう一度、南極の点として指定された身元回旋に縮小されます。

この視覚化によって、そのような回転およびその表現の多くの特徴を見ることができることに留意されたい。回転の空間は連続的であり、各回転はほぼ同じ回転の近傍を有し、この近傍は近傍が縮小するにつれて平らになる。また、各回転は、球の中心を通る線の両端にある、球上の2つの対蹠点によって実際に表される。これは、各回転がある軸の周りの回転として、または反対方向を指す軸の周りの負の回転として表現され得るという事実を反映する（いわゆる二重カバー）。特定の回転角度を表す円の「緯度」は、その回転によって表される角度の半分であり、点が北から南極に移動するとき、緯度はゼロから180度の範囲にあり、回転角度0〜360度の範囲です。（ポイントの「経度」は特定の回転軸を表します）。ただし、この回転の組は合成では閉じられません。内軸を有する2つの連続した回転XY平面は、必ずしも、その軸にある回転与えないのXY平面を、したがって球面上の点として表現することができません。これは、回転が合成の中で閉じた集合を形成する3空間における一般的な回転の場合には当てはまらない。

"水平"軸（xy平面）を持つ回転の回転範囲。 この視覚化は、3次元空間における一般的な回転に拡張することができる。アイデンティティの回転は点であり、ある軸の周りの小さな回転角は、小さな半径を持つ球上の点として表すことができます。回転角が大きくなるにつれて、回転角が180度に達するまで球が成長し、球は収縮し始め、角度が360度（または負の方向から0度）に近づくとポイントになります。この一連の拡大および縮小球体は、4次元空間における超球体（3球）である。上記のより簡単な例と同様に、超球面上の点として表される各回転は、その超球面上の対角線点と一致します。超球面上の「緯度」は、対応する回転角の半分になり、近傍が縮小すると、任意の点の近傍が「フラット」（すなわち、3次元ユークリッド空間の点で表される）になる。この動作は、単位四元数の集合と一致します。一般四元数は、四次元空間内の点を表しますが、単位大きさを持つように制約することで、超球面に相当する三次元空間が得られます。単位四元数の大きさは、単位半径の超球に対応する単位である。単位四元数のベクトル部分は、回転軸に対応する2球の半径を表し、その大きさは、回転角の半分の余弦である。各回転は、2つの単位四元数の正反対の符号で表され、三次元の回転の空間におけるように、2つの単位四元数の四元数積は、単位四元数を生成する。また、単位クォータニオンの空間は、与えられた単位クォータニオンの任意の微小な近傍において「平坦」である。

回転の空間をパラメータ化する 我々は、緯度と経度のような2つの座標で球の表面をパラメータ化することができます。しかし、北極と南極では緯度と経度が悪い（縮退する）がありますが、極は球上の他の点と本質的に異なるわけではありません。極（緯度+ 90°と-90°）では、経度は無意味になります。

このような縮退を避けることができる2パラメータ座標系はないことが分かる。球を3次元空間に埋め込み、3つのデカルト座標（w、  x、  y）でパラメータ化し、北極を（w、  x、  y）=（1,0,0）に置くことで、南極は（w、  x、  y）=（-1,0,0）であり、w = 0、x 2 + y 2 = 1の赤道。球上の点が制約を満たすw 2 + x 2 + y 2 = 1であるので、3つの座標が存在するが、依然として2つの自由度しか持たない。球面上の点（w、  x、  y）は、ベクトル（x、  y、0）によって指示される水平軸の周りの通常空間における角度 {\ displaystyle \ alpha = 2 \ cos ^ { - 1} w = 2 \ sin ^ { - 1} {\ sqrt {x ^ {2} + y ^ {2}}}} \ alpha = 2 \ cos ^ { - 1} w = 2 \ sin ^ { - 1} {\ sqrt {x ^ {2} + y ^ {2}}}。

同様に、3D回転の超球面は3つの角度（オイラー角）でパラメータ化できますが、このようなパラメータ化はいずれも超球面上のある点で縮退し、ジンバルロックの問題につながります。我々は、4つのユークリッド座標を使用して、これを避けることができるwは、  X、  Y、  Zと、W 2 + X 2 + Y 2 + Z 2 = 1。点（w、  x、  y、  z）は、は、ベクトル（x、  y、  z）によって方向付けられた軸を中心とする角度 {\ displaystyle \ alpha = 2 \ cos ^ { - 1} w = 2 \ sin ^ { - 1} {\ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}}。} \α= 2 \ cos ^ { - 1} w = 2 \ sin ^ { - 1} {\ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}}。

回転で四元数のプロパティを説明する 非commutativity 四元数の乗算は非可換である。この事実は、どのように説明したp ↦ qはpをqは-1式を持つ、全く仕事ができるのQ Q -1 = 1を定義することによって。単位クォータニオンの乗算は3次元回転の構成に対応するので、この性質は一般的に3次元回転が可換でないことを示すことによって直観的にすることができる。

2つの本を隣に置く。そのうちの1つをz軸の周りに時計回りに90度回転させ、x軸を中心に180度反転させます。他の本をとり、最初にx軸を中心に180 度回転させ、z軸を中心に時計回りに90度回転させます。2冊の本は並行しない。これは、一般に、2つの異なる空間軸の周りの2つの異なる回転の構成が通勤しないことを示している。

オリエンテーション ベクトル外積軸角表現を定義するために使用さは、与えない向き空間に（「利き手」を）：3次元ベクトル空間において、式中の3つのベクトル ×  B = Cが常に右を形成します（または、クロス積がどのように定義されているかに応じて、左利きセット）、ベクトル空間に方向を固定します。あるいは、方向依存性は、軸ベクトルについての回転を指定するu →を参照して表現される。四元数形式の場合、空間の向きの選択は、乗算の次数に対応します。ij = kしかし、ji = -kである。一つの向きを反転させる場合、上記式は、となるP ↦ Q -1  のP Q、すなわち、単位Qは、軸方向のベクトルと同じ動作-共役四元数に置き換えられます。

他の回転表現との比較 四元数の利点 四元数（4つの数字）としての回転の表現は、直交行列（9つの数字）としての表現よりもコンパクトです。さらに、与えられた軸および角度に対して、対応する四元数を容易に構築することができ、逆に、四元数に対して軸および角度を容易に読み取ることができる。これらの両方は、行列またはオイラー角ではるかに困難です。

では、ビデオゲームや他のアプリケーション、1シーンがゆっくりシングルステップで回転してはならないことを意味し、「滑らかな回転」でしばしば興味を持っています。これは、クォータニオン内の球形線形補間のような曲線を選択することによって達成することができ、一方の端点は恒等変換1（またはその他の初期回転）であり、他方は意図する最終回転である。これは、他の回転表現ではより問題になります。

コンピュータ上で複数の回転を合成する場合、必ず丸め誤差が蓄積されます。わずかにオフの四元数は、正規化後の回転を表します。わずかにオフの行列はもはや直交しない可能性があり、適切な直交行列に変換するのは難しくなります。

クォータニオンはまた、ジンバルロックと呼ばれる現象を回避する。ジンバルロックは、例えばピッチ/ヨー/ロール回転システムにおいて、ピッチが上下に90°回転し、ヨーとロールが同じ動きに対応し、回転の自由が失われる。内ジンバル航空機は急ダイブ又は上昇している場合は、航空宇宙ベースの慣性航法システム、例えば、これは悲惨な結果を有することができます。

行列表現への変換と行列表現からの変換 四元数から直交行列へ 直交行列の単位四元数により回転に対応するZ = A + bの iは + のC  J + Dの K（と| Z | = 1  で与えられる列ベクトルと後掛ける場合）

2b-2adと2d + 2acと2cと2adとa ^ 2e-bとの間には、 2 ^ + {2} -b ^ {2} -c ^ {2} + d ^ {2} \\ \ end {pmatrix}}} R = {\ begin {pmatrix} a ^ {2} + b ^ {2} -c ^ {2} -d ^ {2}＆2bc-2ad＆2bd + 2ac \\ 2bc + 2ad＆a ^ {2} -b ^ {2 } + {2} -c ^ {2} + d ^ {2} \\ end {2} pmatrix}}。 この回転行列は、ベクトルwに対して次のように使用されます。 {\ displaystyle w_ {rotate} = R \ cdot w} w_ {回転} = R \ cdot w。この回転の四元数表現は次のように与えられます。

{bmatrix}} z ^ {*} {} {} {}}}}} { {bmatrix}}は、{bmatrix}} {0}} {\ begin {bmatrix}} \ end {bmatrix} どこで {\ displaystyle z ^ {*}} z ^ {*} 四元数の共役である {\ displaystyle z} z、 によって与えられた {\ displaystyle \ mathbf {z} ^ {*} = ab \ mathbf {i} -c \ mathbf {j} -d \ mathbf {k}} \ mathbf {z} ^ {*} = ab \ mathbf {i} -c \ mathbf {j} -d \ mathbf {k}

また、四元数の乗算は、（aとbが上記のzのような四元数であると仮定して）次のように定義されます。

a_ {0} {\ vec {b}} + b_ {0} {\ vec {b}} \ cdot {\ vec { vec {a}} + {\ vec {a}} \ times {\ vec {b}}}} ab =（a_ {0} b_ {0} - {\ vec {a}} \ cdot {\ vec {b}}; a_ {0} {\ vec {b}} + b_ {0} {\ vec {a }} + {\ vec {a}} \ times {\ vec {b}}）

2つのベクトルの外積が可換性ではないので、次数a、bは重要です。

直交行列からクォータニオンへ 回転行列のトレース（対角要素の和）がゼロまたは非常に小さい場合、いくつかの直接的な方法は不安定になる傾向があるため、回転行列を四元数に変換するときは注意が必要です。直交行列を四元数に変換する安定した方法については、回転行列の記事のQuaternionサブセクションを参照してください。

四元数をフィッティングする 上記のセクションでは、3 × 3回転行列Qからクォータニオンqを復元する方法について説明しました。しかし、例えば、丸め誤差のために純回転ではない行列Qがあり、Qを最も正確に表す四元数qを求めたいとします。その場合、我々は対称4 × 4行列 を構築する

Q_ {yx} + Q_ {xy}＆Q_ {zx} + Q_ {yx} + Q_ {xy} Q_ {yx}とQ_ {yy} -Q_ {xx} -Q_ {zz}とQ_ {zy} + Q_ {yz}とQ_ {yx} Q_ {xy}とQ_ {xy}との間には、Q_ {xz}とQ_ {yz} Q_ {yy} + Q_ {zz} \ end {bmatrix}}、}ここで、Q_ { Q_ {yx} + Q_ {yx} + Q_ {xy}とQ_ {zx} + Q_ {xz}は、 Q_ {yy} + Q_ {yy} -Q_ {xx} -Q_ {z}とQ_ {zy} + Q_ {yz} x_ {y}とQ_ {z}との間には、 Q_ {yx} + Q_ {yy} + Q_ {zz} \ end {bmatrix}}は、 最大の固有値に対応する固有ベクトル （x、  y、  z、  w）を見つける（Qが純粋な回転の場合にのみその値は1になる）。このようにして得られた四元数は、元の行列に最も近い回転に対応するQ [ 疑わしい - 議論 ] [12]

パフォーマンスの比較 このセクションでは、クォータニオンと他の方法（軸/角度または回転行列）を使用して3Dで回転を実行する際のパフォーマンスの影響について説明します。

結果 ストレージ要件 方法 ストレージ 回転行列 9 クォータニオン 3または4（下記参照） 角度/軸 3または4（下記参照） 回転は単位四元数で表されるので、四元数の構成要素のうち3つだけが独立しています。さらに計算するには、通常は4つの要素すべてが必要であるため、すべての計算で4番目のコンポーネントを回復するための追加費用が発生します。同様に、角度/軸は、単位方向に角度（またはその関数）を乗算することによって3成分ベクトルに格納することができるが、これは計算に使用するときに追加の計算コストがかかる。

回転連鎖操作の性能比較 方法 ＃multiplies ＃を追加/減算する トータルオペレーション 回転行列 27 18 45 クォータニオン 16 12 28 ベクトル回転操作の性能比較[13] [14] 方法 ＃multiplies ＃を追加/減算する ＃sin / cos トータルオペレーション 回転行列 9 6 0 15 クォータニオン* 15 15 0 30 角度/軸 18 12 2 30 + 2

• 注：クォータニオンは回転行列のような行列（12の乗算と12の加算/減算）に暗黙的に変換できます。

使用されるメソッド ベクトルv →を回転するには、3つの基本的なアプローチがあります。

3×3 回転行列 Rとv →を表す元の3×1 列行列の行列積を計算する。これは、ベクトルを回転させる最も効率的な方法である3×（3回の乗算+2回の加算）= 9回の乗算と6回の加算を必要とする。 回転は、スカラ（実数）部分wとベクトル（虚数）部分r →を持つ単位長四元数q =（w、  r →）で表すことができます。回転は、式を介して3Dベクトルv →に適用することができます \ times {\ vec {r}} \ times {\ vec {r}} \ times {\ vec {r}} {v}} + w {\ vec {v}}）} {times} \ times {\ vec {v} {\ vec {r}} \ times {\ vec { } + w {\ vec {v}}）。これは、評価するために15回の乗算と15回の加算が必要です（2の係数が乗算によって行われる場合は18回の乗算と12回の加算が必要です）。この式はもともと軸/角度表記（Rodriguesの公式）四元数表記に適用されます。これは、より効率的ではなくよりコンパクトな四元数乗法の式と同じ結果をもたらす {\ displaystyle {\ vec {v}} _ {\ text {new}} = q {\ vec {v}} q ^ { - 1}} {\ vec {v}} _ {\ text {new}} = q {\ vec {v}} q ^ { - 1}。 使用角度/軸式に角度/軸に変換する回転行列 Rは、次いでベクターを乗じ、回転行列に四元表記を変換するための式を使用し、同様に、ベクターを乗算、または。角度/軸をRに変換すると、12の乗算、2つの関数呼び出し（sin、cos）、および10の加算/減算が行われます。項目1から、Rを使用して回転すると、合計21の乗算、16の加算/減算、2つの関数呼び出し（sin、cos）に対して、9回の乗算と6回の加算が追加されます。四元数をRに変換するには、12の乗算と12の加算/減算が必要です。項目1から、Rを使用して回転する 合計21回の乗算と18回の加算/減算のために9回の乗算と6回の加算が追加されます。 4D空間での回転としてのユニット四元数の対 1組の単位四元数z lおよびz rは、4D空間における任意の回転を表すことができる。4次元ベクトルを考えるのV →を、そしてそれが四元数であることをふり、我々はベクトル回転させることができるのV →このように：

\ mathbf {z} _ {\ rm {r}} {\ vec {v}} \ mathbf { {{{{{{{{{{{{}} {{{{{{{}} {{{{{{{}} {{{{{{{}}} {{{{{{{}}} { }}＆a _ {\ rm {l}}＆a d _ {\ rm {l}}＆c _ {\ rm {1}} \\ c _ {l}}＆a_ {\ rm {1}}＆a_ {\ rm {l}}＆a_ {r} \ end {prm} {\ begin {p}} {end {p}} {\ r { \ _ {\ rm} \ - {\ rm} \ - {\ rm} \ rm {r}}＆a_ {r r}}＆b _ {\ rm {r}} \\ d_ {\ rm} ＆a {\ rm {r}} \ end {pmatrix}} {\ begin {pmatrix} w \\ x \\ y \\ z \ end {pmatrix}}} \ mathbf {\ vec {v}}）= \ mathbf {z} _ {\ rm {1}} \ mathbf {z} _ {\ rm {r}} = {\ begin {pmatrix } \\ b {{\ rm {1}}＆a_ {\ rm {1}} \ {\ rm {l}}＆d {\ rm {l}}＆a {_ rm {l}} \\ c_ { } \ {\ rm {1}} \ -d {{\ rm {1}} \ {\ rm} {\ rm} {\ rm} {\ rm {r} {\ rm} {\ rm} {\ rm} {\ rm} {\ rm {r} {\ rm} \ rm {r}}＆a_ {\ rm}＆a_ {\ rm {r}}＆a_ {\ rm} rm {r}} \ end {pmatrix}} {\ begin {pmatrix} w \\ x \\ y \\ z \ end {pmatrix}} 行列の対はℝの回転表す4。なお、 \ mathbf {z} _ {\ rm {r}} = \ mathbf {z} _ {\ rm {l} }}（{\ vec {v}} \ mathbf {z} _ {\ rm {r}}}} （\ mathbf {z} _ {\ rm {1}}）\ mathbf {z} _ {\ rm {r}} = \ mathbf { {\ vec {v}} \ mathbf {z} _ {\ rm {r}}）2つの行列は通勤する必要があります。したがって、4次元回転の集合の2つの通勤サブグループが存在する。任意の4次元回転は6自由度を持ち、各行列は6自由度のうちの3つを表します。

4次元回転のジェネレータは、（以下のように）クォータニオンの対によって表すことができるので、すべての4次元回転も表現することができる。

\ mathbf {z} _ {\ rm {r}} = {\ begin {pmatrix} 1＆-dt_ {ab}＆ dt_ {ab}＆1＆-dt_ {bc}＆ - dt_ {bd} \\ dt_ {ac}＆dt_ {bc}＆1＆-dt_ {cd} \\ dt_ {ad }＆dt_ {bd}＆dt_ {cd}＆1 \ end {pmatrix}} {\ begin {pmatrix} w \\ x \\ y \\ z \ end {pmatrix}}} \ mathbf {z} _ {\ rm {1}} \ mathbf {z} _ {\ rm {r}} = {\ begin {pmatrix} 1＆-dt_ {ab}＆ - dt_ { dt_ {ab}＆ - dt_ {ab}＆ - dt_ {bd} \\ dt_ {ac}＆dt_ {bc}＆1＆-dt_ {cd} \\ dt_ {ad}＆dt_ { bd}＆dt_ {cd}＆1 \ end {pmatrix}} \ begin {pmatrix} w \\ x \\ y \\ z \ end {pmatrix}} i + {dt_ {ac} -dt_ {bd} \ over 2} j + {dt_ {ab} + dt_ {cd} \ over 2} dt_ {ad} + dt_ {bc} \ over 2} k} \ mathbf {z} _ {\ rm {1}} = 1+ {dt_ {ab} + dt_ {cd} \ over 2} i + {dt_ {ac} -dt_ {bd} \ over 2} j + {dt_ {ad } + dt_ {bc} \ over 2} k i + {dt_ {ac} + dt_ {bd} \ over 2} j + {dt_ {ab} -dt_ {cd} dt_ {ad} -dt_ {bc} \ over 2} k} \ mathbf {z} _ {\ rm {r}} = 1+ {dt_ {ab} -dt_ {cd} \ over 2} i + {dt_ {ac} + dt_ {bd} \ over 2} j + {dt_ {ad } -dt_ {bc} \ over 2} k 関連項目 アンチツイスター機構 2元多面体群 ビキータニ SOのチャート（3） クリフォード代数 四元数とオイラー角の変換 スペースをカバーする 二重四元数 楕円形状 3次元の回転形式 回転（数学） スピングループ スラップ、球面線形補間 Olinde Rodrigues ウィリアム・ロワン・ハミルトン 参考文献

ケンShoemake（1985）。「クォータニオンカーブを使用したアニメーションの回転」 （PDF） 。コンピュータグラフィックス。19（3）：245-254。doi： 10.1145 / 325165.325242。SIGGRAPH '85で発表されました。
JM McCarthy、1990、MIT Pressの理論キネマティクス入門
アムノンカッツ（1996）計算硬質ビークルダイナミクス、クリーガー出版社 ISBN978から1575240169 
JB Kuipers（1999）四元数と回転シーケンス：軌道、航空宇宙、バーチャルリアリティへの応用を備えた入門書、プリンストン大学出版局 ISBN978-0-691-10298-6 
カルステンクンツェ、ヘルムートSchaeben（2004年11月）。"クォータニオンのビンガム分布とテクスチャ解析における球状ラドン変換"。数学的地質学。8：917-943を参照のこと。doi： 10.1023 / B：MATG.0000048799.56445.59。

「comp.graphics.algorithmsよくあるご質問」を。2017年7月2日に取得されました。

ロドリゲス、O.（1840）、デLOISgéométriquesQUIrégissentレdéplacementsD'UN SYSTEME SOLIDE DANSレスパス、らラ変動デcoordonnéesprovenantデSESdéplacementsコンsidérésindépendammentデ原因quiのpeuventレproduire、ジャーナル・デをMathématiquesPures etAppliquéesde Liouville 5、380-440。
ウィリアム・ローワン・ハミルトン（1850年から1844年）の四元または代数における虚数の新システムでは、哲学の雑誌、のDavid R.ウィルキンスのコレクションへのリンクトリニティカレッジ、ダブリン
リー、ビョンウク（1991）、 "四元、付録Bとの差別化" （PDF）を、 PhはD.論文、頭蓋骨のランドマークのステレオマッチング、スタンフォード大学。：57-58
Altmann、Simon L. "Hamilton、Rodrigues、およびQuaternion Scandal"に。数学マガジン。62（5）：306、 doi： 10.2307 / 2689481。
Simon L. Altman（1986）の回転、四元数、および二重グループ、Dover Publications（特に12章を参照）にください。
バー-Itzhack、Itzhack Y.（2000年11月- 12月）、 "回転行列から四元を抽出するための新しい方法"、ガイダンス、コントロールとダイナミクスのAIAAジャーナル、 23（6）：1085、 Bibcode： 2000JGCD。 ..23.1085B、 doi： 10.2514 / 2.4654、 ISSN  0731-5090
Eberly、D.、回転表現とパフォーマンスの問題

https://bitbucket.org/eigen/eigen/src/4111270ba6e10882f8a8c571dbb660c8e9150138/Eigen/src/Geometry/Quaternion.h?at=default&fileviewer=file-view-default#Quaternion.h-469 Grubin、Carl（1970）。"オイラーの軸と角度による四元数計画の導出"。J.スペーククラフトロケット。7（10）。pp。1261-1263。Bibcode：1970JSpRo ... 7.1261G。doi：10.2514 / 3.30149。 Battey-Pratt、EP; Racey、TJ（1980）。"基本粒子の幾何学モデル"。理論物理学の国際ジャーナル。19（6）。Bibcode：1980IJTP ... 19..437B。doi：10.1007 / BF00671608。 Arribas、M。Elipe、A。Palacios、M.（2006）。「四元数と剛体の回転」天体メック。Dyn。Astr。96：239-251。Bibcode：2006CeMDA..96..239A。doi：10.1007 / s10569-006-9037-6。 外部リンクとリソース Shoemake、Ken。"四元数" （PDF）。 "シンプルクォータニオン型と30以上のコンピュータ言語での操作"。上のロゼッタコード Hart、John C. "Quaternion Demonstrator"。 Dam、Eik B .; コッホ、マーティン; Lillholm、Martin（1998）。"四元数、補間およびアニメーション" （PDF） 。 Leandra、Vicci（2001）。「3-空間における四元数とローテーション：代数と幾何学的解釈」 （PDF） 。 ハウエル、トーマス; Lafon、Jean-Claude（1975）。「クォータニオン製品の複雑さ、TR75-245」 （PDF） 。コーネル大学。 Horn、Berthold KP（2001）。「ユニット四元数と回転にいくつかの注意事項」 （PDF） 。 イ・ビョンウク（Lee、Byung-Uk、1991）。単位四元数の回転表現 - 付録A、四元数との区別 - 付録B （PDF）（博士論文）スタンフォード大学。 ヴァンス、ロッド "接続されたLieグループのいくつかの例"。 カテゴリー：クォータニオン3次元での回転剛体力学3Dコンピュータグラフィックス