掛谷集合

数学において掛谷集合（かけやしゅうごう、英: Kakeya set）もしくはベシコビッチ集合（英: Besicovitch set）とは、ユークリッド空間において、全ての方向に単位線分を持つ点の集合のことである。名称は掛谷宗一およびアブラム・ベシコヴィッチに因む。任意の正の数よりも小さい測度の掛谷集合が存在する。

平面において単位線分を連続的な移動により180度回転させて、線分を元の位置に向きを逆転させて戻すことができる点の集合を掛谷針集合と呼ぶ。

ベシコビッチの針集合

「ペロンツリーの成長」: 小さな測度の掛谷集合を構築する方法。ここでは、三角形を分割し、重なり合わせる二つの方法が示されている。最初は二つの三角形を使う方法で、次は八つの三角形を使う方法である。この方法は、元の三角形を $2^{n}$ 個の部分に切り分けることで、任意に小さな集合を構築するために使用できる。詳細については、 を参照のこと。

ベシコビッチは、単位長の針が回転できるような領域 $D$ の面積に対して、0より大きい下限が存在しないことを示した。すなわち、すべての $\varepsilon >0$ に対して、面積 $\varepsilon$ の領域が存在し、その中で針が連続的に動いて360度完全に回転することができる。これは、すべての方向に単位セグメントを含む平面集合に関する彼の以前の研究に基づいている。そのような集合は現在「ベシコビッチ集合」と呼ばれている。ベシコビッチが任意に小さい 測度 を持つこのような集合を示したのは1919年のことであった。この問題はそれ以前から解析学者によって考えられていた可能性がある。

ベシコビッチ集合を構築する一つの方法（対応する図を参照）は、オスカー・ペロンにちなんで「ペロンツリー」と呼ばれ、ベシコビッチの元の構築法を簡略化することができた。正確な構築法と数値的な上限は、ベシコビッチの普及書に記載されている。

最初に観察すべきことは、針が直線上をどれだけ遠くまで動くことができるかということである。これは、針が幅ゼロの線分だからである。次のトリックはパールによって知られる「パール結合」であり、針をほとんど面積を掃かずに平行な二つの位置の間で移動させる方法を説明しする。針は「N」の形に沿って動く。最初の位置から「N」の左側を$r$だけ上に移動し、中間の対角線に角度を掃き出し、対角線を下に移動し、二つ目の角度を掃き出し、その後「N」の右側を平行に上に移動して、必要な二つ目の位置に到達する。非ゼロの面積が掃かれる領域は、一つの高さの三角形と「N」の頂点の角度の二つだけとなる。掃かれる面積はこの角度に比例しており、これは $1/r$ に比例する。

構築は、高さ1の任意の三角形から始まり、針が容易に掃くことができる上部にかなりの角度がある。この三角形に対して多くの操作を行い、その面積を小さくしながら針が掃くことができる方向を同じに保つことが目標となる。 まず、三角形を二つに分け、それらの基部が重なり合い、全体の面積を最小限に抑えるように変形する。針は、最初の三角形によって与えられた方向を掃き出し、二つ目の三角形にジャンプして、その後二つ目の三角形によって与えられた方向を掃き出すことで、同じ方向を掃き出すことができる。針は、「N」技術を使用して三角形をジャンプすることができる。元の三角形が切られた二つの線は平行であることからこれが可能となる。

三角形を 2ⁿ 個の部分三角形に分割すると仮定する。図には八つの三角形が示されている。 各連続した三角形のペアに対して、前述の重なりの操作を実行し、新しい形状を半分作る。それぞれが二つの重なり合った三角形からなる新しい形状となる。次に、これらの新しい形状の連続したペアを、全体の面積を最小限に抑えるように基部が重なり合うようにシフトして重ねる。この操作を n 回繰り返し、一つの形状だけになるまで続ける。再び、針はそれぞれの 2ⁿ の部分三角形の方向の順序に沿って同じ方向を掃き出すことができる。針は、これらの三角形が切られた二つの線が平行であるため、連続した三角形を「N」技術でジャンプできる。

残るのは、最終形状の面積を計算することである。証明は難しいので省略する。代わりに、数がどのようになるかを説明する。 図を見れば、2ⁿ の部分三角形が多く重なり合っていることがわかる。すべての部分三角形は底で重なり合い、半分は左の枝の底で、四分の一は左の左の枝の底で、と同様に続く。 i 回の統合操作から作成された各形状の面積が A_i で制限されると仮定する。 二つの形状を統合する前は、面積は 2A_i に制限される。 次に、二つの形状をできるだけ重なるように移動させる。 最悪のケースでは、これら二つの領域は、互いに直交する二つの 1 by ε の長方形であり、その重なり合う面積はわずか ε² である。しかし、長く細い形状の二つの形状は、連続した部分三角形のグループから作られているため、大部分が同じ方向を指す。ここでの主張は、これらが面積の少なくとも 1% が重なるということである。したがって、統合された面積は次のように制限される。

A_i+1 = 1.99 A_i。元の三角形の面積は 1 に制限されている。したがって、各部分三角形の面積は次のように制限される。

A₀ = 2^-n であり、最終的な形状の面積は次のように制限される。

A_n = 1.99ⁿ × 2^-n。実際には、重なり合わないすべての面積を注意深く合計すると、最終的な領域の面積はずっと大きく、すなわち 1/n になる。 n が増加するにつれて、この面積はゼロに収束する。 ベシコビッチ集合は、正三角形から作成されたペロンツリーの六つの回転を組み合わせることによって作成できる。 平行四辺形を使用しても同様の構築が可能である。

他にも「成長」法以外で測度ゼロのベシコビッチ集合を構築する方法がある。 例えば、カハーヌは、カントール集合を用いて二次元平面における測度ゼロのベシコビッチ集合を構築している。

ペロンツリーから構築された掛谷針集合。

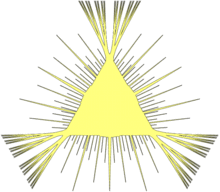
1941年、H. J. ヴァン・アルフェンは、半径 2 + ε（任意の ε > 0）を持つ円の中に任意に小さな掛谷針集合が存在することを示した。1965年には、より小さい面積の単連結掛谷針集合が発見された。メルビン・ブルームとI. J. ショーンバーグは独立に、面積が ${\tfrac {\pi }{24}}(5-2{\sqrt {2}})$ に近づく掛谷針集合を発表した。この数値は「ブルーム・ショーンバーグ数」と呼ばれている。ショーンバーグは、この数が単連結掛谷針集合の面積の下限であると予想した。しかし、1971年には F. カニンガムは、ε > 0 が与えられたとき、半径 1 の円に含まれる面積が ε より小さい単連結掛谷針集合が存在することを示した。

任意に小さい正の測度を持つ掛谷針集合と測度ゼロのベシコビッチ集合は存在するが、測度ゼロの掛谷針集合は存在しない。

掛谷針集合の諸定理

任意の正の数よりも小さい面積の掛谷針集合が存在する。

最小の凸掛谷針集合は一辺 ${2/{\sqrt {3}}}$ の正三角形である。

半径 1 の円の内部で任意の正の実数 ε に対し ${\tfrac {\pi }{108}}$+ε 以下の面積を持つ単連結掛谷針集合が存在する。

掛谷予想

定義

これらのベシコビッチ集合がどれほど小さくなり得るかという同様の問題が高次元で提起され、「掛谷予想」として知られるいくつかの予想が生まれ、幾何測度論と呼ばれる数学の分野の発端となった。特に、測度ゼロのベシコビッチ集合が存在する場合、これらはそれらが存在する空間の次元よりも小さい次元の s 次元 ハウスドルフ測度がゼロである可能性があるのか？という問題が生じる。この問題は次の予想を導く：

掛谷集合予想: Rⁿ における ベシコビッチ集合 を、あらゆる方向に単位線分を含む集合として定義する。そのような集合は必ず ハウスドルフ次元 と ミンコフスキー次元 が n に等しいか？

これは n = 1 および 2 の場合に真であることが知られているが、高次元の場合には部分的な結果しか知られていない。

掛谷最大関数

この問題に対する現代的なアプローチの一つは、次のように構成される特定のタイプの 最大関数 を考慮することである：Sⁿ⁻¹ ⊂ Rⁿ を n 次元空間の単位球面とする。$T_{e}^{\delta }(a)$ を長さ 1、半径 δ > 0 の円柱として定義し、点 a ∈ Rⁿ の中心にあり、その長い側が単位ベクトル e ∈ Sⁿ⁻¹ の方向に平行である。次に、局所可積分 関数 f に対して、f の 掛谷最大関数 を次のように定義する。

$f_{*}^{\delta }(e)=\sup _{a\in \mathbf {R} ^{n}}{\frac {1}{m(T_{e}^{\delta }(a))}}\int _{T_{e}^{\delta }(a)}|f(y)|dm(y)$

ここで m は n 次元 ルベーグ測度 を表す。$f_{*}^{\delta }$ は球面 Sⁿ⁻¹ 内のベクトル e に対して定義されている。

次に、これらの関数に対して次の予想がある。これが真であれば、より高次元の掛谷集合予想を示唆する：

掛谷最大関数予想: 任意の ε > 0 に対して、任意の関数 f とすべての δ > 0 に対して次のような定数 C_ε > 0 が存在する：

$\left\|f_{*}^{\delta }\right\|_{L^{n}(\mathbf {S} ^{n-1})}\leqslant C_{\epsilon }\delta ^{-\epsilon }\|f\|_{L^{n}(\mathbf {R} ^{n})}.$

結果

掛谷予想を証明するためのいくつかの結果は次の通りである：

• 掛谷予想は n = 1 （自明に）および n = 2（Davies）の場合に真である。
• 任意の n 次元空間において、Wolff は、掛谷集合の次元は少なくとも (n+2)/2 であることを示した。
• 2002年、Katz と Tao はWolffの境界を $(2-{\sqrt {2}})(n-4)+3$ に改善し、n > 4 に対してより良くなった。
• 2000年、Katz、Łaba、および Tao は、3次元の掛谷集合の ミンコフスキー次元 が 5/2 よりも厳密に大きいことを証明した。
• 2000年、Jean Bourgain は掛谷問題を 算術組合せ論 に関連付け、調和解析および 加法的数論を含む問題に発展させた。
• 2017年、Katz と Zahl は3次元のベシコビッチ集合の ハウスドルフ次元 の下限を $5/2+\epsilon$ に改善した。ただし絶対定数 $\epsilon >0$ とする。

解析への応用

やや驚くべきことに、これらの予想は、特に調和解析における他のいくつかの問題に関連していることが示されている。例えば、1971年にチャールズ・フェッファーマンは、ベシコビッチ集合の構成を利用して、次のことを示した。次元が1を超える場合、原点を中心とした半径が無限大に向かう球体上で取られるトランケート・フーリエ積分は、L^pノルム（p ≠ 2の場合）で収束しないことがある（これは、一次元の場合においてそのようなトランケート積分が収束するのとは対照的である）。

掛谷問題の類似および一般化

円や球を含む集合

掛谷問題の類似として、直線以外のより一般的な形状を含む集合を考えることがある。例えば、円を考える。

• 1997年および1999年、ウルフは、すべての半径の球を含む集合は完全な次元を持たなければならず、つまり、その次元は存在する空間の次元と等しいことを示した。これは、掛谷最大関数に類似した円の最大関数に対しての境界を証明することによって証明された。

• 半径ゼロの周りの球を含む集合が存在するという予想が立てられた。エリアス・スタインの結果 は、n ≥ 3のとき、すべてのそのような集合は正の測度を持たなければならないことを証明した。また、マーストランドは、n=2の場合でも同様のことを証明した。

k次元ディスクを含む集合

掛谷予想の一般化として、すべての方向における直線のセグメントの代わりに、k次元部分空間の部分を含む集合を考える。(n, k)-ベシコビッチ集合 Kを、レベーグ測度がゼロであるRⁿ内のコンパクトな集合と定義する。つまり、Bを原点を中心とする単位球とし、任意のk次元部分空間Pに対して、P ∩ Bに対してx ∈ Rⁿが存在し、(P ∩ B) + x ⊆ Kとなるようにする。したがって、(n, 1)-ベシコビッチ集合は、先に述べた標準的なベシコビッチ集合である。

(n, k)-ベシコビッチ予想: k > 1の場合、(n, k)-ベシコビッチ集合は存在しない。

1979年、マーストランド は、(3, 2)-ベシコビッチ集合が存在しないことを証明した。同時期に、ケネス・ファルコナー は、2k > nの場合、(n, k)-ベシコビッチ集合が存在しないことを証明した。これまでの最良の境界はブルゲインによって、2^k−1 + k > nの場合には、そのような集合は存在しないことが証明されている。

有限体上の掛谷集合

1999年、ウルフは掛谷問題の有限体に関する類似問題を提起し、この予想を解決するための技法がユークリッドの場合にも応用できることを期待した。

有限体掛谷予想: Fを有限体とし、K ⊆ Fⁿを掛谷集合とする。すなわち、任意のベクトルy ∈ Fⁿに対して、Kが直線{x + ty : t ∈ F }を含むようにするためのx ∈ Fⁿが存在する。このとき、集合Kは少なくともc_n|F|ⁿのサイズを持つ。ここでc_n>0はnのみに依存する定数である。

ゼエブ・ディヴィールは2008年にこの予想を証明した。彼は、c_n = 1/n!のときにこの命題が成り立つことを示した。 彼の証明では、n変数の任意の次数が|F|未満の多項式が掛谷集合上でゼロになる場合、それは恒等的にゼロである必要があることを示した。一方、n変数の次数が|F|未満の多項式は次元が

${|\mathbf {F} |+n-1 \choose n}\geq {\frac {|\mathbf {F} |^{n}}{n!}}.$

となるベクトル空間を形成する。したがって、与えられた集合がこの数未満の点を持つ場合、次数が|F|未満の非自明な多項式が少なくとも1つ存在することになる。これら2つの観察を組み合わせることで、掛谷集合は少なくとも|F|ⁿ/n!の点を持たなければならないことが示される。

この技法が元の掛谷予想を証明するために拡張されるかどうかは不明だが、この証明は本質的に代数的な反例がありそうにないことから、元の予想の信憑性を高めている。ディヴィールは、有限体の掛谷問題に関する進展とそのランダムネス抽出器との関係に関する調査記事を執筆した。

掛谷針集合の例

半径 0.5 の円板 $s\approx 0.78539$

幅 1 のルーローの三角形 $s\approx 0.70477$

一辺 ${2/{\sqrt {3}}}$ の正三角形 $s\approx 0.57735$

半径 3 / 4 の円に内接するデルトイド $s\approx 0.39270$

外部リンク

• Kakeya at University of British Columbia
• Besicovitch at UCLA
• Kakeya needle problem at mathworld
• Dvir’s proof of the finite field Kakeya conjecture at Terence Tao's blog
• An Introduction to Besicovitch-Kakeya Sets