「共役勾配法」の版間の差分
編集の要約なし |
m 外部リンクの修正 http:// -> https:// (www.cs.cmu.edu) (Botによる編集) |
||
| (41人の利用者による、間の55版が非表示) | |||
| 1行目: | 1行目: | ||
[[ファイル:Conjugate gradient illustration.svg|right|thumb|線型方程式の二次形式を最小化するための、最適なステップサイズによる[[最急降下法]](緑)の収束と共役勾配法(赤)の収束の比較。共役勾配法は、厳密には''n''次の係数行列に対して高々''n''ステップで収束する(ここでは''n''=2)。]] |
|||
'''共役勾配法'''('''Conjugated gradient method'''):数値最適化の一手法。[[最急降下法]]より計算の効率は高い。 |
|||
'''共役勾配法'''(きょうやくこうばいほう、{{lang-en-short|''conjugate gradient method''}}、CG法とも呼ばれる)は[[対称行列|対称]][[正定値行列|正定値]]行列を係数とする[[連立一次方程式]]を解くための[[アルゴリズム]]である<ref name="Yamamoto1">{{Cite book |和書 |author=山本哲朗 |title=数値解析入門 |edition=増訂版 |date=2003-06 |publisher=[[サイエンス社]] |series=サイエンスライブラリ 現代数学への入門 14 |ISBN=4-7819-1038-6}}</ref><ref name="mori">[[森正武]]. 数値解析 第2版. [[共立出版]].</ref><ref name="hpc">数値線形代数の数理と[[高性能計算|HPC]], 櫻井鉄也, 松尾宇泰, 片桐孝洋編(シリーズ応用数理 / [[日本応用数理学会]]監修, 第6巻)[[共立出版]], 2018.8</ref><ref name="clang">皆本晃弥. (2005). UNIX & Informatioin Science-5 C 言語による数値計算入門.</ref>。[[反復法 (数値計算)|反復法]]として利用され<ref name="Yamamoto1"/><ref name="mori"/><ref name="hpc"/><ref name="clang"/>、[[コレスキー分解]]のような直接法では大きすぎて取り扱えない、大規模な[[疎行列]]を解くために利用される。そのような問題は[[偏微分方程式]]などを数値的に解く際に常に現れる<ref name="Yamamoto1"/><ref name="tabata">田端正久; 偏微分方程式の数値解析, 2010. 岩波書店.</ref><ref name="to">登坂宣好, & 大西和榮. (2003). 偏微分方程式の数値シミュレーション. 東京大学出版会.</ref><ref>Zworski, M. (2002). Numerical linear algebra and solvability of partial differential equations. Communications in mathematical physics, 229(2), 293-307.</ref>。 |
|||
共役勾配法は、エネルギー最小化などの[[最適化問題]]を解くために用いることもできる<ref>Gill, P. E., Murray, W., & Wright, M. H. (1991). Numerical linear algebra and optimization (Vol. 1, p. 74). Redwood City, CA: Addison-Wesley.</ref><ref>Gilbert, J. C., & Nocedal, J. (1992). Global convergence properties of conjugate gradient methods for optimization. SIAM Journal on optimization, 2(1), 21-42.</ref><ref>Steihaug, T. (1983). The conjugate gradient method and trust regions in large scale optimization. SIAM Journal on Numerical Analysis, 20(3), 626-637.</ref>。 |
|||
==関連記事== |
|||
{{仮リンク|双共役勾配法|en|Biconjugate gradient method}}は、共役勾配法の非対称問題への拡張である<ref>Black, Noel and Moore, Shirley. "Biconjugate Gradient Method." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. {{URL|https://mathworld.wolfram.com/BiconjugateGradientMethod.html}}</ref>。また、非線形問題を解くために、さまざまな[[非線形共役勾配法]]が提案されている<ref>Dai, Y. H. (2010). Nonlinear conjugate gradient methods. Wiley Encyclopedia of Operations Research and Management Science.</ref><ref>Hager, W. W., & Zhang, H. (2006). A survey of nonlinear conjugate gradient methods. Pacific journal of Optimization, 2(1), 35-58.</ref><ref>Dai, Y., Han, J., Liu, G., Sun, D., Yin, H., & Yuan, Y. X. (2000). Convergence properties of nonlinear conjugate gradient methods. SIAM Journal on Optimization, 10(2), 345-358.</ref>。 |
|||
*[[計算工学]] |
|||
*[[代数学]] |
|||
==詳説== |
|||
対称正定値行列'''A'''を係数とする''n''元連立一次方程式 |
|||
{{Indent|'''Ax''' <nowiki>=</nowiki> '''b'''}} |
|||
の解を'''x'''<sub>*</sub>とする。 |
|||
===直接法としての共役勾配法=== |
|||
非零ベクトル'''u'''、'''v'''が |
|||
{{Indent|<math> \mathbf{u}^{\mathrm{T}} \mathbf{A} \mathbf{v} = \mathbf{0}</math>}} |
|||
を満たすとき、'''u'''、'''v'''は'''A'''に関して共役であるという<ref name="mori"/><ref name="hpc"/><ref name="clang"/>。'''A'''は対称正定値なので、左辺から内積 |
|||
{{Indent|<math> \langle \mathbf{u},\mathbf{v} \rangle_\mathbf{A} := \langle \mathbf{A}^{\mathrm{T}} \mathbf{u}, \mathbf{v}\rangle = \langle \mathbf{A} \mathbf{u}, \mathbf{v}\rangle = \langle \mathbf{u}, \mathbf{A}\mathbf{v} \rangle = \mathbf{u}^{\mathrm{T}} \mathbf{A} \mathbf{v}</math>}} |
|||
を定義することができる。この内積に関して2つのベクトルが直交するなら、それらのベクトルは互いに共役である。 |
|||
この関係は対称で、'''u'''が'''v'''に対して共役なら、'''v'''も'''u'''に対して共役である(この場合の「共役」は[[複素共役]]と無関係であることに注意)。 |
|||
{'''p'''<sub>''k''</sub>}を''n''個の互いに共役なベクトル列とする。'''p'''<sub>''k''</sub>は[[基底 (線型代数学)|基底]]'''R'''<sup>''n''</sup>を構成するので、'''Ax''' = '''b'''の解'''x'''<sub>''*''</sub>をこの基底で展開すると、 |
|||
{{Indent|<math> \mathbf{x}_* = \sum^{n}_{i=1} \alpha_i \mathbf{p}_i</math>}} |
|||
と書ける。ただし係数は |
|||
{{Indent|<math> \mathbf{A}\mathbf{x}_* = \sum^{n}_{i=1} \alpha_i \mathbf{A} \mathbf{p}_i = \mathbf{b}.</math><br /> |
|||
<math> \mathbf{p}_k^{\mathrm{T}} \mathbf{A}\mathbf{x}_* = \sum^{n}_{i=1} \alpha_i\mathbf{p}_k^{\mathrm{T}} \mathbf{A} \mathbf{p}_i= \mathbf{p}_k^{\mathrm{T}} \mathbf{b}.</math><br /> |
|||
<math> \alpha_k = \frac{\mathbf{p}_k^{\mathrm{T}} \mathbf{b}}{\mathbf{p}_k^{\mathrm{T}} \mathbf{A} \mathbf{p}_k} = \frac{\langle \mathbf{p}_k, \mathbf{b}\rangle}{\,\,\,\langle \mathbf{p}_k, \mathbf{p}_k\rangle_\mathbf{A}} = \frac{\langle \mathbf{p}_k, \mathbf{b}\rangle}{\,\,\,\|\mathbf{p}_k\|_\mathbf{A}^2}. </math>}} |
|||
で与えられる。 |
|||
この結果は、上で定義した内積を考えるのが最も分かりやすいと思われる。 |
|||
以上から、'''Ax''' = '''b'''を解くための方法が得られる。すなわち、まず''n''個の共役な方向を見つけ、それから係数α<sub>''k''</sub>を計算すればよい。 |
|||
===反復法としての共役勾配法=== |
|||
共役なベクトル列'''p'''<sub>''k''</sub>を注意深く選ぶことにより、一部のベクトルから'''x'''<sub>*</sub>の良い近似を得られる可能性がある。そこで、共役勾配法を反復法として利用することを考える<ref name="mori"/><ref name="hpc"/><ref name="clang"/>。こうすることで、''n''が非常に大きく、直接法では解くのに時間がかかりすぎるような問題にも適用することができる。 |
|||
'''x'''<sub>*</sub>の初期値を'''x'''<sub>0</sub> = 0 とする。'''x'''<sub>*</sub>が[[二次形式]] |
|||
{{Indent|<math> f(\mathbf{x}) = \frac12 \mathbf{x}^{\mathrm{T}} \mathbf{A}\mathbf{x} - \mathbf{b}^{\mathrm{T}} \mathbf{x} , \quad \mathbf{x}\in\mathbf{R}^n. </math>}} |
|||
を最小化する一意な解であることに注意し、最初の基底ベクトル'''p'''<sub>1</sub>を'''x''' = '''x'''<sub>0</sub>での''f''の勾配'''Ax'''<sub>0</sub>−'''b'''='''−b'''となるように取る。このとき、基底の他のベクトルは勾配に共役である。そこで、この方法を'''共役勾配法'''と呼ぶ<ref name="mori"/><ref name="hpc"/><ref name="clang"/>。 |
|||
'''r'''<sub>''k''</sub>を''k''ステップ目での[[残差]] |
|||
{{Indent|<math> \mathbf{r}_k = \mathbf{b} - \mathbf{Ax}_k </math>}} |
|||
とする。'''r'''<sub>''k''</sub>は'''x''' = '''x'''<sub>''k''</sub>での''f''の負の勾配であることに注意されたい。[[最急降下法]]は'''r'''<sub>''k''</sub>の方向に進む解法である。'''p'''<sub>''k''</sub>は互いに共役でなければならないので、'''r'''<sub>''k''</sub>に最も近い方向を共役性を満たすように取る。これは |
|||
{{Indent|<math> \mathbf{p}_{k+1} = \mathbf{r}_{k+1} - \frac{\mathbf{p}_k^{\mathrm{T}} \mathbf{A} \mathbf{r}_{k+1}}{\mathbf{p}_k^{\mathrm{T}}\mathbf{A} \mathbf{p}_k} \mathbf{p}_k </math>}} |
|||
のように表すことができる(記事冒頭の図を参照)。 |
|||
===アルゴリズム=== |
|||
以上の方法を簡素化することにより、'''A'''が実対称正定値である場合に'''Ax''' = '''b'''を解くための以下のアルゴリズムを得る<ref name="clang"/>。初期ベクトル'''x'''<sub>0</sub>は近似解もしくは0とする。 |
|||
<math>r_0 = b - A x_0</math> |
|||
<math>p_0 = r_0</math> |
|||
'''for''' (k = 0; ; k++) |
|||
<math>\alpha_k = \frac{r_k^{\rm T} p_k}{p_k^{\rm T} A p_k}</math> |
|||
<math>x_{k+1} = x_k + \alpha_k p_k</math> |
|||
<math>r_{k+1} = r_k - \alpha_k A p_k</math> |
|||
'''if''' <math>r_{k + 1}</math> が十分に小さい '''then''' |
|||
'''break''' |
|||
<math>\beta_k = \frac{r_{k+1}^{\rm T} r_{k+1}}{r_k^{\rm T} r_k}</math> |
|||
<math>p_{k+1} = r_{k+1} + \beta_k p_k</math> |
|||
結果は <math>x_{k+1}</math> |
|||
=== Octaveでの共役勾配法の記述例=== |
|||
[[Gnu Octave]]で書くと以下のようになる。 |
|||
<pre> |
|||
function [x] = conjgrad(A,b,x0) |
|||
r = b - A*x0; |
|||
w = -r; |
|||
z = A*w; |
|||
a = (r'*w)/(w'*z); |
|||
x = x0 + a*w; |
|||
B = 0; |
|||
for i = 1:size(A)(1); |
|||
r = r - a*z; |
|||
if( norm(r) < 1e-10 ) |
|||
break; |
|||
endif |
|||
B = (r'*z)/(w'*z); |
|||
w = -r + B*w; |
|||
z = A*w; |
|||
a = (r'*w)/(w'*z); |
|||
x = x + a*w; |
|||
end |
|||
end |
|||
</pre> |
|||
===前処理=== |
|||
[[前処理行列]]とは、'''A'''と同値な'''P'''<sup>-1</sup>'''A''' ('''P'''<sup>T</sup>)<sup>-1</sup>の[[条件数]]が'''A'''より小さく、'''Ax'''='''b'''より'''P'''<sup>-1</sup>'''A''' ('''P'''<sup>T</sup>)<sup>-1</sup> '''x'''′ ='''P'''<sup>-1</sup>'''b'''′の方が容易に解けるような正定値行列 '''P'''.'''P'''<sup>T</sup>を指す<ref name="clang"/>。前処理行列の生成には、[[ヤコビ法]]、[[ガウス・ザイデル法]]、対称[[SOR法]]などが用いられる<ref>Eisenstat, S. C. (1981). Efficient implementation of a class of preconditioned conjugate gradient methods. SIAM Journal on Scientific and Statistical Computing, 2(1), 1-4.</ref><ref>Kaasschieter, E. F. (1988). Preconditioned conjugate gradients for solving singular systems. Journal of Computational and Applied Mathematics, 24(1-2), 265-275.</ref>。 |
|||
最も単純な前処理行列は、'''A'''の対角要素のみからなる対角行列である。これはヤコビ前処理または対角スケーリングとして知られている。対角行列は逆行列の計算が容易かつメモリも消費しない点で、入門用として優れた方法である。より洗練された方法では、κ('''A''')の減少による収束の高速化と'''P'''<sup>-1</sup>の計算に要する時間とのトレードオフを考えることになる。 |
|||
==正規方程式に対する共役勾配法== |
|||
任意の実行列'''A'''に対して'''A'''<sup>T</sup>'''A'''は対称(半)正定値となるので、係数行列を'''A'''<sup>T</sup>'''A'''、右辺を'''A'''<sup>T</sup>'''b'''とする[[最小二乗法|正規方程式]]を解くことにより、共役勾配法を任意の''n''×''m''行列に対して適用することができる(CGNR法<ref>Black, Noel and Moore, Shirley. "Conjugate Gradient Method on the Normal Equations." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. {{URL|https://mathworld.wolfram.com/ConjugateGradientMethodontheNormalEquations.html}}</ref>)。 |
|||
{{Indent|'''A'''<sup>T</sup>'''Ax''' <nowiki>=</nowiki> '''A'''<sup>T</sup>'''b'''}} |
|||
反復法としては、'''A'''<sup>T</sup>'''A'''を明示的に保持する必要がなく、行列ベクトル積、転置行列ベクトル積を計算すればよいので、''A''が疎行列である場合にはCGNR法は特に有効である。ただし、条件数κ('''A'''<sup>T</sup>'''A''')がκ('''A'''<sup>2</sup>)に等しいことから収束は遅くなる傾向があり、[[前処理行列]]を使用するCGLS (Conjugate Gradient Least Squares<ref>Bjorck, A. (1996). Numerical methods for least squares problems (Vol. 51). SIAM.</ref>)、LSQRなどの解法が提案されている。LSQRは'''A'''が悪条件である場合に最も数値的に安定な解法である<ref>Paige, C. and Saunders, M. "LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares." ACM Trans. Math. Soft. 8, 43-71, 1982.</ref><ref>Paige, C. C., & Saunders, M. A. (1982). Algorithm 583: LSQR: Sparse linear equations and least squares problems. ACM Transactions on Mathematical Software (TOMS), 8(2), 195-209.</ref>。 |
|||
==関連項目== |
|||
*[[双共役勾配法]] (BICG) |
|||
*[[非線形共役勾配法]] |
|||
==脚注== |
|||
{{脚注ヘルプ}} |
|||
=== 出典 === |
|||
{{reflist|2}} |
|||
==参考文献== |
|||
{{Refbegin|2}} |
|||
*{{cite journal|last = Hestenes|first = Magnus R.|coauthors = Stiefel, Eduard|title = Methods of Conjugate Gradients for Solving Linear Systems|journal = Journal of Research of the National Bureau of Standards|volume = 49|issue = 6|date =1952-12|url = http://nvl.nist.gov/pub/nistpubs/jres/049/6/V49.N06.A08.pdf}} |
|||
*{{Cite Book|first = Kendell A. |last =Atkinson |date =1988 |title =An introduction to numerical analysis |edition=2nd |chapter=Section 8.9 |publisher=John Wiley and Sons |isbn= 0-471-50023-2 }} |
|||
* {{Cite Book|first =Mordecai |last =Avriel |date =2003 |title=Nonlinear Programming: Analysis and Methods. |publisher= Dover Publishing. |isbn=0-486-43227-0 }} |
|||
* {{Cite Book|first =Gene H. |last =Golub |first2 =Charles F. |last2=Van Loan |date=1996 |title =Matrix computations |edition=2nd |chapter=Chapter 10 |publisher=Johns Hopkins University Press. |isbn=0-8018-5414-8 }} |
|||
* {{Cite Book|first =Gerard | last =Meurant |first2 =Petr | last2 =Tichy | date=2024|title =Error Norm Estimation in the Conjugate Gradient Algorithm |publisher=SIAM | isbn= 978-1-61197-785-1}} |
|||
{{Refend}} |
|||
==外部リンク== |
|||
*[http://www.math-linux.com/spip.php?article54 Conjugate Gradient Method] by Nadir Soualem. |
|||
*[http://www.math-linux.com/spip.php?article55 Preconditioned conjugate gradient method] by Nadir Soualem. |
|||
*[https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf An Introduction to the Conjugate Gradient Method Without the Agonizing Pain] by Jonathan Richard Shewchuk. |
|||
*[http://www-users.cs.umn.edu/~saad/books.html Iterative methods for sparse linear systems] by Yousef Saad |
|||
*[http://www.stanford.edu/group/SOL/software/lsqr.html LSQR: Sparse Equations and Least Squares] by Christopher Paige and Michael Saunders. |
|||
{{linear algebra}} |
|||
{{最適化アルゴリズム}} |
|||
{{authority control}} |
|||
{{DEFAULTSORT:きようやくこうはいほう}} |
|||
[[Category:最適化アルゴリズム]] |
|||
[[Category:数値線形代数]] |
|||
[[Category:数学に関する記事]] |
|||
[[Category:勾配法]] |
|||
2024年11月27日 (水) 11:52時点における最新版
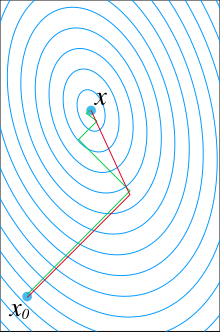
共役勾配法(きょうやくこうばいほう、英: conjugate gradient method、CG法とも呼ばれる)は対称正定値行列を係数とする連立一次方程式を解くためのアルゴリズムである[1][2][3][4]。反復法として利用され[1][2][3][4]、コレスキー分解のような直接法では大きすぎて取り扱えない、大規模な疎行列を解くために利用される。そのような問題は偏微分方程式などを数値的に解く際に常に現れる[1][5][6][7]。
共役勾配法は、エネルギー最小化などの最適化問題を解くために用いることもできる[8][9][10]。
双共役勾配法は、共役勾配法の非対称問題への拡張である[11]。また、非線形問題を解くために、さまざまな非線形共役勾配法が提案されている[12][13][14]。
詳説
[編集]対称正定値行列Aを係数とするn元連立一次方程式
Ax = b
の解をx*とする。
直接法としての共役勾配法
[編集]非零ベクトルu、vが
を満たすとき、u、vはAに関して共役であるという[2][3][4]。Aは対称正定値なので、左辺から内積
を定義することができる。この内積に関して2つのベクトルが直交するなら、それらのベクトルは互いに共役である。 この関係は対称で、uがvに対して共役なら、vもuに対して共役である(この場合の「共役」は複素共役と無関係であることに注意)。
{pk}をn個の互いに共役なベクトル列とする。pkは基底Rnを構成するので、Ax = bの解x*をこの基底で展開すると、
と書ける。ただし係数は
で与えられる。
この結果は、上で定義した内積を考えるのが最も分かりやすいと思われる。
以上から、Ax = bを解くための方法が得られる。すなわち、まずn個の共役な方向を見つけ、それから係数αkを計算すればよい。
反復法としての共役勾配法
[編集]共役なベクトル列pkを注意深く選ぶことにより、一部のベクトルからx*の良い近似を得られる可能性がある。そこで、共役勾配法を反復法として利用することを考える[2][3][4]。こうすることで、nが非常に大きく、直接法では解くのに時間がかかりすぎるような問題にも適用することができる。
x*の初期値をx0 = 0 とする。x*が二次形式
を最小化する一意な解であることに注意し、最初の基底ベクトルp1をx = x0でのfの勾配Ax0−b=−bとなるように取る。このとき、基底の他のベクトルは勾配に共役である。そこで、この方法を共役勾配法と呼ぶ[2][3][4]。
rkをkステップ目での残差
とする。rkはx = xkでのfの負の勾配であることに注意されたい。最急降下法はrkの方向に進む解法である。pkは互いに共役でなければならないので、rkに最も近い方向を共役性を満たすように取る。これは
のように表すことができる(記事冒頭の図を参照)。
アルゴリズム
[編集]以上の方法を簡素化することにより、Aが実対称正定値である場合にAx = bを解くための以下のアルゴリズムを得る[4]。初期ベクトルx0は近似解もしくは0とする。
for (k = 0; ; k++) if が十分に小さい then break 結果は
Octaveでの共役勾配法の記述例
[編集]Gnu Octaveで書くと以下のようになる。
function [x] = conjgrad(A,b,x0)
r = b - A*x0;
w = -r;
z = A*w;
a = (r'*w)/(w'*z);
x = x0 + a*w;
B = 0;
for i = 1:size(A)(1);
r = r - a*z;
if( norm(r) < 1e-10 )
break;
endif
B = (r'*z)/(w'*z);
w = -r + B*w;
z = A*w;
a = (r'*w)/(w'*z);
x = x + a*w;
end
end
前処理
[編集]前処理行列とは、Aと同値なP-1A (PT)-1の条件数がAより小さく、Ax=bよりP-1A (PT)-1 x′ =P-1b′の方が容易に解けるような正定値行列 P.PTを指す[4]。前処理行列の生成には、ヤコビ法、ガウス・ザイデル法、対称SOR法などが用いられる[15][16]。
最も単純な前処理行列は、Aの対角要素のみからなる対角行列である。これはヤコビ前処理または対角スケーリングとして知られている。対角行列は逆行列の計算が容易かつメモリも消費しない点で、入門用として優れた方法である。より洗練された方法では、κ(A)の減少による収束の高速化とP-1の計算に要する時間とのトレードオフを考えることになる。
正規方程式に対する共役勾配法
[編集]任意の実行列Aに対してATAは対称(半)正定値となるので、係数行列をATA、右辺をATbとする正規方程式を解くことにより、共役勾配法を任意のn×m行列に対して適用することができる(CGNR法[17])。
ATAx = ATb
反復法としては、ATAを明示的に保持する必要がなく、行列ベクトル積、転置行列ベクトル積を計算すればよいので、Aが疎行列である場合にはCGNR法は特に有効である。ただし、条件数κ(ATA)がκ(A2)に等しいことから収束は遅くなる傾向があり、前処理行列を使用するCGLS (Conjugate Gradient Least Squares[18])、LSQRなどの解法が提案されている。LSQRはAが悪条件である場合に最も数値的に安定な解法である[19][20]。
関連項目
[編集]脚注
[編集]出典
[編集]- ^ a b c 山本哲朗『数値解析入門』(増訂版)サイエンス社〈サイエンスライブラリ 現代数学への入門 14〉、2003年6月。ISBN 4-7819-1038-6。
- ^ a b c d e 森正武. 数値解析 第2版. 共立出版.
- ^ a b c d e 数値線形代数の数理とHPC, 櫻井鉄也, 松尾宇泰, 片桐孝洋編(シリーズ応用数理 / 日本応用数理学会監修, 第6巻)共立出版, 2018.8
- ^ a b c d e f g 皆本晃弥. (2005). UNIX & Informatioin Science-5 C 言語による数値計算入門.
- ^ 田端正久; 偏微分方程式の数値解析, 2010. 岩波書店.
- ^ 登坂宣好, & 大西和榮. (2003). 偏微分方程式の数値シミュレーション. 東京大学出版会.
- ^ Zworski, M. (2002). Numerical linear algebra and solvability of partial differential equations. Communications in mathematical physics, 229(2), 293-307.
- ^ Gill, P. E., Murray, W., & Wright, M. H. (1991). Numerical linear algebra and optimization (Vol. 1, p. 74). Redwood City, CA: Addison-Wesley.
- ^ Gilbert, J. C., & Nocedal, J. (1992). Global convergence properties of conjugate gradient methods for optimization. SIAM Journal on optimization, 2(1), 21-42.
- ^ Steihaug, T. (1983). The conjugate gradient method and trust regions in large scale optimization. SIAM Journal on Numerical Analysis, 20(3), 626-637.
- ^ Black, Noel and Moore, Shirley. "Biconjugate Gradient Method." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. mathworld
.wolfram .com /BiconjugateGradientMethod .html - ^ Dai, Y. H. (2010). Nonlinear conjugate gradient methods. Wiley Encyclopedia of Operations Research and Management Science.
- ^ Hager, W. W., & Zhang, H. (2006). A survey of nonlinear conjugate gradient methods. Pacific journal of Optimization, 2(1), 35-58.
- ^ Dai, Y., Han, J., Liu, G., Sun, D., Yin, H., & Yuan, Y. X. (2000). Convergence properties of nonlinear conjugate gradient methods. SIAM Journal on Optimization, 10(2), 345-358.
- ^ Eisenstat, S. C. (1981). Efficient implementation of a class of preconditioned conjugate gradient methods. SIAM Journal on Scientific and Statistical Computing, 2(1), 1-4.
- ^ Kaasschieter, E. F. (1988). Preconditioned conjugate gradients for solving singular systems. Journal of Computational and Applied Mathematics, 24(1-2), 265-275.
- ^ Black, Noel and Moore, Shirley. "Conjugate Gradient Method on the Normal Equations." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. mathworld
.wolfram .com /ConjugateGradientMethodontheNormalEquations .html - ^ Bjorck, A. (1996). Numerical methods for least squares problems (Vol. 51). SIAM.
- ^ Paige, C. and Saunders, M. "LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares." ACM Trans. Math. Soft. 8, 43-71, 1982.
- ^ Paige, C. C., & Saunders, M. A. (1982). Algorithm 583: LSQR: Sparse linear equations and least squares problems. ACM Transactions on Mathematical Software (TOMS), 8(2), 195-209.
参考文献
[編集]- Hestenes, Magnus R.; Stiefel, Eduard (1952-12). “Methods of Conjugate Gradients for Solving Linear Systems”. Journal of Research of the National Bureau of Standards 49 (6).
- Atkinson, Kendell A. (1988). “Section 8.9”. An introduction to numerical analysis (2nd ed.). John Wiley and Sons. ISBN 0-471-50023-2
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods.. Dover Publishing.. ISBN 0-486-43227-0
- Golub, Gene H.; Van Loan, Charles F. (1996). “Chapter 10”. Matrix computations (2nd ed.). Johns Hopkins University Press.. ISBN 0-8018-5414-8
- Meurant, Gerard; Tichy, Petr (2024). Error Norm Estimation in the Conjugate Gradient Algorithm. SIAM. ISBN 978-1-61197-785-1
外部リンク
[編集]- Conjugate Gradient Method by Nadir Soualem.
- Preconditioned conjugate gradient method by Nadir Soualem.
- An Introduction to the Conjugate Gradient Method Without the Agonizing Pain by Jonathan Richard Shewchuk.
- Iterative methods for sparse linear systems by Yousef Saad
- LSQR: Sparse Equations and Least Squares by Christopher Paige and Michael Saunders.



















