「方べきの定理」の版間の差分
表示
削除された内容 追加された内容
PuzzleBachelor (会話 | 投稿記録) m 114.179.121.123 (会話) による ID:72364373 の版を取り消し タグ: 取り消し |
編集の要約なし |
||
| 4行目: | 4行目: | ||
== 内容 == |
== 内容 == |
||
{| |
{| |
||
|[[image:houbeki 001.svg|thumb|200px|図1]] |
|[[image:houbeki 001.svg|thumb|200px|図1 {{ill2|交弦定理|label=弦弦定理|en|Intersecting chords theorem}}]] |
||
|[[image:houbeki 003.svg|thumb|200px|図2]] |
|[[image:houbeki 003.svg|thumb|200px|図2 {{ill2|交割線定理|label=割割定理|en|Intersecting secants theorem}}]] |
||
|[[image:houbeki 005.svg|thumb|200px|図3]] |
|[[image:houbeki 005.svg|thumb|200px|図3 {{ill2|接線割線定理|label=接割定理|en|Tangent-secant theorem}}]] |
||
|} |
|} |
||
[[円 (数学)|円]]O とその[[円周]]上にない[[点]]P を取り、点P を通る2本の[[割線]](円との[[共有点]]が2個の[[直線]])と円O の[[交点]]を A, B と C, D とすると、(図1、図2) |
[[円 (数学)|円]]O とその[[円周]]上にない[[点]]P を取り、点P を通る2本の[[割線]](円との[[共有点]]が2個の[[直線]])と円O の[[交点]]を A, B と C, D とすると、(図1、図2) |
||
2019年6月14日 (金) 09:40時点における版
方べきの定理(方冪の定理、ほうべきのていり)は、平面初等幾何学の定理の1つである。
内容
 |
 |
 |
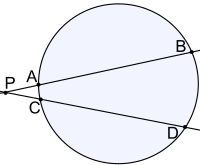
円O とその円周上にない点P を取り、点P を通る2本の割線(円との共有点が2個の直線)と円O の交点を A, B と C, D とすると、(図1、図2)
が成り立つ。
また、P が円O の外側にあるとき、一方の割線が円O の接線となる場合にも、円と割線の交点を A, B、接点を T とすると、(図3)
が成り立つ。
証明
| P が円O の内側にある場合 | 
|
左の図において、同一の弧に対する円周角は互いに等しいから
このことにより、二角相等で
よって
ゆえに
|
| P が円O の外側にある場合 | 
|
左の図において、円に内接する四角形の外角の大きさは、その内対角の大きさに等しいから、
二角相等で
よって
ゆえに
|
| 一方の割線が接線になる場合 | 
|
左の図において、接弦定理により、
また、共通の角で
二角相等で
よって
ゆえに
|


