「ミルズの構造化プログラミング」の版間の差分
I.hidekazu (会話 | 投稿記録) m編集の要約なし |
m編集の要約なし |
||
| 1行目: | 1行目: | ||
{{独自研究|date=2022年4月}} |
|||
[[Image:Stepwise-refinement in structured programming.png|thumb|360px|「構造化プログラミング」によって制御フローのジャングルが整理され、“うまく”構造化された流れ図]] |
[[Image:Stepwise-refinement in structured programming.png|thumb|360px|「構造化プログラミング」によって制御フローのジャングルが整理され、“うまく”構造化された流れ図]] |
||
'''ミルズの構造化プログラミング'''(ミルズのこうぞうかプログラミング、{{lang-en-short|Mills' structured programming}})とは、ソフトウェアの複雑な制御フローを連接・選択・繰り返しおよび'''ネスティング'''(nesting)の多層化<ref>このネストの反復によって構成される多層的な「構造」が構造化プログラミングの言う「良い構造」である。</ref>によって整理しながらプログラミングを行う[[段階的詳細化法]]を言う<ref>[[#河村(1995)|河村(1995)]]pp.112-113、H.D.Mills, R.C.Linger, a.R.Hevner, “ボックス構造化情報システム” p.1(p.187) {{cite book | 和書 | title=ソフトウェアエンジニアリング論文集80's | editor=Tom DeMarco, Timothy Lister(編著) | editor2=児玉公信(監訳) | publisher=翔泳社 | year=2006 | pages=pp.187-219}}収録</ref>。 |
'''ミルズの構造化プログラミング'''(ミルズのこうぞうかプログラミング、{{lang-en-short|Mills' structured programming}})とは、ソフトウェアの複雑な制御フローを連接・選択・繰り返しおよび'''ネスティング'''(nesting)の多層化<ref>このネストの反復によって構成される多層的な「構造」が構造化プログラミングの言う「良い構造」である。</ref>によって整理しながらプログラミングを行う[[段階的詳細化法]]を言う<ref>[[#河村(1995)|河村(1995)]]pp.112-113、H.D.Mills, R.C.Linger, a.R.Hevner, “ボックス構造化情報システム” p.1(p.187) {{cite book | 和書 | title=ソフトウェアエンジニアリング論文集80's | editor=Tom DeMarco, Timothy Lister(編著) | editor2=児玉公信(監訳) | publisher=翔泳社 | year=2006 | pages=pp.187-219}}収録</ref>。 |
||
| 18行目: | 19行目: | ||
各制御処理を順次プログラムに限定してしまえば、そのソフトウェアの設計におけるフローチャートは上から下に読めるものとなり、文書を読むように人間の思考の流れとプログラムの進行の流れとが一致することになる。さらにその構成要素の順次プログラムは、'''経験的に'''<ref>任意の制御構造をもつ順次プログラムがこの3種類の基本制御構造を組み合わせることで実現できるということを主張する構造化定理(structured theorem)は、ダイクストラらが構造化プログラミングを提唱した1972年の7年後の1979年にRichard C. Linger, Bernard I. Witt, H. D. Millsの共著本によって示された。[https://dl.acm.org/citation.cfm?id=578547 Structured Programming] |
各制御処理を順次プログラムに限定してしまえば、そのソフトウェアの設計におけるフローチャートは上から下に読めるものとなり、文書を読むように人間の思考の流れとプログラムの進行の流れとが一致することになる。さらにその構成要素の順次プログラムは、'''経験的に'''<ref>任意の制御構造をもつ順次プログラムがこの3種類の基本制御構造を組み合わせることで実現できるということを主張する構造化定理(structured theorem)は、ダイクストラらが構造化プログラミングを提唱した1972年の7年後の1979年にRichard C. Linger, Bernard I. Witt, H. D. Millsの共著本によって示された。[https://dl.acm.org/citation.cfm?id=578547 Structured Programming] |
||
</ref>、連接(concatenation)・選択(selection)・繰り返し(repetition)の3種類に分けられるとし、その正しさは、一人の人間が最初の2つに対しては'''数え上げ推論'''(enumaration)、3つめに対しては'''数学的帰納法'''(mathematical induction)<ref>この数学的帰納法を用いる検証については計算機による自動化を行うことができる。[[自動定理証明|定理自動証明]]</ref>を適用することで確認できると主張した<ref>[[#構造化プログラミング(1972)|構造化プログラミング(1972)]]p.22</ref>。 |
</ref>、連接(concatenation)・選択(selection)・繰り返し(repetition)の3種類に分けられるとし、その正しさは、一人の人間が最初の2つに対しては'''数え上げ推論'''(enumaration)、3つめに対しては'''数学的帰納法'''(mathematical induction)<ref>この数学的帰納法を用いる検証については計算機による自動化を行うことができる{{要出典|date=2022年4月}}。[[自動定理証明|定理自動証明]]</ref>を適用することで確認できると主張した<ref>[[#構造化プログラミング(1972)|構造化プログラミング(1972)]]p.22</ref>{{出典無効|date=2022-04-13}}。 |
||
上記道具立てを使用すれば、原理的には大規模ソフトウェアであっても開発することができ、正しさも検証することができる<ref>ここで、順次プログラムの中にgoto文を一行でも入れてしまうと、数え上げ推論による正当性検証ができなくなってしまい、「ソフトウェア全体の正しさ」というものが原理的に定義できなくなってしまうのである。 |
上記道具立てを使用すれば、原理的には大規模ソフトウェアであっても開発することができ、正しさも検証することができる<ref>ここで、順次プログラムの中にgoto文を一行でも入れてしまうと、数え上げ推論による正当性検証ができなくなってしまい、「ソフトウェア全体の正しさ」というものが原理的に定義できなくなってしまうのである。{{矛盾|article=ミルズの構造化プログラミング|section=構造化定理(the structure theorem)|date=2022年4月}} |
||
</ref>。しかしながら、記憶力という人間の能力の限界によってこれを巨大ソフトウェアの全要素に対して実行することは現実的ではない。これを解決する手段としてダイクストラが提案したのが'''抽象'''(abstract)であったが、あまり認知されなかった<ref>ダイクストラが提案したのは次の三つであり、それらを駆使できる構造を持ったプログラム開発が構造化プログラミングであった。 |
</ref>。しかしながら、記憶力という人間の能力の限界によってこれを巨大ソフトウェアの全要素に対して実行することは現実的ではない。これを解決する手段としてダイクストラが提案したのが'''抽象'''(abstract)であったが、あまり認知されなかった<ref>ダイクストラが提案したのは次の三つであり、それらを駆使できる構造を持ったプログラム開発が構造化プログラミングであった。 |
||
;三つの知性の道具 |
;三つの知性の道具 |
||
| 37行目: | 38行目: | ||
== 構造化文(structured statement) == |
== 構造化文(structured statement) == |
||
ダイクストラは、従来のフローチャートの進行方向を単線化するため、プログラムは順次プログラムでなくてはならず、さらにその順次プログラムは'''フローチャートの制御の規律を固守するため'''<ref>[[#構造化プログラミング(1972)|構造化プログラミング(1972)]] p.22<br /> |
ダイクストラは、従来のフローチャートの進行方向を単線化するため、プログラムは順次プログラムでなくてはならず、さらにその順次プログラムは'''フローチャートの制御の規律を固守するため'''<ref>[[#構造化プログラミング(1972)|構造化プログラミング(1972)]] p.22<br /> |
||
すなわち、人間が把握することができるようにするために3つの種類に限定したのである。</ref>、連接(concatenation)・選択(selection)・繰り返し(repetition)の三種類の単位に限定し<ref>ただし、ダイクストラの構造化文の限定の仕方は数学的ではない。[[ペール・マルティン=レーフ]]は自身の[[直観主義型理論]]において、フローチャートの代わりに[[ゲンツェン]]流の自然演繹を拡張したものを採用した上で、正しさを確認できるものとしての構造化文に代わるものとしてカノニカル表現(canonical expression)と呼ばれるものを採用している。 |
すなわち、人間が把握することができるようにするために3つの種類に限定したのである。</ref>、連接(concatenation)・選択(selection)・繰り返し(repetition)の三種類の単位に限定し<ref>ただし、ダイクストラの構造化文の限定の仕方は数学的ではない。[[ペール・マルティン=レーフ]]は自身の[[直観主義型理論]]において、フローチャートの代わりに[[ゲンツェン]]流の自然演繹を拡張したものを採用した{{要出典|date=2022年4月}}上で、正しさを確認できるものとしての構造化文に代わるものとしてカノニカル表現(canonical expression)と呼ばれるものを採用している{{要出典|date=2022年4月}}。 |
||
</ref>、goto文は使用しないようにすべきであるとした<ref>goto文を含むプログラムの正しさを他者に証明して納得させる方法がないからである。</ref>{{#tag:ref|goto文を避けて構造化文を用いるようプログラマーに教えることが、構造化プログラミングの伝統的な知恵である<ref name="sp_in_introductory_programming_courses">C.A.R.Hoare, "Structured programming in introductory programming courses", ''Structured Programming'', Infotech state of the art report, 1976, pp.257-263, Infotech International. </ref>}}。なお、[[ニクラウス・ヴィルト]]はこれらを'''構造化文'''(structured statement)と呼んだ <ref name="systematic_programming">N.ヴィルト, ''系統的プログラミング/入門'', 野下浩平, 筧捷彦, 武市正人 訳, 近代科学社, 1978. </ref> |
</ref>、goto文は使用しないようにすべきであるとした<ref>goto文を含むプログラムの正しさを他者に証明して納得させる方法がないからである{{要出典|date=2022年4月}}。</ref>{{#tag:ref|goto文を避けて構造化文を用いるようプログラマーに教えることが、構造化プログラミングの伝統的な知恵である<ref name="sp_in_introductory_programming_courses">C.A.R.Hoare, "Structured programming in introductory programming courses", ''Structured Programming'', Infotech state of the art report, 1976, pp.257-263, Infotech International. </ref>}}。なお、[[ニクラウス・ヴィルト]]はこれらを'''構造化文'''(structured statement)と呼んだ <ref name="systematic_programming">N.ヴィルト, ''系統的プログラミング/入門'', 野下浩平, 筧捷彦, 武市正人 訳, 近代科学社, 1978. </ref> |
||
<gallery widths="200px" heights="200px" perrow=6 > |
<gallery widths="200px" heights="200px" perrow=6 > |
||
File:Concatenation in structured programming.png |連接(concatenation) |
File:Concatenation in structured programming.png |連接(concatenation) |
||
| 55行目: | 56行目: | ||
:全体のプログラムの証明 = |
:全体のプログラムの証明 = |
||
:「抽象処理Rの詳細レベル0の証明」 × 「抽象処理Rの詳細レベル1の証明」 |
:「抽象処理Rの詳細レベル0の証明」 × 「抽象処理Rの詳細レベル1の証明」 |
||
の二つの証明に分離して実行することができるようになる<ref>これは、計算機の動作機構である電子回路の世界における、回路設計を行う際の[[テブナンの定理|鳳・テブナンの定理]]の役割とほとんど一緒である。</ref>。 |
の二つの証明に分離して実行することができるようになる<ref>これは、計算機の動作機構である電子回路の世界における、回路設計を行う際の[[テブナンの定理|鳳・テブナンの定理]]の役割とほとんど一緒である{{要出典|date=2022年4月}}。</ref>。 |
||
{{-}} |
{{-}} |
||
== 構造化定理(the structure theorem) == |
== 構造化定理(the structure theorem) == |
||
2022年4月13日 (水) 21:10時点における版
この記事には独自研究が含まれているおそれがあります。 |

ミルズの構造化プログラミング(ミルズのこうぞうかプログラミング、英: Mills' structured programming)とは、ソフトウェアの複雑な制御フローを連接・選択・繰り返しおよびネスティング(nesting)の多層化[1]によって整理しながらプログラミングを行う段階的詳細化法を言う[2]。
エドガー・ダイクストラの構造化プログラミングの主張[3]をIBMのハーラン・ミルズ(Harlan D. Mills)が敷衍したもので、構造化定理に基づいて単純にgoto文を使用しないgoto-lessプログラミングと理解されていることが多い[4]。
概要

プログラムの設計手法としてのフローチャート(flow chart; 流れ図)は、歴史的には1947年にHerman Goldstine及びフォン・ノイマンによって導入されたものである[5]。フローチャートの導入は、それまでのほとんど設計をおこなわず直接プログラミングを行う職人芸的手法を改善するものであったが[6]、当時のプログラミング作法を反映して各制御のエリアの記載方法に統一性がなく、一つの入力に対して二つの出力があったり、必ずしも上から下に読めるように定められておらず、小規模ソフトウェアであれば一人の人間の力で把握することはできるものの、大規模なものとなればその把握は実質的に不可能なものであった。
大規模プログラムの開発に関心を持っていた[7]オランダのエドガー・ダイクストラは、仕様通り正しく動く大規模ソフトェア開発の困難さを、この巨大になったときその把握が人間の能力を超えてしまう当時の制御処理方法の無秩序さに求め、ソフトウェア開発において構成要素である各制御処理は、抽象化したとき『頭に一つの入口を持ち尻尾に一つの出口』を持つ順次プログラム(sequential program)に限定すべきと主張した[8][9]。そのため順次プログラムの構成を自動的に破壊してしまうgoto文は害があると主張し論争を巻き起こすこととなった(goto文論争[10])。
各制御処理を順次プログラムに限定してしまえば、そのソフトウェアの設計におけるフローチャートは上から下に読めるものとなり、文書を読むように人間の思考の流れとプログラムの進行の流れとが一致することになる。さらにその構成要素の順次プログラムは、経験的に[11]、連接(concatenation)・選択(selection)・繰り返し(repetition)の3種類に分けられるとし、その正しさは、一人の人間が最初の2つに対しては数え上げ推論(enumaration)、3つめに対しては数学的帰納法(mathematical induction)[12]を適用することで確認できると主張した[13][出典無効]。
上記道具立てを使用すれば、原理的には大規模ソフトウェアであっても開発することができ、正しさも検証することができる[14]。しかしながら、記憶力という人間の能力の限界によってこれを巨大ソフトウェアの全要素に対して実行することは現実的ではない。これを解決する手段としてダイクストラが提案したのが抽象(abstract)であったが、あまり認知されなかった[15]。
IBMのハーラン・ミルズは、上記ダイクストラの構造化プログラミングの考え方を単純に要約するために、ソフトウェアの問題を制御フローの問題と同一視した上で、
試行錯誤のコンピュータプログラミング技術をソフトウェア工学へと変える革命のきっかけとなったのは、Dijkstraの構造化プログラミング(1)の考え方である。構造化プログラミングは、どんどん複雑化するソフトウェアの問題を取り扱うため、20年間以上も食い止められることなく増殖し続けてきた制御フローのジャングルを整理することに成功した。制御フローのジャングルは、どんなに複雑なソフトウェアでも3つの基本的な構造、順次(begin-end)、選択(if-then-else)と反復(while-do)で設計でき、しかもその構造は何重にもネストできる(構造化プログラミングの構造)という驚くべき主張で置き換えられた。 — H.D.Mills, R.C.Linger, a.R.Hevner, “ボックス構造化情報システム(1987)” p.1(p.187) Tom DeMarco, Timothy Lister(編著)、児玉公信(監訳) 編『ソフトウェアエンジニアリング論文集80's』翔泳社、2006年、pp.187-219頁。収録
とダイクストラの構造化プログラミングを解釈し、さらにミルズ独自の要素も加えたソフトウェア開発技法を提唱した[16]。このミルズが中心となって要約・発展させたソフトウェア開発技法をミルズの構造化プログラミング(Mills' structured programming)と呼ぶ。
構造化文(structured statement)
ダイクストラは、従来のフローチャートの進行方向を単線化するため、プログラムは順次プログラムでなくてはならず、さらにその順次プログラムはフローチャートの制御の規律を固守するため[17]、連接(concatenation)・選択(selection)・繰り返し(repetition)の三種類の単位に限定し[18]、goto文は使用しないようにすべきであるとした[19][21]。なお、ニクラウス・ヴィルトはこれらを構造化文(structured statement)と呼んだ [22]
-
連接(concatenation)
-
選択(selection)
-
繰り返し(repetition)
抽象とフローチャートのネスト

たとえ3つの構造化文に限定したとしても、非常に多数の構造化文からなるプログラムに対しては、その規模が人間の能力を超えてしまうものであれば、人間がその挙動の正しさを証明することは困難である。
ダイクストラが知性の道具立てとして提示した抽象(abstraction)はこれを解決するものであり、プログラムを構成する部分のまとまりに対して変数名をつけるように名前をつけることで、正しさを証明すべき箇所を分割する。
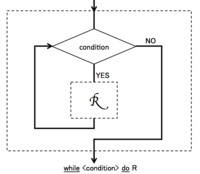
例えば、左図のような多数の連接文を含むwhile文の証明は、知性の道具立ての一つである抽象、すなわちフローチャートのネストをすることで、
- 全体のプログラムの証明 =
- 「抽象処理Rの詳細レベル0の証明」 × 「抽象処理Rの詳細レベル1の証明」
の二つの証明に分離して実行することができるようになる[23]。
構造化定理(the structure theorem)
ダイクストラのフローチャートに関する提案は、有効に思われたが数学的根拠に乏しかった。代わりにミルズらは、次の構造化定理(the structure theorem)を導入することで、一般的分岐を与える命令(GOTO文)の除去の正当化を行った。
- 構造化定理(the structure theorem)[24]
- 任意の固有プログラム(proper program)は、元プログラムの関数と述語それに代入と付加したカウンターによるテストを用いると、{順次(sequence)、選択(ifthenelse)、繰り返し(whiledo)}を基本セットとする構造化プログラムと等価な関数となる。
証明の概要
証明にあたって肝心な部分は、プログラムの制御フローの全てを単一のグローバルな while ループに置き換え、プログラム全体を常に走査できるようにするところにある。さらに、行番号やラベルに代わってプログラムカウンターと呼ばれる呼び出し位置を指定する変数を付け加えることでgoto文と同等の機能をwhiledoとifthenelseで提供することができる。
{変換前goto文}
program main(input, output);
label 10, 20, 30, 40;
begin
10: writeln('step 1'); goto 30;
20: writeln('step 2'); goto 40;
30: writeln('step 3'); goto 20;
40:
end.
このプログラムを変換すると以下のようにgoto文無しに書くことができる。
{変換後}
program main(input, output);
var pcnter : integer; {プログラムカウンター}
begin
pcnter := 10;
while pcnter > 0 do
begin
if pcnter = 10 then begin writeln('step 1'); pcnter := 30; end;
if pcnter = 20 then begin writeln('step 2'); pcnter := 40; end;
if pcnter = 30 then begin writeln('step 3'); pcnter := 20; end;
if pcnter = 40 then pcnter := -1; {プログラムカウンターに-1が代入されたらwhiledoから脱出する。}
end;
end.
脚注
- ^ このネストの反復によって構成される多層的な「構造」が構造化プログラミングの言う「良い構造」である。
- ^ 河村(1995)pp.112-113、H.D.Mills, R.C.Linger, a.R.Hevner, “ボックス構造化情報システム” p.1(p.187) Tom DeMarco, Timothy Lister(編著)、児玉公信(監訳) 編『ソフトウェアエンジニアリング論文集80's』翔泳社、2006年、pp.187-219頁。収録
- ^ 構造化プログラミング(1972)
- ^ ただし、次のような批判がある。
- [2]の表題にあるstructured programming(構造化プログラミング)ということばは、(ダイクストラ)氏の細心かつ厳格なライフスタイルを表現するものとして言い出されたが、のちにIBM社の誇る、Dijkstra教授とはまったく別種の天才 Harlan D.Mills氏によってまったくちがう意味に転用された。プログラマー(職業としてではなく職種としての)に if ... や if ... else ... や while ... だけを使用させ、gotoの使用を禁止すれば、ダメな連中でも少しはましなプログラムを書いてくるだろう、とういうのである。これもまた実におもしろい発想で、広く影響を及ぼしたが、内容はDijkstra流とはほとんど無関係と言ってよい。
- 木村泉,米澤明憲『算法表現論』 12巻、岩波書店〈岩波講座 情報科学〉、1982年。 pp.57-58
- [2]の表題にあるstructured programming(構造化プログラミング)ということばは、(ダイクストラ)氏の細心かつ厳格なライフスタイルを表現するものとして言い出されたが、のちにIBM社の誇る、Dijkstra教授とはまったく別種の天才 Harlan D.Mills氏によってまったくちがう意味に転用された。プログラマー(職業としてではなく職種としての)に if ... や if ... else ... や while ... だけを使用させ、gotoの使用を禁止すれば、ダメな連中でも少しはましなプログラムを書いてくるだろう、とういうのである。これもまた実におもしろい発想で、広く影響を及ぼしたが、内容はDijkstra流とはほとんど無関係と言ってよい。
- ^ Herman H. Goldstine, John von Neuman (1947), Planning and coding of problems for an electronic computing instrument
- ^ 河村(1995) p.112
- ^ 構造化プログラミング(1972)p.2
- ^ ダイクストラは作法としてプログラムは順次プログラムであるように記述するべきとしただけで、プログラミング言語に構文論的制約をつけるかどうかについては述べていない。順次プログラムはちょうど数学における"関数"(function)とみることもできることから、構造化プログラミングは関数型プログラミングと親和性が高い。
- ^ ミルズはこれを順次プログラムではなく固有プログラム(proper program)と呼んだ。
- ^ 論争だけが取り上げられた結果、goto-lessプログラミングやtop-downプログラミングは構造化プログラミングと同一視されることとなってしまった。筧, 捷彦 (1975). “ストラクチャード・プログラミング用言語”. 情報処理 (情報処理学会) 16 (10): 856-863. NAID 110002720279.。
- ^ 任意の制御構造をもつ順次プログラムがこの3種類の基本制御構造を組み合わせることで実現できるということを主張する構造化定理(structured theorem)は、ダイクストラらが構造化プログラミングを提唱した1972年の7年後の1979年にRichard C. Linger, Bernard I. Witt, H. D. Millsの共著本によって示された。Structured Programming
- ^ この数学的帰納法を用いる検証については計算機による自動化を行うことができる[要出典]。定理自動証明
- ^ 構造化プログラミング(1972)p.22
- ^ ここで、順次プログラムの中にgoto文を一行でも入れてしまうと、数え上げ推論による正当性検証ができなくなってしまい、「ソフトウェア全体の正しさ」というものが原理的に定義できなくなってしまうのである。[矛盾]
- ^ ダイクストラが提案したのは次の三つであり、それらを駆使できる構造を持ったプログラム開発が構造化プログラミングであった。
- 三つの知性の道具
- 数え上げ推論(enumeration):一人の人間の能力でできる範囲でプログラムの命令の妥当性を一つ一つ確認すること
- 数学的帰納法(mathematical induction):while文など計算機特有の繰り返し文についてのみ数学的帰納法を用いて確認すること
- 抽象(abstraction):処理のまとまりに名前をつけた上で詳細化を後回しにし、仮に正しいとしておくこと
- ^ StructuredProgramming(1979)
- ^ 構造化プログラミング(1972) p.22
すなわち、人間が把握することができるようにするために3つの種類に限定したのである。 - ^ ただし、ダイクストラの構造化文の限定の仕方は数学的ではない。ペール・マルティン=レーフは自身の直観主義型理論において、フローチャートの代わりにゲンツェン流の自然演繹を拡張したものを採用した[要出典]上で、正しさを確認できるものとしての構造化文に代わるものとしてカノニカル表現(canonical expression)と呼ばれるものを採用している[要出典]。
- ^ goto文を含むプログラムの正しさを他者に証明して納得させる方法がないからである[要出典]。
- ^ C.A.R.Hoare, "Structured programming in introductory programming courses", Structured Programming, Infotech state of the art report, 1976, pp.257-263, Infotech International.
- ^ goto文を避けて構造化文を用いるようプログラマーに教えることが、構造化プログラミングの伝統的な知恵である[20]
- ^ N.ヴィルト, 系統的プログラミング/入門, 野下浩平, 筧捷彦, 武市正人 訳, 近代科学社, 1978.
- ^ これは、計算機の動作機構である電子回路の世界における、回路設計を行う際の鳳・テブナンの定理の役割とほとんど一緒である[要出典]。
- ^ StructuredProgramming(1979) p.118
参考文献
- E.W.ダイクストラ; C.A.R.ホーア; O.-J.ダール 著、野下浩平 訳『構造化プログラミング』サイエンス社、1975年。
- 河村 一樹『ソフトウェア工学入門』近代科学社、1995年。(改訂版は内容が異なる)
- Richard C. Linger,Harlan D. Mills,Bernard I. Wit (1979). IBM Corporation. ed. Structured Programming: Theory and Practice. Addison-Wesley