「タイル張り」の版間の差分
改名提案 |
|
(相違点なし)
| |
2023年7月19日 (水) 14:33時点における版
平面充填(へいめんじゅうてん)とは、平面内を有限種類の平面図形(タイル)で隙間なく敷き詰める操作である。敷き詰めたタイルからなる平面全体を平面充填形という。
平面敷き詰め、タイル貼り、タイリング (tiling) 、テセレーション (tessellation) ともいう。ただし「平面」を明言しない場合は、曲面充填や、場合によっては2次元以外の空間の充填を含む。広義のテセレーション等については、空間充填を参照。平面充填は広義の空間充填の一種で、2次元ユークリッド空間の充填である。
多面体は多角形による球面充填(曲面充填の一種)と考えることができる。そのため、多角形による平面充填は多面体と共通点が多く、便宜上多面体に含めて論じられることもある。
1種類のタイルによる平面充填
正多角形
1種類で平面を充填できる正多角形は、正三角形、正方形、正六角形の3種類のみであり、ピタゴラスによって証明された。これらは正平面充填形 (Regular Tessellation) とも呼ばれる。
-
正三角形による平面充填
-
正方形による平面充填
-
正六角形による平面充填
正三角形、正方形については、図の充填のほかに、頂点をずらした充填も可能である。ただし、隣のタイルの頂点と接する辺を、2辺が内角180°で接していると考えれば、これらは実際は、後述する、一般の四角形、平行六角形による充填の特殊ケースとなる。
1種類の正多角形による(頂点をずらさない)平面充填は、正多角形同様、シュレーフリ記号 {p, q} (正 p 角形が q 個頂点に集まる)で表せる。
- 正三角形 {3, 6}
- 正方形 {4, 4}
- 正六角形 {6, 3}
正 p 角形の内角を q 倍すると 360° になることから、
である。これから、1種類の正多角形による充填がこの3つしか存在しないことが証明できる。
平行四辺形・任意の三角形
全ての平行四辺形は、1種類で平面充填可能である。また、全ての三角形は、合同なものを2つ組み合わせることで平行四辺形となる。従って、全ての三角形は平面充填可能である。
平行六辺形・任意の四角形
全ての合同な平行六辺形(3組の対辺が平行で等しい六角形)は平面敷き詰め可能である。また、全ての四角形は、合同なものを二つ組み合わせることで平行六辺形となる。従って、全ての四角形は平面敷き詰め可能である。
平行六辺形は、中心を通る直線で合同な2つの五角形に分けられる。このような五角形は平面敷き詰め可能である。
これらの変形
平面充填形に対して、対応する場所に凹凸をつけた場合も敷き詰め可能。
正方形の例:



平行六辺形の例:

多角形
この節の加筆が望まれています。 |
五角形の平面充填は、2015年に新しいパターンが発見され全部で15個となった。(これ以上存在しないことは既に証明されている)

アルキメデスの平面充填の双対
#双対充填を参照。
複数種類のタイルによる平面充填
正多角形
一種類の場合と同じように、正多角形のみでできていて、頂点形状が一様なアルキメデスの平面充填と呼ばれる平面充填が8種類あり、半正多面体の一種とされることもある。括弧中は頂点形状(各頂点に集まる正多角形の種類と順序)を表す。
-
正三角形4枚、正六角形1枚 (3, 3, 3, 3, 6)
-
正三角形3枚、正方形2枚 (3, 3, 3, 4, 4)
-
正三角形3枚、正方形2枚 (3, 3, 4, 3, 4)
-
正三角形1枚、正方形2枚、正六角形1枚 (3, 4, 6, 4)
-
正三角形2枚、正六角形2枚 (3, 6, 3, 6)
-
正三角形1枚、正十二角形2枚 (3, 12, 12)
-
正方形1枚、正六角形1枚、正十二角形1枚 (4, 6, 12)
-
正方形1枚、正八角形2枚 (4, 8, 8)
ペンローズ・タイル
充填の双対
多角形(特に正多角形)による平面充填には、多面体に対する双対多面体のように、双対を考えることが可能である。
1種類の正多角形による平面充填の双対は次のとおり。シュレーフリ記号の数値が入れ替わっている。
- 正方形 {4, 4} ⇔ 正方形 {4, 4}
- 正三角形 {3, 6} ⇔ 正六角形 {6, 3}
アルキメデスの平面充填の双対は、1種類の(鏡像は同じと考える)多角形による充填となる。
特殊な充填
非周期充填
周期的なパターンによる充填以外に、非周期な充填も可能である。ただし、周期充填の非周期な変形による充填(場所によってランダムな方法でタイルを分割するなど)は、非周期とは考えない。
最初の非周期充填は、1966年に発見された、20426種類のタイルを使う充填である。
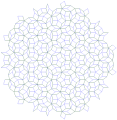
現在最もタイルの種類が少ない非周期充填は、Socolar–Taylor tileと呼ばれる一種類の非連結なタイルによるものである。連結なものに限ればイギリスの物理学者ロジャー・ペンローズが1970年代に考案した、2種の菱形タイル「ペンローズ・タイル」によるものが長らく最小であったが、2023年に帽子の形をした13角形のタイル1種類で可能であることをSmithらが発表した[1][2][3]。
ちなみに高次元では1種類のブロックによる3次元空間の非周期充填が1993年に発見されている。
-
ペンローズタイル。有名な非周期充填。
-
Smithらの“帽子”による非周期充填
中心のある充填

以上は、平面のあらゆる部分が同等な充填であったが、そうでない充填もある。平面上に中心を定め、そこから放射状にタイルを敷き詰める放射充填 (radial tiling) や、螺旋状にタイルを敷き詰める螺旋充填 (spiral tiling) である。
放射充填は、中心を通る放射状の直線で平面を楔形に分割し、そのそれぞれを三角形タイルで充填したものの変形である。直線の1つについて、その両側をタイル1つ分だけずらせば、螺旋充填となる。一見、複雑に見えるが、回転対称性などの対称性を持つ周期充填である。
アインシュタイン問題

アインシュタイン問題とは、繰り返しパターンを形成せずに表面を隙間なく埋めれるタイルは存在するのかどうかという問題である[4]。
2023年、そういうタイルが研究者らによって発見された。そのタイルは14角形であり、「Spectre」と名付けられた[4]。
建築
歴史
この節の加筆が望まれています。 |
出典
- ^ David Smith; Joseph Samuel Myers; Craig S. Kaplan; Chaim Goodman-Strauss (2023), An aperiodic monotile 2023年4月5日閲覧。
- ^ David Smith; Joseph Samuel Myers; Craig S. Kaplan; Chaim Goodman-Strauss (2023), An aperiodic monotile, arXiv:https://arxiv.org/abs/2303.10798
- ^ masapoco (2023年3月29日). “ついに同じパターンを繰り返さず無限に敷き詰められる単一の形状が発見された”. TEXAL. 2024年4月5日閲覧。
- ^ a b “数学の未解決問題「アインシュタイン問題」を“完全解決”する新図形発見 「The hat」を改良”. ITmedia. 2023年6月7日閲覧。