瞬間中心

瞬間中心（しゅんかんちゅうしん、英: instant centre of rotation）とは、回転運動している剛体を仮想的に延長していったとき、速度ベクトルがゼロになる点として定義される。ただし、観測者は静止しているとし、速度ベクトルは静止した観測者から見た速度とする。もし、観測者や座標系が静止してない場合を考慮して定義を拡張するならば、「速度ベクトルがゼロの点」と定義する代わりに、直感的だが、「もっとも動きが小さい点」と定義しても良い。より直感的な表現で定義を言えば、運動している剛体が、ある瞬間にて、ある点を中心に回転運動を行っていると見なせる場合、その中心点が瞬間中心である。

瞬間中心は物体の外部にあっても内部にあっても良い。剛体が平行直線運動をしている場合には、便宜上、瞬間中心は速度ベクトルに直交する方向の無限遠点に位置すると見なす。

性質

ある瞬間での剛体上のある2点の位置ベクトルおよび速度ベクトルが確定しているときは、この2点の位置から、速度ベクトルの垂直方向へと延長した垂直線の交点に、瞬間中心は存在する。

• 
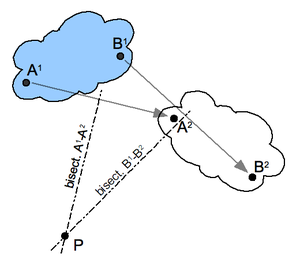
  瞬間中心の例1
  点A₁,B₁が移動して点A₂,B₂へ移った場合、図中の点Pが瞬間中心である。
• 
  瞬間中心の例2
  図中の矢印は速度方向を表している。速度ベクトルの垂直線の交点の点Iが瞬間中心である。

セントロード

各瞬間の瞬間中心の各点をつなぎあわせた軌跡を、セントロード（centroad）という。特に静止した観測者から見た場合のセントロードの軌跡を、固定セントロード（fixed centroad）という。

応用例

この概念は、機構学においてリンク機構の解析などに応用されることが多い。リンク機構への瞬間中心の応用例として、3瞬間中心の定理（ケネディの定理とも言う）などが知られている。

また、生体力学などで関節の運動を扱う際に、回転の中心を「瞬間中心」と呼ぶ場合も、工業力学などで言う場合の瞬間中心と、ほぼ同様の概念である。

他の回転概念との違い

混同しやすい類似の概念として曲率中心や縮閉線などがあるが、これらとは異なる概念である。また、ある点を中心とした公転運動や自転運動の中心点とも区別が必要である。何をして公転の定義や自転の定義とするかにもよるが、一般には、必ずしも公転の中心点または自転の中心点と、瞬間中心が一致するとは限らない。瞬間中心は、あくまでも物体の速度ベクトルの分布を元にして、もっとも動きの小さい点の位置として決定される。

滑らずに転がる円板の瞬間中心

地面との接触点Pが転がる剛体の瞬間中心
転がっている剛体は、地面との接触点を中心にして、自転をしている。

転がる多角形でも、各瞬間での直線との接触点が瞬間中心である。

直線状を滑らずに転がる円板の瞬間中心は、各瞬間での直線と円との接触点になる。剛体の速度ベクトルの分布は図のようになり、そのことから瞬間中心の位置を証明できる。なお、一般に、転がる物体の瞬間中心は、円板にかぎらず楕円形の楕円版でも、あるいは多角形でも、各瞬間での直線との接触点が瞬間中心である。