積分回路(せきぶんかいろ)は、電気回路の一種で入力電圧の波形の時間積分に等しい波形の電圧を出力する回路である。
コンデンサ両端の電圧は、流れ込んだ電流の積分(電荷の総量)に比例するという事実を利用している。
電気回路中を流れる電流というのは、実は荷電粒子(電子など)の移動によって現れる、
電荷の流れである。導体に電流iがt=0からt秒間に渡って流れたとき、
流れ込んで導体を通過した電荷の総量Qは

で与えられる。導体の間に誘電体を挟んだ場合(つまり、コンデンサの場合)、
誘電体中には移動できる自由電子が無いため、
流れ込んだ電流は誘電体の境界面で帯電する。

 はt=0で既に誘電体が帯びていた電荷である。
はt=0で既に誘電体が帯びていた電荷である。
静電誘導によって反対側の境界面にも逆の極性の電荷が帯電するので、
誘電体を挟んで電位差vが生じる。複雑な形状をしていなければ、vはqに比例する。
比例定数をCとすると、

である。
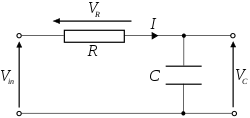 直列RC回路
直列RC回路
ここで、図のようなRC直列回路を考えて、
交流電圧Vを印加する。
初期状態におけるコンデンサCの電荷 とすると、
とすると、
t=0では、オームの法則に従って が流れる。
が流れる。
これが、
コンデンサへ流れ込んでコンデンサに電荷qが蓄えられると、
コンデンサが逆起電力を生じるので、Vの抵抗Rへの分圧が低下し、
回路を流れる電流は小さくなる。
しかし、印加した交流電気の周波数fが十分に大きいならば、
この交流に対してCは短絡とみなせるので、
回路を流れる電流Iは常に で与えられる。
で与えられる。
従って、このときに限り、

である。つまり、RC回路の両端には入力Vの積分の波形をした電圧が現れる。
ミラー積分回路特性計算

より精度の高い積分波形を得るために、オペアンプなど増幅器を用いた回路があり「ミラー積分回路」と呼ばれている。
図中で、アンプが入力インピーダンス無限大の理想的なものであれば、非反転入力端子に出入りする電流は0であるので、抵抗Rを流れる電流と等しい大きさの電流IがコンデンサCに入力端子の方向から流れ込んでくる。オペアンプの非反転入力端子は仮想接地されているので、Rに流れる電流の大きさは である。以上より、
である。以上より、

が成り立っていることが分かる。初期状態において、Cに蓄えられている電荷は既に放電してあるとすると、

であり、入力信号を積分した出力が得られることが分かる。
実際の理想的でないオペアンプでは、入力端子にバイアス電流が流れ込み、また増幅度が有限であるためにまだ誤差を生じ、信号を入力しなくても出力電圧が生じる。元々は真空管で構成した回路で、直線性の良さからオシロスコープの時間軸信号発生回路や、アナログ計算機で、演算増幅器と組んで積分器を構成し主に「微分方程式解析表示器」として製品開発に使われた。
真空管の入力電流はほぼゼロで、コンデンサーの漏洩電流を問題にして選別していたのだが、半導体アンプでは素子が電流制御で、これを防ぐため、電圧制御素子であるFET入力オペアンプを用いたり、入力にバイアス抵抗を繋いで放電させたりしている。時間軸発生など常に初期化される繰り返し型では問題ない。













