籌算

籌算（ちゅうさん、拡張新字体・中: 筹算）とは、算木（中: 筹、算、策^[1]^[2]）と呼ばれる一組の棒を用いる一種の器具代数術。布の盤（算盤）上に算木を並べて行ったことから布算ともいう^[3]。中国のほか朝鮮半島や日本をはじめとする漢字文化圏で広く利用された。

中国において籌算は戦国時代から行われていた。論証的な幾何学を重視する古代ギリシアの数学と比べて、官僚が広大な土地を統治するために必要な実用数学を重んじるのが中国数学の特徴であり、数値計算と代数の分野で特に発達していた^[1]^[3]。その基礎となったのが算木による計算術である。実際、中国文化圏における数学体系の基盤となった『九章算術』（紀元前1世紀ごろ）や類似の数学書は、具体的な問題と籌算による解法という形式で書かれていた^[3]^:53。宋代から元代に至って、朱世傑の4元高次連立方程式に代表される高度な数学が発展したのも籌算の役割が大きかった。しかし13世紀ごろ、実用的な計算をより早く容易に実行できる算盤（そろばん）が普及したことで廃れた。

器具

籌算は基本的に一組の算木と算盤（さんばん）を用いて行われる。『漢書』律暦志では算木を径3 mm、長さ16 cmほどの丸い竹棒だとしている。271本の算木を束にすると、ちょうど手の中に納まるサイズの六角形となるという。また算木は長さや重さの計量に転用されることもあった^[4]^:80。『隋書』律暦志によれば長さ8 cm、幅6 mmの角棒である^[5]。また獣骨製もあり、裕福な商人は象牙と翡翠で作られたものを用いることもあった。算木を並べるための算盤は升目が区切られた布製のものが用いられた（後代は紙製）^[2]^[3]。

1971年、陝西省千陽県で発掘を行っていた中国人の考古学者が、保存状態の良い前漢代（紀元前206年 - 8年）の獣骨製算木が絹袋（籌嚢）に入っているのを発見した^[6]^:47。1975年には竹製の算木が発掘された。前漢より古い時代の算木は発見されていないが、文献資料からは、今から2200年以上前の戦国時代にはすでに籌算法が開花していたことが明らかになっている。

籌算を行うには45項目からなる単純な10進乗算表、すなわち九九表（en:Chinese multiplication table）を覚えていなければならない。中国では春秋時代から九九表は知られており、児童、商人、官僚、数学者らは一様に九九を暗記してきた。

算木数字

数の表示

算木数字は単一の記号（棒）を配置することであらゆる十進数（分数・小数を含む）を表現する唯一の数字表記体系である。1の位に作られた算木数字は、1から5までは1本の縦棒がそれぞれ数1を表す。縦棒が2本なら数2を表し、3本以降も同様である^[7]。6から9までの数を表すには二五進法が用いられ、縦棒の上に置かれた横棒が数5を意味する。下の表に1から9までの数を表す。下段は横棒を基本とした別の表記法である。この表記法は数書『孫子算経』（3 - 5世紀）に解説されていたものである^[4]。

0から9までの算木数字
	0	1	2	3	4	5	6	7	8	9
縦式
横式

			2	3	1
	数231の算木表記
	紛らわしい置き方
	紛らわしい置き方
	棒の向きで桁を表す方法

9より大きい数は十進法によって表される。1の位の左隣に作られた算木数字は、それに10をかけた数を表す。さらに左隣の升は100の位を表し、そこに作られた算木数字は100をかけた数を表す。これ以降も同様である。数231を表すには、右図の上段に示すように、1の位に縦棒を1本置いて1とし、10の位に縦棒を3本置いて30とし、100の位に縦棒を2本置いて200とし、合計して231とする。

籌算は升目のない盤上で行われることが多い。このため、右図の中段のように縦式の算木数字2、3、1を続けて置くと、数231ではなく53や24と間違えられる可能性がある。このような混乱を避けるため、算木数字をいくつか続けて置くときには、右図の最下段に示すように、縦式と横式の表示法を交互に用いる。ただし1の位は必ず縦式とする^[1]^[8]。

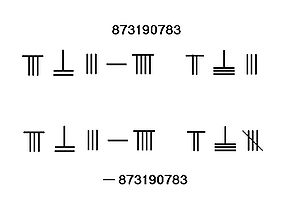
ゼロの表示

算盤上ではアラビア数字のようなゼロ記号は用いられず、升目を空白にすることで数0および位取りのための0を表した^[7]。右図に表された算木数字「873190783」では、1000の位が空白となっている。記号「〇」をゼロの意味で用いる習慣は宋・元のころに始まった^[1]。南宋時代に書かれた『数書九章』が記号「〇」を用いた最古の文献記録である^[4]。

正負の数

世界で初めて負数が導入されたのは中国数学であった^[1]^:20。前漢代の数学者は算木の種類によって正負の数を表していた。赤い算木を正、黒い算木を負とする方法や、断面が三角の算木を正、正方形のものを負とする方法がある^[4]^:101。そのほか、劉徽による『九章算術』の注釈には、右の図のように、最小位に斜めに算木を置くことで負の数を表す方法が記されている^[9]。宋代になると、印刷された数書や筆算で負数を表す場合に赤字や斜線が用いられた^[4]。

小数

『孫子算経』には小数を用いた計量法が記載されている。基本の長さ単位は尺であり、それより小さい単位が以下のように続く。

1尺 = 10 寸

、

1寸 = 10 分

、

1分 = 10 厘

、

1厘 = 10 毛

、

1毛 = 10 糸

、

1糸 = 10 忽

「1尺2寸3分4厘5毛6糸7忽」の長さを算盤上に表すと以下のようになる。

ここではの位が単位長さである尺を表している。

南宋期の数学者秦九韶は長さの計量以外にも小数を適用した。秦の著書『数書九章』では、「1.1446154日」が


日

と表されている。単位の位は下に「日」の字をつけることで示される^[10]。

基本的な計算法

加算

籌算は加法原理と親和性が高い。アラビア数字と異なり、算木数字の各桁を表している棒は加法性を持っている。加算を行うには棒を機械的に動かすだけでよく、1桁の数の加法を暗記する必要はない。これがアラビア数字体系との最大の差異である。たとえば、アラビア数字「1」および「2」を機械的な操作によって「3」へと変換することはできない。

籌算による 3748 + 289 = 4037 の計算手順を以下に示す。

(1)

被加数3748を上段に、加数289を下段に書く。計算は左から右の順で行う。最初に計算するのは下段289の最高位「2」である。

(2)

「2」を表している2本の棒を取り、上の段の「7」に加えて「9」とする。

(3)

下段の「8」を繰り上がらせるため、その真上の「4」から棒を2本移してくる。「8」は繰り上がって「10」となる。

(4)

下段左端の「1」を上段に加えると、「39」が繰り上がって「40」となる。

(5)

下段の「9」を繰り上がらせるため、真上の「8」から棒を1本移してくる。繰り上がって「10」となる。

(6)

下段に残った1本の棒を真上の升に移す。上段に現れた4037が求める和の値である。

この過程により、被加数の棒の配置は適切に変更され、加数からは棒が消えてしまう。

減算

繰り下げなし

繰り下げの必要がない場合、減数（下段）の各桁の棒と同じ数だけ、被減数（上段）の各桁から棒を差し引くだけでいい。上段に残った数が求める差である。下図は減算 54 − 23 = 31 の計算ステップを示している。

(1)

(2)

(3)

繰り下げあり

4231 − 789 = 3442 のように繰り下がりがある場合、より複雑な手順が必要となる。この減算の計算ステップを下に示す。

(1)

被減数4231を上段に、減数789を下段に書く。左から右に計算していく。

(2)

上段1000の位の「4」から1を借り、「3」を残す。借りた1を100の位の「10」とみなし、下段100の位の数「7」を「10」から差し引く。こうして残った3を上段100の位の「2」に加え、「5」とする。下段からも同じく「7」を差し引き、100の位を空白とする。

(3)

上段100の位の「5」から1を借りて「4」を残す。借りた1を10の位の「10」とみなし、下段10の位の数「8」を差し引く。残った2は上段10の位に加えられる。下段10の位も空白とする。

(4)

上段10の位の「5」から1を借りて「4」を残し、借りた1を1の位の「10」とみなして下段の「9」を差し引く。残った1を上段1の位に加える。これで下段のすべての棒が差し引かれたので、上段に残った3442が計算結果となる。

乗算

『孫子算経』には籌算による乗算の方法が詳述されている。下図に 38 × 76 = 2888 の計算ステップを示す。

(1)

被乗数38を上段に、乗数76を下段に書く。乗数の1の位を被乗数の最高位に合わせ、二つの数の間に記録用の余白を空けておく。

(2)

被乗数の最高位から計算を始める（この例では、まず 30 × 76 を、次いで 8 × 76 を計算する）。まず九九の表に基づいて3 × 7 を計算し、答えの21を中段に書く。21の最小桁は乗数10の位の「7」と揃える。

(3)

3 × 6を計算する。答の18を中段に置き、その最小桁を乗数1の位の「6」と揃える（6の上に8を置く）。このとき、21の1の位と、18の10の位が同じ升に入る。

(4)

同じ升に入った棒はすべて合わせて1つの数を作る（中段の数は228となる）。被乗数38のうち「3」の計算は終わったので、棒を取り去る。

(5)

乗数76を1桁ぶん右にずらす（7を横式に、6を縦式に変える）。

(6)

8 × 76 のうち、8 × 7をまず計算する。答の56を中段下の図の位置に書き、その最小桁「6」を今かけた「7」と揃える。「7」の計算はこれで終わったので、升から棒を取り去る。

(7)

下段に残った6を上段の8にかける。その答え48を中段下の図の位置に書き、その最小桁「8」を今かけた「7」に揃える。

(8)

かけ終わった下段の6および上段の8を取り去る。同じ升に入った棒「6」と「4」を合計し、繰り上がった1を隣に加える。ここで中段下の数は608となる。

(9)

中段に現れた二つの数の和を取る。その結果2888が求める積である。

除算

『孫子算経』の方法で除算 309/7 = 441/7 を行う手順を下図に示す。計算は三段に分けて行い、上段から順に「商」、「実（被除数）」、「法（除数）」の名がつけられる^[6]^:49。

(1)

被除数309を中段に、除数7を下段に作る。2つの数は左の桁でそろえておく。上段は空白とする。

			商
			実
			法

(2)

309の「3」は7で割れないので、除数7を1桁ぶん右に動かす（縦式を横式に変える）。

			商
			実
			法

(3)

九九の表に基づいて 30 ÷ 7 を計算し、商4と剰余2を得る。商4を上段に置く。中段から除算が終わった数30を取り除き、剰余2を代わりに書く。

			商
			実
			法

(4)

除数7を1桁分右に動かす（縦式に変える）。

			商
			実
			法

(5)

29 ÷ 7 を計算すると、商は4、剰余1である。商4を上段に書き、このステップで除された29を中段から取り除いて剰余1を代わりに置く。残った数字が求める商44および剰余1を表している。

			商
			実
			法

『孫子算経』の除算アルゴリズムはインドを経由して、825年にアル＝フワーリズミーの手によりそのままの形でイスラム国家に伝えられた。13世紀にはアル＝フワーリズミーの著書がラテン語に翻訳され、孫子の除算法はヨーロッパに広まりガレー算（英語版）へと発展した。925年にアル＝ウクリーディスィー（英語版）が書いた Kitab al-Fusul fi al-Hisab al-Hindi や、11世紀にKushyar ibn Labbanが書いた Principles of Hindu Reckoning にみられる除算法は孫子のアルゴリズムと同じものである。

フワーリズミーの除算法（825年）。

アル＝ウクリーディスィーの除算法（10世紀）。

Kushyar ibn Labbanの除算法（11世紀）。

分数の計算

分数の表記

	$=$	${\frac {1}{7}}$

籌算による除算で、各桁の数を除したときに剰余が出たならば、剰余と除数は上下に並べて置いておかなければならない。劉徽による『九章算術』の注釈では、上の数は「实（実）」、下の数は「法」と呼ばれていた。『孫子算経』では上の数は「子」または「分子」、下の数は「母」または「分母」とされており、現代中国語・日本語の分数用語と同じである。右図の例では、1が分子（剰余）、7が分母（除数）であり、それら2つを合わせて分数 1/7 となる。前節の除算 309/7 の商は 441/7 と読むこともできる。劉徽は『海島算経（中国語版）』において分数を含む計算を多数行った。

このように分子を上に、分母を下に置いて間に水平線を書かない分数の表し方は、除算法と同時にアラビア国家に伝えられた。その使用例は10世紀のアル＝ウクリーディスィーや、15世紀にアル＝カーシーが書いた『算術の鍵』にみられる。

加算

『九章算術』にいう合分術により、分数の加算 1/3 + 2/5 = 11/15 を行う手順を以下に示す^[3]^:21。

(1)

それぞれの分子1と2を算盤の左列に並べ、分母3と5を右列に並べる。

(2)

対角上の2と3をかけ、積6で分子2を置き換える。

(3)

同様に1と5をかけ、積5で分子1を置き換える。

(4)

分母の積 3 × 5 = 15 を取り、右下の5と置き換える。

(5)

分子の和 5 + 6 = 11 を取り、右上の3と置き換える。右側に現れた分数 1115 が求める和である。

減算

『九章算術』にいう減分術により、分数の減算 8/9 − 1/5 = 31/45 を行う手順を以下に示す^[3]^:22。

(1)

それぞれの分子8と1を算盤の左列に並べ、分母9と5を右列に並べる。

(2)

対角線に沿って 1 × 9 = 9 および 5 × 8 = 40 の乗算を行い、分子をそれぞれの積で置き換える。

(3)

分母の積 5 × 9 = 45 を取り、右下の5と置き換える。

(4)

分子の差 40 − 9 = 31 を取り、右上の9と置き換える。右列に現れた 3145 が求める解である。

乗算

『九章算術』にいう大広田術により、帯分数の乗算 31/3 × 52/5 = 18 を行う手順を以下に示す^[3]^:26-27。

(1)

被乗数 313 を左列、乗数 525 を右列に、上から整数部分・分子・分母の順に並べる。

(2)

それぞれの数で整数部分と分母の積を取り、分子に加える。被乗数は 3 × 3 + 1 = 10 、乗数は 5 × 5 + 2 = 27 となる。

(3)

分子どうし積を取り、10 × 27 = 270 を新たな分子とする。

(4)

分母どうし積を取り、3 × 5 = 15 を新たな分母とする。

(5)

先述の手順に従って、分子270を分母15で割ると図のようになる。最終的に現れた 18015 = 18 が求める解である。

最大公約数と約分

『九章算術』では約分術という名で分母と分子の最大公約数を求めて約分を行うアルゴリズムが記載されている。分母と分子のうち大きい方から小さい方を引き、それを繰り返していって分母と分子が等しくなるとそれが最大公約数である^[3]^:20。この方法はユークリッドの互除法と同一のものである^[3]^:20。600/375 の最大公約数75を求める手順を以下に示す。

(1)

(2)

(3)

(4)

(5)

分母分子をそれぞれ最大公約数75で割れば、約分された 8/5 が得られる。

内挿法

暦学者で数学者の何承天は、分数による一種の内挿法である「調日法（中国語版）」を考案した。まず未知の実数をそれより大きい分数（強率）と小さい分数（弱率）で挟む。強率および弱率の分母どうし・分子どうしをそれぞれ足して新しい分数を作り、強率もしくは弱率と置き換える。この計算を繰り返すことで、未知数の近似値を求める方法である^[11]。祖沖之が得た名高い近似値 $π$ = 355/113 は調日法で求めることができる^[12]。

連立一次方程式

『九章算術』巻第八「方程」にはガウスの消去法に似た連立一次方程式の解法が述べられている^[13]。以下を例題とする。

〔一〕今有上禾三秉，中禾二秉，下禾一秉，實三十九斗；上禾二秉，中禾三秉，下禾一秉，實三十四斗；上禾一秉，中禾二秉，下禾三秉，實二十六斗。問上、中、下禾實一秉各幾何？ (中国語) 九章算術, ウィキソースより閲覧。

（訳）上等の稲が3束、中等の稲が2束、下等の稲が1束あり、これらの実を合わせると39斗になる。それぞれ2束、3束、1束であれば34斗となり、1束、2束、3束であれば26斗となる。それぞれの稲1束当たりの実は何斗か？

代数的にはこの問題は三元連立方程式で表される。

{\begin{aligned}3x+2y+z&=39\\2x+3y+z&=34\\x+2y+3z&=26\\\end{aligned}}

『九章算術』では、算盤上に4×3行列のような形式で並べた棒を数えることでこの問題を解いている^[3]^:143-151。

	左列	中列	右列
上等
中等
下等
実

アルゴリズムは以下の通りである。

右列の一番上の値を中列にかける。

	左列	中列	右列
上等
中等
下等
実

中列の一番上の値が0になるまで、中列から右列を繰り返し引く。

	左列	中列	右列
上等
中等
下等
実

同様の手順により、右列を用いて左列を縮約する。

	左列	中列	右列
上等
中等
下等
実

縮約された中列を用いて、左列をさらに縮約する。その結果三角行列のような配置が得られる。

	左列	中列	右列
上等
中等
下等
実

左列に作られた数から、下等の稲1束当たりの実は 99/36 = 23/4 斗と求められる。

この結果を用いれば、上等および中等の稲についてそれぞれ 91/4 斗、 41/4 斗の値を得るのは容易である。

開平法

籌算による開平計算のアルゴリズムは開方術として『九章算術』に記載されており、いくらか用語は異なるが『孫子算経』にも記述がある。

『孫子算経』中巻第19問に平方根の近似値 ${\sqrt {234567}}\approx 484{\tfrac {311}{968}}$ を求める問題がある^[14]。

今有積二十三萬四千五百六十七步。問：為方幾何？答曰：四百八十四步九百六十八分步之三百一十一。 (中国語) 孫子算經, ウィキソースより閲覧。

この計算アルゴリズムを以下に示す。

(1)

算盤の2段目（実（實））に数234567を作る。4段目（下法）の10000の位に1を置く。

						商
						実
						方法
						下法

(2)

平方根の1桁までを400と見積もり、1段目（商）の100の位に4を置く。商と下方の積 1 × 4 = 4 を取り、3段目（方法）に書く。

						商
						実
						方法
						下法

(3)

実の「23」から商と方法の積 4 × 4 = 16 を差し引き、 23 − 16 = 7 を残す。

						商
						実
						方法
						下法

(4)

方法の4を2倍にして、1桁ぶん右に動かす（縦式を横式に変える）。次に下法を2桁ぶん右に動かす。

						商
						実
						方法
						下法

(5)

平方根の2桁目を8と見積もり、商の10の位に8を置く。次に、今加わった桁の「8」と下方1との積を取り、方法に加える。

						商
						実
						方法
						下法

(6)

方法第1桁の「8」に第2桁の「8」をかけ、その積を実の「74」から差し引く。その結果 74 − 8 × 8 = 10 が実に残る。

						商
						実
						方法
						下法

(7)

次に、方法第2桁の「8」を自乗したものを、実の「105」から差し引く。その結果 105 − 8 × 8 = 41 が実に残る。

						商
						実
						方法
						下法

(8)

方法88の最終桁「8」を2倍して、最終桁を除いた「80」に加える。方法は 80 + 8 × 2 = 96 となる。

						商
						実
						方法
						下法

(9)

方法を右に1桁ぶん移す。次に、下法を右に2桁ぶん移す。

						商
						実
						方法
						下法

(10)

平方根の3桁目を4と見積もり、商に記す。次に、今加わった4と下方1との積を取り、方法に加えて964とする。

						商
						実
						方法
						下法

(11)

方法の第1桁の9に第3桁の4をかけて、その積を実の「41」から差し引く。その結果 41 − 9 × 4 = 5 が実に残る。

						商
						実
						方法
						下法

(12)

続いて、方法の第2桁の6に第3桁の4をかけて、その積を実の「56」から差し引く。その結果 56 − 6 × 4 = 32 が実に残る。

						商
						実
						方法
						下法

(13)

さらに、方法の第3桁の4を自乗したものを実の「27」から差し引く。その結果 27 − 4 × 4 = 11 が実に残る。

						商
						実
						方法
						下法

(14)

方法の第3桁の4を2倍して、第3桁を除いた960に加え、968とする。

						商
						実
						方法
						下法

最後に残った商の484、実の311、方法の968は、求める平方根 ${\sqrt {234567}}\approx 484{\tfrac {311}{968}}$ を表している。

北宋の数学者賈憲（中国語版）は、開平計算の途中で「方法」を2倍する代わりに、効果は変わらないが「商」の1桁を「方法」に加えるアルゴリズムを発展させた。

開立法

『九章算術』巻第四「少広」には立方根を求める方法（開立方術）が記載されている。

〔一九〕今有積一百八十六萬八百六十七尺。問為立方幾何？答曰：一百二十三尺。 (中国語) 九章算術, ウィキソースより閲覧。

（訳）問19：体積が1860867立方尺の立方体がある。1辺の長さはいくらか？解：123尺。

現代の表記法では、この問題は以下のように書かれる。

{\sqrt[{3}]{1860867}}=123

賈憲はホーナー法を単純化した開立法を発明した。右のアニメーションは賈憲のアルゴリズムで上の問題を解く手順を示したものである。

代数方程式

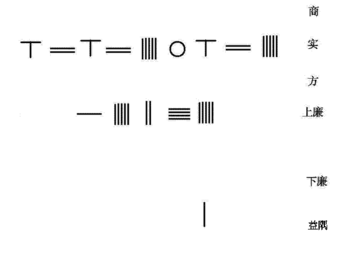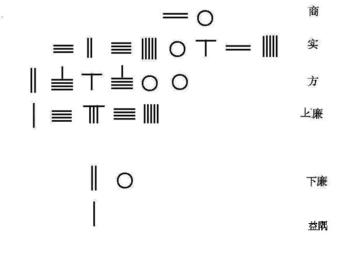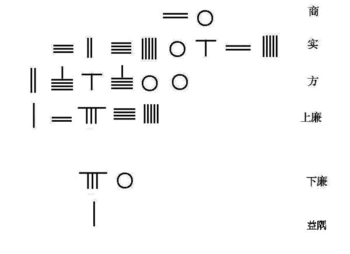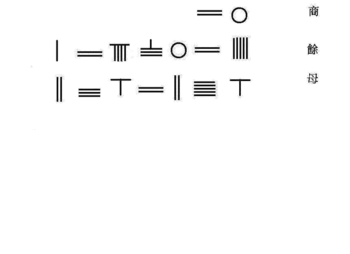
賈憲は以下の形式を持つ単純な4次方程式をホーナー法によって解く方法を考案した。

x^{4}=a

南宋の数学者秦九韶は賈憲のホーナー法を発展させ、10次までの代数方程式を解いた。秦の著書『数書九章』第六巻問二で提示された方程式^[15]

-x^{4}+15245x^{2}-6262506.25=0

から解

x=20{\frac {1298025}{2362256}}

を求めるアルゴリズムを右のアニメーションに示す。この方程式は、算盤上に以下の表のように置かれた算木の配置から構成したものである。


0	商	（根）
626250625	實（実）	（定数）
0	方	（ $x$ の係数）
15245	上廉	（ $x 2$ の正係数）
0	負廉	（ $x 2$ の負係数）
0	下廉	（ $x 3$ の係数）
1	益隅	（ $x 4$ の負係数）

天元術

→詳細は「天元術」を参照

高次方程式の解法である天元術は12世紀ごろに生まれたと考えられている。このころ未知数の記号は用いられていなかったため、次数の順に並べた各項の係数を算木数字の列とすることで方程式を表現していた^[6]^:159。元代の数学者李冶は天元術の表記を洗練させた^[7]。

李冶の『測円海鏡（zh）』第二巻、第十四問で提示されている一元方程式

-x^{2}-680x+96000=0

は天元術では以下のように表される。それぞれの段の数字が未知数各次の係数を表す。1次の段には「元」の字を記す^[7]。


					元

四元術

元の数学者朱世傑は天元術をさらに発展させ、二元から四元までの代数方程式を扱う方法を考案した^[7]。朱が著した『四元玉鑑（中国語版）』では四元はそれぞれ天、地、人、物と呼ばれていた。四元を未知数 $x$ 、 $y$ 、 $z$ 、 $u$ で表し、いくつかの数式を例として算木式で表記する^[1]^:90。

例 (1): $x-2y+3z-4w+4$


	太

例 (2): $x^{2}+4y^{2}+9z^{2}-16w^{2}-4xy+6xz+16yw-24zw-2yz$


	太

脚注

^ ^a ^b ^c ^d ^e ^f 薮内清『中国の数学』岩波書店〈岩波新書青版59〉、1974年。ISBN 4004160596。
^ ^a ^b 三浦國雄「算木」『世界大百科事典』 11巻（改定新版）、平凡社、2005年。
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j 孫栄健『古代中国数学「九章算術」を楽しむ本』言視社、2016年。ISBN 486565044X。
^ ^a ^b ^c ^d ^e ジョゼフ・ニーダム『中国の科学と文明第4巻』（新版）思索社、1991年。ISBN 4-7835-0193-9。
^ 鈴木景二「算木と古代実務官」『木簡研究』第18巻、1996年、247-264頁。
^ ^a ^b ^c 李迪著、大竹茂雄、陸人瑞訳『中国の数学通史』森北出版、2002年。ISBN 4-627-01941-6。
^ ^a ^b ^c ^d ^e 薮内清「中国数学」『世界大百科事典』 18巻（改定新版）、平凡社、2005年。
^ Colin A. Ronan (1985). “1”. The Shorter Science and Civilisation in China. 2. Cambridge University Press. ISBN 9780521315364
^ Ho Peng Yoke (2000). Li, Qi and Shu: An Introduction to Science and Civilization in China. Dover Science Books. Dover Publications. ISBN 0486414450
^ Lam 1992, pp. 87-88
^ Martzloff 2006, p. 281
^ Wu Wenjun, ed. Grand Series of History of Chinese Mathematics. 4. p. 125
^ Martzloff 2006, pp. 249-257
^ Lam 1992, pp. 66-73
^ Martzloff 2006, pp. 233-246

参考文献

Lam Lay Yong（藍麗蓉）; Ang Tian Se（洪天賜） (1992). Fleeting Footsteps. World Scientific. ISBN 981-02-3696-4
Jean-Claude Martzloff (2006). A History of Chinese Mathematics. Springer. ISBN 978-3-540-33782-9

器具