読み上げ数列
表示
この項目「読み上げ数列」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:en:Look-and-say sequence 11:06, 7 August 2021) 修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。ノートページや履歴も参照してください。(2021年9月) |
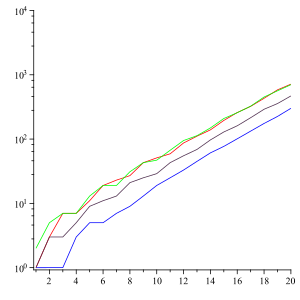
読み上げ数列(よみあげすうれつ、英:look-and-say sequence)とは、数学において次のように始まる整数列である。
1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... (オンライン整数列大辞典の数列 A005150)
前の数列から次の数列を生成するには、前の数列の桁を読み取り、同じ桁のグループの桁数を数える。
例えば...
- 1は「1個の1」のため、11と表記する。
- 11は「2個の1」のため、21と表記する。
- 21は「1個の2と1個の1」のため、1211と表記する。
- 1211は「1個の1、1個の2、2個の1」のため、111221と表記する。
- 111221は「3個の1、2個の2、1個の1」のため、312211と表記する。
︙
このような規則性に則って、数列が増えていく。
読み上げ数列は、ジョン・ホートン・コンウェイによって導入および分析された[1]。
読み上げ数列の考え方は、ランレングスエンコーディングの考え方と似ている。
0から9までの任意の数字dで開始した場合、dは数列の最後の数字として無期限に残る。 1以外のdの場合、数列は次のようになる。
- d 、1 d 、111 d 、311 d 、13211 d 、111312211 d 、31131122211 d 、…
d = 3から始まるこの数列をコンウェイ数列と呼んでいる。 ( d = 2については、 OEIS参照: オンライン整数列大辞典の数列 A005150 ) [2]
基本的な特性・性質
[編集]
成り立ち
[編集]数列は無期限に大きくなる。実際には、異なる整数シード番号から始まることによって定義された任意の変異体は、最終的には無限に成長する[3]。
数字の存在制限
[編集]1、2、および3以外の数字は、シード番号にそのような数字または同じ数字の3つを超えるランが含まれていない限り、シーケンスに表示されない[3]。
出典
[編集]- ^ Conway, John (January 1986). “The Weird and Wonderful Chemistry of Audioactive Decay”. Eureka 46: 5–16.
- ^ Conway Sequence, MathWorld, accessed on line February 4, 2011.
- ^ a b Martin, Oscar (2006). “Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA”. American Mathematical Monthly (Mathematical association of America) 113 (4): 289–307. doi:10.2307/27641915. ISSN 0002-9890 January 6, 2010閲覧。.
