逐次一貫性
逐次一貫性(ちくじいっかんせい、英語: sequential consistency)、順次整合性(じゅんじせいごうせい)、逐次整合性(ちくじせいごうせい)は並行プログラミングにおける一貫性モデルの一種である。「どのような実行結果も、すべてのプロセッサがある順序で逐次的に実行した結果と等しく、かつ、個々のプロセッサの処理順序がプログラムで指定された通りであること」と定義されている[1]。
この記述を理解するためには、同一プロセッサ(またはスレッド)内でのプログラムの実行順序はプログラムの順序と同じであるが、プロセッサ(またはスレッド)間でのプログラムの実行順序は未定義であることを理解する必要がある。以下の例では
プロセッサー 1: <-- A1 run --> <-- B1 run --> <-- C1 run --> プロセッサー 2: <-- A2 run --> <-- B2 run --> 時間 --------------------------------------------------------------------->
A1、B1、C1の実行順序は維持される。つまりA1はB1の前、B1はC1の前に実行される。A2とB2についても同様である。しかしプロセッサ間の実行順序は未定義であるため、B2がC1の前または後に実行される可能性がある(物理的にはB2がC1の前に実行されるかもしれないが、B2の効果がC1の効果の後に現れるかもしれない。)
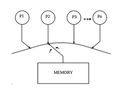
概念的には、単一のグローバルメモリと、任意のプロセッサを任意の時間ステップでメモリに接続する「スイッチ」が存在する。各プロセッサはプログラム順にメモリ操作を行い、スイッチはすべてのメモリ操作間のグローバルな直列化を行う。
同じメモリー部分(ページ、仮想オブジェクト、セル等)に対する書き込み操作がすべてのノードにおいて同じ順序で観測されるならば、たとえその順序が実際に操作が行われた時間順序とは異なっていたとしても、そのシステムでは逐次一貫性が保証される。
逐次一貫性は厳密な一貫性(英語: strict consistency)(これはすべての操作が発行された順序で実行されることを求める。ただし、分散並列システムでは大域的な時間を決定することができないので、実現不能である。)よりも緩やかな一貫性モデルである。
関連項目
[編集]脚注
[編集]- ^ Leslie Lamport, "How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs", IEEE Trans. Comput. C-28,9 (Sept. 1979), 690-691.