出典: フリー百科事典『ウィキペディア(Wikipedia)』
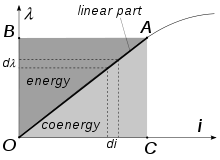 随伴エネルギー (coenergy) の定義を図で表したもの。
随伴エネルギー (coenergy) の定義を図で表したもの。
物理学や工学において、随伴エネルギー (英: coenergy, co-energy) とはエネルギーの単位で測られる仮想的な量であり、物理系のエネルギーを理論的に分析するときに使われる。[1]
随伴エネルギーの概念は多くの保存系(慣性系における力学系、電磁場系等)に適用できる。このとき、これらの系にはエネルギーの入力量と蓄積量の間に線形の関係があることが求められる。
随伴エネルギーによる解析は非線形の系には適用できない。しかしながら、非線形性が小さいときには線形化によって見逃される。
単一のコイルと固定された接極子からなる系では力学的仕事はない。そのため、この系に供給された電気エネルギーはすべて磁場に蓄積される[1]。

ここで、e を電圧、i を電流、λ を鎖交磁束として


と表せ、そのため

が成り立つ。一般の問題では、i と λ の関係は非線形になる(磁気ヒステリシス(英語版)を参照)。
鎖交磁束に有限の変化があった時(たとえば λ1 から λ2 へ)、蓄積されるエネルギーは次のように求められる。

(変化が周回であった場合には、ヒステリシスおよび渦電流のためにエネルギー損失が生じる。これらの損失は入力エネルギーから賄われ、したがってコイルに対する鎖交磁束は影響を受けず、コイルは損失のない理想的なものとして扱うことができる。このようなシステムが保存系とみなせる。)
計算において、鎖交磁束 λ または 電流 i のどちらかが独立変数となる。
システムに蓄えられたエネルギー総量は図のOABOの面積に等しく、これはまたOACOに等しい、したがって以下のように表せる。


線形の無損失な系において、随伴エネルギーは蓄積されているエネルギーに等しい。随伴エネルギーは現実の物理意味は持たないが、電磁的な系の力学的計算においては有用である。式の上では、実際のエネルギーと区別するために、随伴エネルギーにはプライム記号をつけておくことが多い。
矩形OCABOの全面積はふたつの三角形の面積の和(エネルギー+随伴エネルギー)に等しい。

そのため、電流 i、鎖交磁束 λ の点に対して

自己インダクタンスは鎖交磁束を電流で割ったものと定義される。

すると、コイルに蓄えられたエネルギーは以下となる。

ここで注意するべきこととして、可動な接極子をもつ磁気回路中ではインダクタンス L (x) は位置 x の関数である。したがって場のエネルギーは数学的に独立な2変数 λ および x の関数となる。

随伴エネルギーについても独立変数 i および x の関数である。

最後の二つの式は磁気的な系のエネルギーと随伴エネルギーに対する一般的な表式である。
随伴エネルギーの概念は有限要素解析において、磁化した部分の間での力学的な力を計算するうえでよく用いられる。
- ^ a b U.A. Bakshi, M.V. Bakshi, Electrical Machines - I, Technical Publications Pune, India, May 2006, ISBN 81-8431-225-3, page 11














