ポリオミノ

ポリオミノ(英: polyomino)は、複数の同じ大きさの正方形を辺どうしでつなげた多角形。正方形1つの場合も含む。また、それを長方形など指定の形に隙間なく並べるパズル。ソロモン・ゴロムが1953年に考案した[1]。
個の正方形をつなげた図形は -オミノといい、 には数字や、ギリシア語(またときにラテン語)を由来としたその数を意味する倍数接頭辞が入る[2]。
名称の由来
[編集]ポリオミノの名称は「多くの」をあらわす接頭語の poly- と、omino からきている。
omino とは、同じ大きさの2つの正方形が辺どうしでつながった形のドミノ domino を d- と omino に分解して作った造語であり、ドミノを構成する正方形を意味する。
ポリオミノを好む人たちを英語では ominist と呼ぶ。芦ケ原伸之はこれを「ミノ虫」と訳した[3]。
ポリオミノの種類と数
[編集]
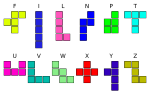

| 名称 | 両面[4] | 片面[5] | 有向[6] | |
|---|---|---|---|---|
| 1 | モノミノ | 1 | 1 | 1 |
| 2 | ドミノ | 1 | 1 | 2 |
| 3 | トロミノ/トリオミノ | 2 | 2 | 6 |
| 4 | テトロミノ | 5 | 7 | 19 |
| 5 | ペントミノ | 12 | 18 | 63 |
| 6 | ヘキソミノ | 35 | 60 | 216 |
| 7 | ヘプトミノ | 108 | 196 | 760 |
| 8 | オクトミノ | 369 | 704 | 2,725 |
| 9 | ノノミノ | 1,285 | 2,500 | 9,910 |
| 10 | デコミノ | 4,655 | 9,189 | 36,446 |
| 11 | ウンデコミノ | 17,073 | 33,896 | 135,268 |
| 12 | ドデコミノ | 63,600 | 126,759 | 505,861 |
| 13 | トリデコミノ | 238,591 | 476,270 | 1,903,890 |
| 14 | クアドルデコミノ | 901,971 | 1,802,312 | 7,204,874 |
| 15 | クインデコミノ | 3,426,576 | 6,849,777 | 27,394,666 |
- 「両面」とは、回転するか裏返しすれば重なる場合は同じ図形と考えるもの。
- 「片面」とは、回転すれば重なる場合は同じ図形と考え、裏返さなければ重ならない場合は別の図形と考えるもの。
- 「有向」とは、向きが異なるものは全て異なると考えるもの。平行移動で重なる場合は同じ図形と考える。
箱詰めパズル
[編集]
ポリオミノを長方形などの箱に敷き詰めるパズルが多数考案されている。 特にペントミノを6x10などの長方形に敷き詰めるパズルが有名である。 また、敷き詰める以外の条件を設定したパズルも多い。
ドミノの角が十字に集まらないように敷き詰めるパズルは、畳の敷き方として親しまれてきた。
これ以外にも例えば以下のような条件が与えられることがある。
- 単位正方形を長方形や平行四辺形などに変形し、回転に制限を与える。
- 図形を単位正方形で市松模様に色分けし、全体で市松模様になるように敷き詰める。
- 箱の形を固定せず、合同形を複数作る、対称形にするなど条件を満たす形に並べる。
- 同形のポリオミノで長方形を作る[7](p151)。
正方形以外への応用
[編集]ポリオミノの正方形の代わりに、いくつかの別の図形を使った多角形には、名前がついている。これらを総称してポリフォームと呼ぶことがある。
ポリオミノと同様に、これらの図形を用いた箱詰めパズルも考案されている。 これらの一部は、テンヨーから「プラパズル」の商品名で市販されている。
ポリオミノを使ったゲーム
[編集]
- ドミノ
- ポリオミノの名前の由来となったボードゲーム。
- 0~6、もしくは0~9のサイコロの目が各正方形に描かれた一式の牌を用いる。
- テトリス
- 「片面型テトロミノ」7種を用いた落ち物パズル。
- このゲームでは『テトリミノ』の名称が使用される。
- ブロックス
- 両面型モノミノ~ペントミノの計21個の牌を盤に置くボードゲーム。
ハナヤマから「明治パズルシリーズ」として、チョコレートなどのお菓子をモチーフにしたポリオミノが(2022年現在)発売されている[8][9]。
脚注
[編集]- ^ Brian Kell. “21-110: Polyominoes Introduction” (英語). 2023年11月10日閲覧。
- ^ Greek Numerical Prefixes
- ^ 芦ヶ原伸之『パズラート パズルの回帰線』P.72
- ^ オンライン整数列大辞典の数列 A000105
- ^ オンライン整数列大辞典の数列 A000988
- ^ オンライン整数列大辞典の数列 A001168
- ^ 土橋創作; 池野信一、高木茂男、中村義作 (1976). 数理パズル. 中公新書
- ^ http://www.hanayamatoys.co.jp/product/category/puzzle/meiji.html
- ^ “明治チョコレートパズル”. 2023年11月10日閲覧。


