テイト方程式 (テイトほうていしき、英 : Tait equation )は、流体力学 において、液体密度 と静水圧圧力 を関連付ける状態方程式 である。この方程式は1888年にピーター・ガスリー・テイト によって発表され、以下の形で表される[ 1]
V
0
−
V
P
V
0
=
A
Π
+
P
{\displaystyle {\frac {V_{0}-V}{PV_{0}}}={\frac {A}{\Pi +P}}}
ここで、
P
{\displaystyle P}
V
0
{\displaystyle V_{0}}
V
{\displaystyle V}
P
{\displaystyle P}
A
{\displaystyle A}
Π
{\displaystyle \Pi }
A
{\displaystyle A}
Π
{\displaystyle \Pi }
[ 2]
1895年には[ 3] [ 4]
K
=
−
V
0
(
∂
P
∂
V
)
T
=
V
0
(
B
+
P
)
C
{\displaystyle {K}=-{V_{0}}\left({\frac {\partial P}{\partial V}}\right)_{T}={V_{0}}{\frac {(B+P)}{C}}}
ここで、
K
{\displaystyle K}
V
=
V
0
−
C
log
(
B
+
P
B
+
P
0
)
{\displaystyle V=V_{0}-C\log \left({\frac {B+P}{B+P_{0}}}\right)}
ここで、
V
{\displaystyle V}
比容積 (単位はml /g またはm3 /kg)、
V
0
{\displaystyle V_{0}}
P
=
P
0
{\displaystyle P=P_{0}}
B
{\displaystyle B}
P
0
{\displaystyle P_{0}}
C
{\displaystyle C}
V
0
{\displaystyle V_{0}}
温度 の関数である。
比容積から見た圧力の式は次のようになる。
P
=
(
B
+
P
0
)
exp
(
−
V
−
V
0
C
)
−
B
{\displaystyle P=(B+P_{0})\exp \left(-{\frac {V-V_{0}}{C}}\right)-B\,}
テイト・タンマン状態方程式に関する研究では、経験的パラメータ
C
{\displaystyle C}
B
{\displaystyle B}
[ 2]
T
c
{\displaystyle T_{c}}
C
{\displaystyle C}
B
{\displaystyle B}
[ 5] 三重点 温度から148Kまでの範囲で詳細に扱われており、これは参考文献の第6節に記載されている[ 6]
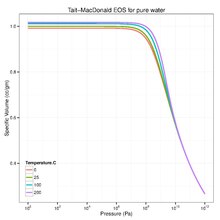
テイト・マーナハン状態方程式により予測される、圧力の関数としての比容積。 もう一つのテイト方程式として広く知られる[ 7] [ 8] [ 9]
V
V
0
=
[
1
+
n
K
0
(
P
−
P
0
)
]
−
1
/
n
{\displaystyle {\frac {V}{V_{0}}}=\left[1+{\frac {n}{K_{0}}}\,(P-P_{0})\right]^{-1/n}}
ここで、
V
{\displaystyle V}
P
{\displaystyle P}
V
0
{\displaystyle V_{0}}
P
0
{\displaystyle P_{0}}
K
0
{\displaystyle K_{0}}
P
0
{\displaystyle P_{0}}
n
{\displaystyle n}
この式は、圧力式で次のように置き換えられる。
P
=
K
0
n
[
(
V
0
V
)
n
−
1
]
+
P
0
=
K
0
n
[
(
ρ
ρ
0
)
n
−
1
]
+
P
0
{\displaystyle P={\frac {K_{0}}{n}}\left[\left({\frac {V_{0}}{V}}\right)^{n}-1\right]+P_{0}={\frac {K_{0}}{n}}\left[\left({\frac {\rho }{\rho _{0}}}\right)^{n}-1\right]+P_{0}}
ここで、
ρ
,
ρ
0
{\displaystyle \rho ,\rho _{0}}
P
,
P
0
{\displaystyle P,P_{0}}
[要出典 。
P
0
{\displaystyle P_{0}}
ρ
0
{\displaystyle \rho _{0}}
K
0
{\displaystyle K_{0}}
n
{\displaystyle n}
この形のテイト状態方程式は、マーナハンの状態方程式 の形と同一であることに注意する必要がある。
マクドナルド・テイトモデルによって予測される接線体積弾性率は以下の通りである。
K
=
K
0
(
V
0
V
)
n
{\displaystyle K=K_{0}\left({\frac {V_{0}}{V}}\right)^{n}\,}
純水の実験データへのフィットに基づくトゥムリルツ・テイト・タンマン状態方程式。 液体のモデル化に使用できる関連する状態方程式として、トゥムリルツ方程式(時にタンマン方程式とも呼ばれる。)がある。この方程式は、最初にトゥムリルツが1909年に提案し、タンマンが1911年に純水のために再提案した[ 4] [ 10]
V
(
P
,
S
,
T
)
=
V
∞
−
K
1
S
+
λ
P
0
+
K
2
S
+
P
{\displaystyle V(P,S,T)=V_{\infty }-K_{1}S+{\frac {\lambda }{P_{0}+K_{2}S+P}}}
V
(
P
,
S
,
T
)
{\displaystyle V(P,S,T)}
P
{\displaystyle P}
S
{\displaystyle S}
T
{\displaystyle T}
V
∞
{\displaystyle V_{\infty }}
P
=
∞
{\displaystyle P=\infty }
K
1
{\displaystyle K_{1}}
K
2
{\displaystyle K_{2}}
P
0
{\displaystyle P_{0}}
淡水(
S
=
0
{\displaystyle S=0}
V
=
V
∞
+
λ
P
0
+
P
{\displaystyle V=V_{\infty }+{\frac {\lambda }{P_{0}+P}}\,}
純水の場合、
V
∞
{\displaystyle V_{\infty }}
λ
{\displaystyle \lambda }
P
0
{\displaystyle P_{0}}
[ 10]
λ
=
1788.316
+
21.55053
T
−
0.4695911
T
2
+
3.096363
×
10
−
3
T
3
−
0.7341182
×
10
−
5
T
4
P
0
=
5918.499
+
58.05267
T
−
1.1253317
T
2
+
6.6123869
×
10
−
3
T
3
−
1.4661625
×
10
−
5
T
4
V
∞
=
0.6980547
−
0.7435626
×
10
−
3
T
+
0.3704258
×
10
−
4
T
2
−
0.6315724
×
10
−
6
T
3
+
0.9829576
×
10
−
8
T
4
−
0.1197269
×
10
−
9
T
5
+
0.1005461
×
10
−
11
T
6
−
0.5437898
×
10
−
14
T
7
+
0.169946
×
10
−
16
T
8
−
0.2295063
×
10
−
19
T
9
{\displaystyle {\begin{aligned}\lambda &=1788.316+21.55053\,T-0.4695911\,T^{2}+3.096363\times 10^{-3}\,T^{3}-0.7341182\times 10^{-5}\,T^{4}\\P_{0}&=5918.499+58.05267\,T-1.1253317\,T^{2}+6.6123869\times 10^{-3}\,T^{3}-1.4661625\times 10^{-5}\,T^{4}\\V_{\infty }&=0.6980547-0.7435626\times 10^{-3}\,T+0.3704258\times 10^{-4}\,T^{2}-0.6315724\times 10^{-6}\,T^{3}\\&+0.9829576\times 10^{-8}\,T^{4}-0.1197269\times 10^{-9}\,T^{5}+0.1005461\times 10^{-11}\,T^{6}\\&-0.5437898\times 10^{-14}\,T^{7}+0.169946\times 10^{-16}\,T^{8}-0.2295063\times 10^{-19}\,T^{9}\end{aligned}}}
温度
T
{\displaystyle T}
P
0
{\displaystyle P_{0}}
V
∞
{\displaystyle V_{\infty }}
λ
{\displaystyle \lambda }
圧力の比容積に対する逆トゥムリルツ・テイト・タンマン関係は次のようになる。
P
=
λ
V
−
V
∞
−
P
0
{\displaystyle P={\frac {\lambda }{V-V_{\infty }}}-P_{0}\,}
純水の即時接線体積弾性率 のトゥムリルツ・テイト・タンマン公式は、圧力
P
{\displaystyle P}
[ 4]
K
=
−
V
∂
P
∂
V
=
V
λ
(
V
−
V
∞
)
2
=
(
P
0
+
P
)
+
V
∞
λ
(
P
0
+
P
)
2
{\displaystyle K=-V\,{\frac {\partial P}{\partial V}}={\frac {V\,\lambda }{(V-V_{\infty })^{2}}}=(P_{0}+P)+{\frac {V_{\infty }}{\lambda }}(P_{0}+P)^{2}\,}
水中爆発の研究、特に発生する衝撃波に関連して、ジョン・G・カークウッド は1965年に[ 11]
−
1
V
(
∂
V
∂
P
)
S
=
1
n
(
B
+
P
)
{\displaystyle -{\frac {1}{V}}\left({\frac {\partial V}{\partial P}}\right)_{S}={\frac {1}{n(B+P)}}}
ここで、
S
{\displaystyle S}
n
{\displaystyle n}
B
{\displaystyle B}
n
{\displaystyle n}
B
{\displaystyle B}
P
{\displaystyle P}
積分を行うことで、等エントロピー条件(
S
{\displaystyle S}
V
(
P
,
S
)
{\displaystyle V(P,S)}
V
V
0
=
(
1
+
P
0
B
)
1
/
n
(
1
+
P
B
)
−
1
/
n
{\displaystyle {\frac {V}{V_{0}}}=\left(1+{\frac {P_{0}}{B}}\right)^{1/n}\left(1+{\frac {P}{B}}\right)^{-1/n}}
このとき、
V
0
=
V
(
P
0
,
S
)
{\displaystyle V_{0}=V(P_{0},S)}
である。
等エントロピー条件(
S
{\displaystyle S}
P
(
V
,
S
)
{\displaystyle P(V,S)}
P
=
(
B
+
P
0
)
(
V
0
V
)
n
−
B
{\displaystyle P=(B+P_{0})\,\left({\cfrac {V_{0}}{V}}\right)^{n}-B\,}
修正されたテイト状態方程式に関する詳細な研究では、2つの経験的パラメータ
n
{\displaystyle n}
B
{\displaystyle B}
[ 2]
また、水、ヘリウム3、ヘリウム4に対して、これらの経験的パラメータ
n
{\displaystyle n}
B
{\displaystyle B}
^ Tait, P. G. (1888). “Report on some of the physical properties of fresh water and of sea water”. Physics and Chemistry of the Voyage of H.M.S. Challenger . II, part IV ^ a b c Aitken, Frederic; Foulc, Jean-Numa (2019). From Deep Sea to Laboratory 3:From Tait's Work on the Compressibility of Seawater to Equations-of-State for Liquids ISBN 9781786303769 . http://www.iste.co.uk/book.php?id=1534
^ Tammann, G. (1895). “Über die Abhängigkeit der volumina von Lösungen vom druck”. Zeitschrift für Physikalische Chemie 17 : 620–636. ^ a b c Hayward, A. T. J. (1967). Compressibility equations for liquids: a comparative study. British Journal of Applied Physics, 18(7), 965. http://mitran-lab.amath.unc.edu:8081/subversion/Lithotripsy/MultiphysicsFocusing/biblio/TaitEquationOfState/Hayward_CompressEqnsLiquidsComparative1967.pdf
^ Aitken, F.; Volino, F. (November 2021). “A new single equation of state to describe the dynamic viscosity and self-diffusion coefficient for all fluid phases of water from 200 to 1800 K based on a new original microscopic model”. Physics of Fluids 33 (11): 117112. arXiv :2108.10666 . Bibcode : 2021PhFl...33k7112A . doi :10.1063/5.0069488 . ^ Aitken, Frédéric; Denat, André; Volino, Ferdinand (24 April 2024). “A New Non-Extensive Equation of State for the Fluid Phases of Argon, Including the Metastable States, from the Melting Line to 2300 K and 50 GPa”. Fluids 9 (5): 102. arXiv :1504.00633 . doi :10.3390/fluids9050102 . ^ Thompson, P. A., & Beavers, G. S. (1972). Compressible-fluid dynamics. Journal of Applied Mechanics, 39, 366.
^ Kedrinskiy, V. K. (2006). Hydrodynamics of Explosion: experiments and models. Springer Science & Business Media.
^ Macdonald, J. R. (1966). Some simple isothermal equations of state. Reviews of Modern Physics, 38(4), 669.
^ a b Fisher, F. H., and O. E. Dial Jr. Equation of state of pure water and sea water. No. MPL-U-99/67. SCRIPPS INSTITUTION OF OCEANOGRAPHY LA JOLLA CA MARINE PHYSICAL LAB, 1975. http://www.dtic.mil/dtic/tr/fulltext/u2/a017775.pdf
^ Cole, R. H. (1965). Underwater Explosions . New York: Dover Publications

















![{\displaystyle {\frac {V}{V_{0}}}=\left[1+{\frac {n}{K_{0}}}\,(P-P_{0})\right]^{-1/n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a792ef1b0a3bb29f077c3cdeffbcc0ce4a2043)


![{\displaystyle P={\frac {K_{0}}{n}}\left[\left({\frac {V_{0}}{V}}\right)^{n}-1\right]+P_{0}={\frac {K_{0}}{n}}\left[\left({\frac {\rho }{\rho _{0}}}\right)^{n}-1\right]+P_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/212dfd46c5dfa1585eb2b924a1b5a401252d3fb8)























