全方位720度矩形画像モニタリングシステム
全方位720度矩形画像モニタリングシステムは、球面状の全方位720度の世界地図情報をトポロジー的に正4面体に変換し、矩形に展開した平面画像が平面充填することによって、海洋も陸地も、隙間なく連続し、さらに時間を含む全方位720度の流体地理学的世界像を人間の視野が同時的に把握するモニタリングシステム[1]。時間を含む4次元の全方向性のモニタリングの概念は、3 wayのビューワー[1]で選択的に認識可能となった。
概要
[編集]


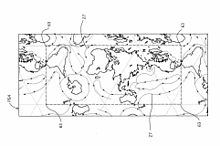
720度全方位矩形画像モニタリングシステムは、リモート分散型カメラなどによって撮影される画像から、互いに重複しない全方向かつ全視野に相当する720度srのシームレスな一つの球面画像として統合した後、球系多面体上に写像し、最終的に一定の縦横比をもった連続した矩形画像に変換し、矩形画像全体をほぼ同一の縦横比をもった矩形ビューアー内に取り込み、人間の視野角が一度に捉えるモニターに表示する。球状の情報を球状スクリーンに全方位全視野の画像を再現しても、人間の視野角ではその一部しか同時的に認識できない。




球状の情報を多面体に投影し平面に展開したダイマクション地図は、正二十面体を用いた全方位、2点間距離、面積比などをより正確に再現することに成功した最初の世界地図であるが、主に正三角形の再配列による展開図では「一つの海に浮かぶ一つの島」という表現目的のために大陸をいっさい分断させなかった結果、展開図の外形パターンは正三角形によるジグザグな輪郭線が現れる。よって複数のダイマクション地図で平面充填はできない。
720度全方位矩形画像モニタリングシステムは、全視野かつ全方向の画像処理および画像表示において不可避であったノイズを100%排除し、人間の視野角で一度で容易に認識できる矩形画像に変換する。
さらに、この矩形画像を時系列的な単位とし、2回回転対称操作によって該単位毎の各辺で該単位内の被写体と背景の少なくともどちらか一方がほぼシームレスに相互に連続するように平面充填して、被写体あるいは背景の時間的変化を検索する。時間と空間をシームレスに表示した連続性から、不連続的で局所的な変化のみが検出可能である。
球状世界での出来事、生命圏、対流圏、成層圏などにおける地理学、気象学、物理学的情報など、特に国際便航空路、気象観測図や人工衛星などの高速移動体に関する軌跡が分断されない。全方向カメラや複数の衛星を利用した全世界地図表示に最適な矩形の画像処理および画像表示方法によって、全方位の画像表示形式を現在の印刷形式やカメラのファインダー、モニターなどあらゆる認識上の標準となっている矩形形式に適合する。

正4面体の全方位的な世界地図法(テトラマ)
[編集]テトラマ(英:TETRAMA)は、シナジェティクス研究所同研究員の嶋あゆ子によって構造とパターンがデザインされ2005年6月8日に日本特許庁に特許出願された世界地図とその図法である[2]。図版の世界地図テトラマ制作では、バックミンスター・フラー(en:Buckminster Fuller)のダイマクション地図に使用された衛星地図情報を元に、各ドット毎に球面から正四面体へ変換するトポロジー的投影図法はシナジェティクスの研究者ロバート・グレー(Robert W. Gray)[3]が担当するとともに、投影された平面画像を元に梶川泰司によって概念がデザインされた。 商標登録第4969026号。2017年商標出願済。



全地球的な球状に形成された地理的情報地図に内接する正4面体に、トポロジー的に変換して投影された4つの全方位的画像を、同型な2個の連続した正6角形モジュールからなる正4面体の展開図に変換する世界地図の新たな投影図法である。
同型の2個の連続した正6角形状モジュールに変換された正4面体の展開図は、 隙間なく平面充填することも可能である[4]。
テトラマとこれまで一般的に利用されるメルカトル図法とを比較すると、陸地の形と面積比率の歪みが少ないことが特徴である。さらに、テトラマは、2個の連続した正6角形モジュールは、連続したまま正4面体に還元することも、正4面体から連続的にフラットに完全に折りたたむことできる。また、折りたたみ可能な複数個のテトラマによって、幾何学的な平面充填を可能とし、かつ、閉じた全地球の地理的情報を無限に連続させることが可能となった。全方位を捉えたバックミンスター・フラーのダイマクションマップの正20面体状展開図において、主に陸地を囲むようにして形成される正三角形状にジグザグに分断された海洋領域では平面での全方位性が不可能であったが、 テトラマは、平面での全方位性を実現させた世界初の正4面体地球儀モデルである。
テトラマは、球面情報をトポロジー的に変換して、2個の連続した正6角形モジュールからなる最小限の4面体にし、次に、連続した2個の同型モジュールを平面の展開図に変換することによって、数学的に存在する最大の視野角720度(=4面体の内角の総和)を人間の視覚範囲内で捉えることができる。
対向する2つの極から投影する投影図法(perspective projection)において、平面に投影した「方位図法」は、分離した2つの円形状の地図になるが、テトラマの技法によって、対向する2つの極は、2つの互いに連続した同型モジュールの各正6角形の中心に設定できるので、各半球状の地理情報は、連続した正確に同型の正6角形に変換される。さらに、折りたたみ可能な正4面体のサーフィスモデルは、4面体と平面とを連続したまま往復できる。
また、全地球的な地理情報地図以外の、宇宙的な天球儀情報地図または全方位的な球面画像を、正4面体にトポロジー的変換された全方位的なテトラマの平面画像は、つねに連続した2個の正6角形状モジュールの全外形線に対して、2回回転対称性を維持しながら隙間なく無限に平面充填することができる。
光学原理的に広角レンズでの画角は180度以上を越えられない。さらに最大の視野角として全景をとらえてきたパノラマ(PANORAMA)の概念は、数学的な操作方法からもたらされた円筒に投影された360度の視野角をけっして超えられなかった。これらの投影図法の歴史的批判から、正4面体が本質的に有する全方位をとらえる720度の視野角の概念が発見され、正4面体状の全方位地図および全方位画像を有するシナジェティクスモデルに対してテトラマ(TETRAMA)と命名された(『 宇宙エコロジー』バックミンスター・フラー、梶川泰司 著 流体地理学の誕生 自己エコロジーのための全方位カメラ(ジオスコープ) P338~P345 参照 2004年 美術出版社)。
教育
[編集]2009年、東京パナソニックセンター内の体験型ミュージアムリスーピアで開催された日本数学教育学会主催のキッズスクールにてテトラマ®教材として使用された。同時に世界地図テトラマ®・アニメーションも上映された。
