函数的平方根

数学において函数的平方根（かんすうてきへいほうこん、英: functional square root）あるいは半反復（half iterate）とは、合成の演算に関する函数の平方根のことである。言い換えると、ある函数 $g$ の函数的平方根 $f$ とは、すべての $x$ に対して $f (f (x)) = g (x)$ を満たすもののことを言う。

例えば、 $f (x) = 2 x 2$ は $g (x) = 8 x 4$ の函数的平方根である。

同様に、チェビシェフ多項式 $g (x) = T n (x)$ の函数的平方根は $f (x) = cos (\sqrt n arccos(x))$ である。これは一般には多項式ではない。

また、 $f (x) = x /(\sqrt 2 + x (1-\sqrt 2))$ は $g (x) = x /(2- x)$ の函数的平方根である。

$f$ が $g$ の函数的平方根であることは、 $f = g [½]$ あるいは $f = g ½$ と表記される。

指数函数の函数的平方根は、1950年にヘルムート・クネーザーによって研究された^[1]。

ℝ 上での $f (f (x)) = x$ の解（実数の対合）は、1815年にチャールズ・バベッジによって初めて研究された。この方程式はバベッジの函数方程式と呼ばれる^[2]。特殊解は $bc \neq -1$ に対して $f (x) = (b - x)/(1 + cx)$ である。これは $c = 0$ あるいは $| b | ≅ | c | ≫ 1$ ( $f (x) = 1/ x$ ) を含む。バベッジは、任意の与えられた解 $f$ に対して、任意の可逆函数 $Ψ$ による函数的共役 $\Psi ^{-1}\circ f\circ \Psi$ もまた解であることを注記している。

任意の函数的 $n$ -乗根（ $n = ½$ だけでなく、連続、負、無限小の $n$ も含む）をシステマティックに構成する手順は、シュレーダーの方程式の解に依る^[3]^[4] ^[5]。

例

正弦函数（青）の第一半周期における反復。半反復（橙）、すなわち正弦函数の函数的平方根；さらにそれの函数的平方根、すなわち4分の1乗根（黒）；第二反復から始まる、その四回反復（赤）；それらを包含する緑の三角形は、極限の 0 反復を表し、正弦函数を導く始点を提供するのこぎり歯函数。一般教育的なウェブサイト^[6]より引用。

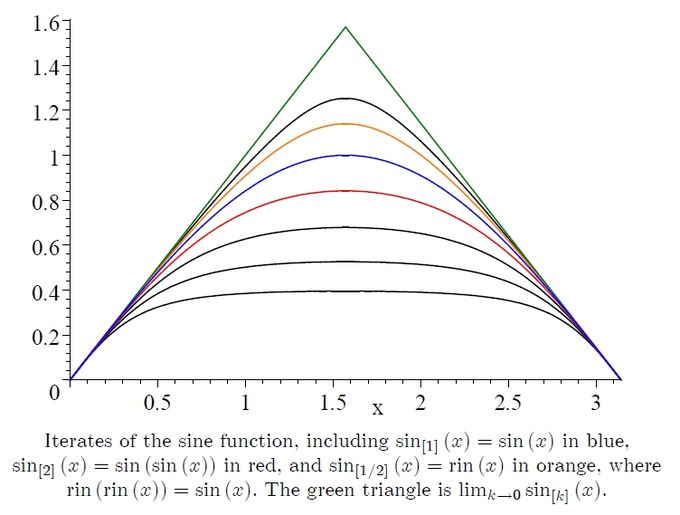
sin [2] (x) = sin(sin(x))

[赤の曲線]

sin [1] (x) = sin(x) = rin(rin(x))

[青の曲線]

sin [½] (x) = rin(x) = qin(qin(x))

[橙の曲線]

sin [¼] (x) = qin(x)

[橙の曲線より上にある黒の曲線]

sin [-1] (x) = arcsin(x)

[図示されていないが、緑の曲線より上にある。]

参考文献

^ Kneser, H. (1950). “Reelle analytische Lösungen der Gleichung φ(φ(x)) = e^x und verwandter Funktionalgleichungen”. Journal fur die reine und angewandte Mathematik 187: 56–67.
^ Jeremy Gray and Karen Parshall (2007) Episodes in the History of Modern Algebra (1800–1950), American Mathematical Society, ISBN 978-0-8218-4343-7
^ Schröder, E. (1870). “Ueber iterirte Functionen”. Mathematische Annalen 3 (2): 296–322. doi:10.1007/BF01443992.
^ Szekeres, G. (1958). “Regular iteration of real and complex functions”. Acta Mathematica 100 (3–4): 361–376. doi:10.1007/BF02559539.
^ Curtright, T.; Zachos, C. (2011). “Approximate solutions of functional equations”. Journal of Physics A 44 (40): 405205. doi:10.1088/1751-8113/44/40/405205.
^ Curtright, T.L. Evolution surfaces and Schröder functional methods.

この項目は、解析学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（プロジェクト:数学／Portal:数学）。

[sqrtexp-1] Kneser, H. (1950). “Reelle analytische Lösungen der Gleichung φ(φ(x)) = e^x und verwandter Funktionalgleichungen”. Journal fur die reine und angewandte Mathematik 187: 56–67.

[2] Jeremy Gray and Karen Parshall (2007) Episodes in the History of Modern Algebra (1800–1950), American Mathematical Society, ISBN 978-0-8218-4343-7

[schr-3] Schröder, E. (1870). “Ueber iterirte Functionen”. Mathematische Annalen 3 (2): 296–322. doi:10.1007/BF01443992.

[4] Szekeres, G. (1958). “Regular iteration of real and complex functions”. Acta Mathematica 100 (3–4): 361–376. doi:10.1007/BF02559539.

[5] Curtright, T.; Zachos, C. (2011). “Approximate solutions of functional equations”. Journal of Physics A 44 (40): 405205. doi:10.1088/1751-8113/44/40/405205.

[6] Curtright, T.L. Evolution surfaces and Schröder functional methods.

[1]

[2]

[3]

[4]

[5]

[6]

例

関連項目

参考文献