合流点 (統計学)
表示
統計学や因果グラフにおいて、ある変数が2つ以上の変数から因果的な影響を受けている場合、その変数は合流点(ごうりゅうてん、コライダー、Collider)と呼ばれる。 この名称は、グラフィカルモデルにおいて、合流点につながる変数からの矢印が、合流点であるノード上で「衝突」しているように見えること反映している[1]。逆フォーク(inversed fork)と呼ばれることもある[2]。
概要
[編集]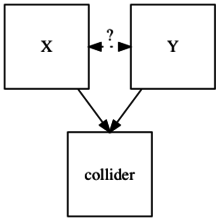
合流点に影響を与える因果変数同士は、相互に関連しているとは限らない[3]。
合流点に影響を与える因果変数同士の関連性を、合流点がブロックする[4][5][6]。合流点は、合流点に影響を与える因果変数同士の関連性を無条件に生成するわけではない。
回帰分析、層別化、実験計画、標本選択において、合流点に基づいて条件付けすると、XとYとの間に非因果的な関係が生まれる(バークソンのパラドックス)。因果グラフの用語を用いると、合流点で条件付けすることにより、 XとYとの間のパスが開く。これにより、XとYとの間の因果関係を推定するときにバイアスがかかり、因果関係がなくても関連性が生じる可能性がある。そのため、合流点は、因果理論を検証する試みを台無しにしてしまう。
合流点(Collider)はときどき、交絡変数(Confounder)と混同される。合流点とは逆に、因果関係を推定する際には交絡変数をコントロールする必要がある。
関連項目
[編集]脚注
[編集]- ^ Hernan, Miguel A.; Robins, James M. (2010), Causal inference, Chapman & Hall/CRC monographs on statistics & applied probability, CRC, p. 70, ISBN 978-1-4200-7616-5
- ^ Julia M. Rohrer (2018年7月2日). “Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data”. PsyArXiv. doi:10.31234/osf.io/t3qub. 2021年10月22日閲覧。
- ^ Ali, R. Ayesha; Richardson, Thomas S.; Spirtes, Peter; Zhange, Jiji (2012). “Towards characterizing Markov equivalence classes for directed acyclic graphs with latent variables”. Proceedings of the Twenty-First Conference on Uncertainty in Artificial Intelligence (UAI2006): 10–17. arXiv:1207.1365 14 December 2020閲覧。.
- ^ Greenland, Sander; Pearl, Judea; Robins, James M. (January 1999), “Causal Diagrams for Epidemiologic Research”, Epidemiology 10 (1): 37–48, doi:10.1097/00001648-199901000-00008, ISSN 1044-3983, OCLC 484244020, PMID 9888278
- ^ Pearl, Judea (1986). “Fusion, Propagation and Structuring in Belief Networks”. Artificial Intelligence 29 (3): 241–288. doi:10.1016/0004-3702(86)90072-x.
- ^ Pearl, Judea (1988). Probabilistic reasoning in intelligent systems: networks of plausible inference. Morgan Kaufmann
