バブルソート
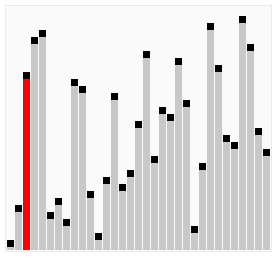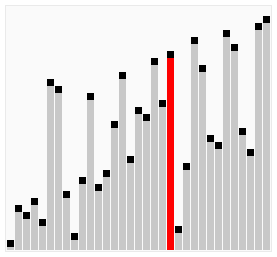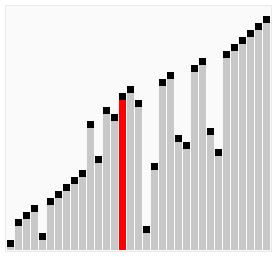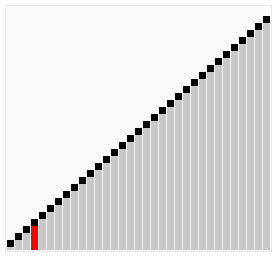 バブルソートがどのように動作するかの視覚的な説明 | |
| クラス | ソート |
|---|---|
| データ構造 | 配列 |
| 最悪計算時間 | |
| 最良計算時間 | |
| 平均計算時間 | |
| 最悪空間計算量 | auxiliary |
バブルソート(英: bubble sort)は、隣り合う要素の大小を比較しながら整列させるソートアルゴリズム。
アルゴリズムが単純で実装も容易である一方、最悪時間計算量は O(n2) と遅いため、一般にはマージソートやヒープソートなど、より最悪時間計算量の小さな(従って高速な)方法が利用される。
また、安定な内部ソートであり、並列計算との親和性が高いという利点もある。
基本交換法、隣接交換法[1]あるいは単に交換法とも呼ばれる。「バブルソート」という呼称自体はケネス・アイバーソンの1962年の著書 “A Programming Language” に由来すると考えられる[2]。
アルゴリズム
[編集]
全ての要素に関して、隣接する要素と比較し順序が逆であれば入れ替える。これを要素数-1回繰り返すことでソートを行う。なおこの繰り返しは、入れ替えが起こらなくなった時点で(それ以降は何度繰り返しても変化が起こらなくなるので)中断することができる。
この「全ての要素に関して」において、全ての要素に関して比較交換が行なわれるならば順序を問わない特徴を持つ(安定ソート)。この特徴により、比較交換順序を調整することで効率化されたアルゴリズムが多数派生している。そのため他の様々なソートアルゴリズムの基礎として一度は学ばされるアルゴリズムとなっている。
例えば前記の特徴によりバブルソートは並列処理と親和性が高く、比較交換器を潤沢に用いることで比較交換順序を調整したハードウェア実装では時間計算量はO(n)になる。この並列処理向けに比較交換順序を調整したアルゴリズムとして奇偶転置ソートがある。
また特にソフトウェアで実装される場合には一般に先頭から順に順次処理されるものなので、逆に先頭から順に順次処理されることを利用して不要なことが自明な比較交換をしないように効率化することは有効かつ直感的であり、この効率化されたアルゴリズムをもってバブルソートと呼ぶ場合もある。さらに、比較交換順序を逆順にすることで自明な比較交換を検出し易くしたアルゴリズムに挿入ソートがあり、効率化されたバブルソートは簡単な変更で容易に挿入ソートにできることから、ソートのソフトウェア実装としてバブルソートを選択する根拠はなく、学習専用の非効率的なアルゴリズムと考えられているのが現状である。
なお、係る派生したアルゴリズムが隣接する要素と比較交換以外の比較や交換を行なうことで効率化を図っている場合、安定という特徴を失う。
以下では、前記の自明な比較交換をしないように効率化されたバブルソートに関して解説する。
要素の1番目と2番目を比較し、順番が逆であれば入れ換える。次に2番目と3番目を比較して入れ換える。これを最後まで行うと、最後の数だけが最小または最大の数として確定するので、確定していない部分について1つずつ減らしながら繰り返す。
procedure bubbleSort( A : list of sortable items ) defined as:
for each i in 1 to length(A) - 1 do:
for each j in 2 to length(A) - i + 1 do:
if A[ j ] < A[ j - 1 ] then
swap( A[ j ], A[ j - 1 ] )
end if
end for
end for
end procedure
動作例
[編集]
初期データ: 6 5 3 1 8 7 2 4
初期データ: 8 4 3 7 6 5 2 1
結果が確定した部を太字でしめすと、
| 4 | 3 | 7 | 6 | 5 | 2 | 1 | 8 | (1回目の外側ループ終了時 交換回数:7) |
| 3 | 4 | 6 | 5 | 2 | 1 | 7 | 8 | (2回目の外側ループ終了時 交換回数:5) |
| 3 | 4 | 5 | 2 | 1 | 6 | 7 | 8 | (3回目の外側ループ終了時 交換回数:3) |
| 3 | 4 | 2 | 1 | 5 | 6 | 7 | 8 | (4回目の外側ループ終了時 交換回数:2) |
| 3 | 2 | 1 | 4 | 5 | 6 | 7 | 8 | (5回目の外側ループ終了時 交換回数:2) |
| 2 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | (6回目の外側ループ終了時 交換回数:2) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | (7回目の外側ループ終了時 交換回数:1) |
交換回数の合計:7+5+3+2+2+2+1=22
解析
[編集]
「比較回数」は、高々n(n-1)/2回。交換回数は、元のデータ列によって異なるが、一回のスキャンで平均n/2回なので、全体では平均n(n-1)/4回。(O(n2))
バブルソートでは、大きな数が列の始めに位置していても問題ないが、右図のように列の後のほうに位置している小さな数は列の始めのほうに移動してくるのに時間がかかる。(上述の動作例中の"1"がまさにそのパターン)これを改良するために、シェーカーソートやコムソートが提案された。



