符号付き距離関数

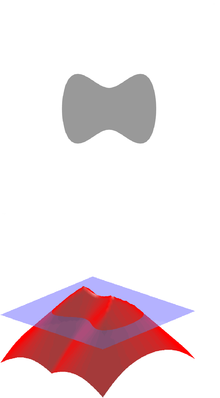
符号付き距離関数（ふごうつききょりかんすう、英語: signed distance functionまたは英語: oriented distance function、SDF）は、与えられた点xから距離空間における集合Ωの境界までの垂直距離（英語版）である。xがΩの内部にあるかどうかによって符号が決まる。この関数は、Ωの内部の点xでは正の値を持ち、Ωの境界に近づくにつれて値が減少し、符号付き距離関数がゼロになる場所でΩの境界に達し、Ωの外部では負の値を取る^[1]。負の値を内部、正の値を外部とする規約が採用されることもある^[2]。

定義

$Ω$ を距離空間 $X$ の部分集合とし、 $\partial \Omega$ をその境界とする。 $X$ の点 $x$ と $X$ の部分集合 $\partial \Omega$ との距離は自然に次のように定義される。 $d(x,\partial \Omega )=\inf _{y\in \partial \Omega }d(x,y),$ ここで $\inf$ は下限を表す。

点 $x$ から $X$ の $\Omega$ までの符号付き距離関数は次のように定義される。 $f(x)={\begin{cases}d(x,\partial \Omega )&{\text{if }}x\in \Omega \\-d(x,\partial \Omega )&{\text{if }}\,x\notin \Omega .\end{cases}}$

ユークリッド空間における特性

Ωがユークリッド空間Rⁿの区分的に滑らかな境界を持つ部分集合である場合、符号付き距離関数はほとんど至る所で微分可能であり、その勾配はアイコナール方程式を満たす。

$|\nabla f|=1$

Ωの境界がk ≥ 2でC^k（滑らかな関数#滑らかさの分類を参照）である場合、dはΩの境界に十分に近い点でC^kである。^[3] 特に、境界f上においては

$\nabla f(x)=N(x)$

を満たす。ここでNは内向きの法ベクトル場である。したがって、符号付き距離関数は法ベクトル場の微分可能な拡張である。特に、Ωの境界における符号付き距離関数のヘッセ行列は形作要素（英語版）を与える。

さらに、Ωの境界に十分に近くfがその上で2回連続的に微分可能である領域Γに対し、符号付き距離関数と最も近い境界点の変数変換のヤコビアンには形作用素W_xを用いた公式が存在する。特に、T(∂Ω, μ)がΩの境界から距離μ以内の点の集合（つまり、半径μの管状近傍）であり、gがΓ上の絶対可積分関数である場合、

$\int _{T(\partial \Omega ,\mu )}g(x)\,dx=\int _{\partial \Omega }\int _{-\mu }^{\mu }g(u+\lambda N(u))\,\det(I-\lambda W_{u})\,d\lambda \,dS_{u}$

が成り立つ。ここで $det$ は行列式を示し、dS_uは面積分を取ることを示す^[4]。

アルゴリズム

符号付き距離関数を計算するためのアルゴリズムには、効率的なファストマーチング法（英語版）、ファストスウィーピング法（英語版）^[5] およびより一般的なレベルセット法（英語版）がある。

ボクセルレンダリング向けには、タクシー幾何学でSDFを計算するために範囲総和表（英語版）を使用する高速アルゴリズムが存在する^[6]。

応用

符号付き距離関数が利用される分野の例としては、リアルタイムレンダリング（英語版）^[7]、SDFレイマーチング（英語版）、コンピュータビジョンなどがある^[8]^[9]。

SDFは2000年代半ばからレイマーチングの実装においてリアルタイムレンダリングにおけるオブジェクトのジオメトリを記述するために使用され始めた。2007年にはValveが、SDFを使用して大きなピクセルサイズ（または高DPI）の滑らかなフォントをGPUアクセラレーションでレンダリングしている^[10]。Valveの手法は（連続的な）ベクタ空間での問題を解く計算複雑性を避けるためにラスタ空間で実行されるため完璧ではなく、レンダリングされたテキストは角が丸まってしまうことが多い。2014年には、en:Behdad Esfahbodによって改良された手法が発表された。BehdadのGLyphyはフォントのベジエ曲線をスプライン曲線で近似し、グリッドベースの離散化手法（遠すぎる点をカリングする）によってリアルタイムで実行する^[11]。

複数のオブジェクトをレンダリングする際のピクセルの侵入エラーを最小化するための損失関数としてSDFの修正版が使われている^[12]。オブジェクトに属さないピクセルに対して、それがレンダリング時にオブジェクトの外側にある場合はペナルティは課さず、内部にある場合はその距離に比例した正の値を課すというものである。

$f(x)={\begin{cases}0&{\text{if }}\,x\in \Omega ^{c}\\d(x,\partial \Omega )&{\text{if }}\,x\in \Omega \end{cases}}$

2020年には、FOSSのゲームエンジンGodot 4.0がSDFベースのリアルタイムGI（SDFGI）を実装した^[13]。既存のボクセルベースのGIよりパフォーマンスは劣るものの^[14]、広い空間に適用可能であるためオープンワールドゲームの開発に用いることができる^[13]。

2023年には、すべてのUI要素をGPUを使用して描画する「GPUI」UIフレームワークがリリースされ、120 fpsでレンダリングを行うZedコードエディタを開発したと発表された。このフレームワークは多くの部分でSDFを使用し、Inigo QuilezによるSDF向け幾何学図形プリミティブ、Evan Wallace（Figmaの共同創設者）のSDFにおける近似ガウシアンぼかし、および丸みを帯びた長方形のSDFを利用している^[15]。

脚注

^ Chan, T.; Zhu, W. (2005). Level set based shape prior segmentation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2005.212。
^ Malladi, R.; Sethian, J.A.; Vemuri, B.C. (1995). “Shape modeling with front propagation: a level set approach”. IEEE Transactions on Pattern Analysis and Machine Intelligence 17 (2): 158–175. doi:10.1109/34.368173.
^ Gilbarg & Trudinger 1983, Lemma 14.16.
^ Gilbarg & Trudinger 1983, Equation (14.98).
^ Zhao Hongkai. A fast sweeping method for eikonal equations. Mathematics of Computation, 2005, 74. Jg., Nr. 250, S. 603-627.
^ Nilsson, Tobias (2019年). “Optimization Methods for Direct Volume Rendering on the Client Side Web”. Digitala Vetenskapliga Arkivet. 2022年7月8日閲覧。
^ Tomas Akenine-Möller; Eric Haines; Naty Hoffman (6 August 2018). Real-Time Rendering, Fourth Edition. CRC Press. ISBN 978-1-351-81615-1
^ Perera, S.; Barnes, N.; He, X.; Izadi, S.; Kohli, P.; Glocker, B. (January 2015). “Motion Segmentation of Truncated Signed Distance Function Based Volumetric Surfaces”. 2015 IEEE Winter Conference on Applications of Computer Vision. pp. 1046–1053. doi:10.1109/WACV.2015.144. ISBN 978-1-4799-6683-7
^ Izadi, Shahram; Kim, David; Hilliges, Otmar; Molyneaux, David; Newcombe, Richard; Kohli, Pushmeet; Shotton, Jamie; Hodges, Steve et al. (2011). “KinectFusion”. Proceedings of the 24th annual ACM symposium on User interface software and technology. UIST '11. New York, NY, USA: ACM. pp. 559–568. doi:10.1145/2047196.2047270. ISBN 9781450307161
^ Green, Chris (2007). “Improved alpha-tested magnification for vector textures and special effects”. ACM SIGGRAPH 2007 courses. pp. 9–18. doi:10.1145/1281500.1281665. ISBN 9781450318235
^ Behdad Esfahbod. GLyphy: high-quality glyph rendering using OpenGL ES2 shaders [linux.conf.au 2014]. YouTube. 2021年12月11日時点のオリジナルよりアーカイブ。 Source Code
^ Jiang, Wen; Kolotouros, Nikos; Pavlakos, Georgios; Zhou, Xiaowei; Daniilidis, Kostas (15 June 2020). "Coherent Reconstruction of Multiple Humans from a Single Image". arXiv:2006.08586 [cs.CV]。
^ ^a ^b “Godot 4.0 gets SDF based real-time global illumination” (英語). Godot Engine. 2024年5月28日閲覧。
^ Godot Engine. “Signed distance field global illumination (SDFGI)”. 2024年5月29日閲覧。
^ “Leveraging Rust and the GPU to render user interfaces at 120 FPS - Zed Blog”. Zed (7 March 2023). 2024年5月28日閲覧。

定義

ユークリッド空間における特性

アルゴリズム

応用

脚注

関連項目