自己エネルギー

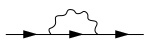
電子の自己エネルギーを表すファインマン・ダイアグラム。波線は光子、実線は電子を表す。
自己エネルギー(じこエネルギー、英: self-energy)とは、粒子が自分自身の作り出す場との相互作用によって生じるエネルギーのことである。
概要
[編集]場の量子論や物性物理学において、相互作用がある場合のグリーン関数(伝播関数)を摂動論で計算する際、ウィックの定理(またはブロッホ=ドミニシスの定理)によってファインマンダイアグラムを使うことができる。ファインマンダイアグラムの自己エネルギー部分とは、ダイアグラムの他の部分と2本の粒子線だけで繋がっているような部分の総称である。
実際に摂動展開をダイアグラムで書き下してみると、一部分が同じ形をしているダイアグラムがくりかえし表れることが分かる。ここで既約自己エネルギー部分(irreducible self energy)またはプロパーな自己エネルギー部分(proper self energy)を、1本の粒子線を切断するだけでは2つの部分に分離することができないようなダイアグラムで表される自己エネルギー部分と定義する。すると摂動展開は、既約自己エネルギー部分を、相互作用を含むグリーン関数を太い矢印、自由粒子のグリーン関数を細い矢印として、次のようなダイアグラムで表される。
これを数式で表したものはダイソン方程式と呼ばれる。既約自己エネルギーを、相互作用を含むグリーン関数を、自由粒子のグリーン関数をとすると、ダイソン方程式は次のように書ける。
場の量子論では相互作用によるエネルギー(分散関係)の変化は質量変化を表すため、自己エネルギーを質量演算子と呼ぶこともある。
物性物理学
[編集]グリーン関数はある時刻で生成した粒子が、その後の時刻でどの程度存在するかという期待値を意味する。相互作用のない場合、生成した粒子の寿命は無限大であり、スペクトル関数はデルタ関数型となる。
一方で相互作用が与えられると、粒子の寿命やスペクトル関数に変化が生じる。相互作用の衣を着た粒子を準粒子という。相互作用があるとスペクトル関数に広がりが生じ、自己エネルギーの虚部はその広がりを表す。また相互作用によってグリーン関数は減衰し、自己エネルギーの虚部の逆数は準粒子の寿命を表す。これは、相互作用があると粒子が生成した状態はもはや系の固有状態(定常状態)ではなくなり、別の状態に遷移してしまうことを意味する。スペクトル関数のピーク位置も相互作用によってシフトし、自己エネルギーの実部はそのエネルギーシフト、つまり相互作用による準粒子のエネルギー補正を表す。その他にも準粒子の有効質量なども自己エネルギーから計算することができる。
量子電磁力学
[編集]場の量子論における自己エネルギーは、粒子が自ら仮想粒子を放出し吸収する過程、及び、その過程により増加する粒子の質量エネルギーである。量子電磁力学(QED)においては、電子や陽電子のようなフェルミ粒子が自ら光子を放出し吸収することで、フェルミ粒子の質量が増加する過程を表す。光子やグルーオンのようなゲージ粒子、更には中間子のようなボーズ粒子の場合も自己エネルギーは定義でき、これらは一般に真空偏極と呼ばれる。
四元運動量を持つフェルミ粒子が光子を放出し、吸収する過程を考える。フェルミ粒子の自己エネルギー は、1粒子既約な(1つの伝播関数を切断して2つ以上に分離できないような)全てのダイアグラムを足し上げたものとして定義される。
ここでダイアグラムにはループの両端に実線が便宜的に引かれているが、自己エネルギーとして定義されているのは実線+波線のループ部分のみであることに注意。この式の高次の項には2ループ以上のループを含む1粒子既約なダイアグラムが存在する。ファインマンルールを用いて1ループ積分を書き下すと、入射するフェルミ粒子の運動量をp、仮想光子の運動量をkとして
となる。やはファインマンのスラッシュ記法と呼ばれる。この式は仮想光子の運動量kについての積分であるので、フェルミ粒子の運動量pのみを変数とする関数となっている。さらにこの積分は、分子がd4k、分母がk3に比例するから、kについての1次発散を含むことが分かる。
ファインマン伝播関数
[編集]フェルミ粒子の2点相関関数、すなわちファインマン伝播関数に対して、自己エネルギーによる補正を加えるためには、全ての可能なダイアグラムを足し上げればよい。
ここで、最右辺の第1項が自由な伝播関数、それ以降の項は自己エネルギーの両端にフェルミ粒子の伝播関数がついた1粒子既約、2粒子既約…のダイアグラムを表す。この式はファインマンルールを用いて計算され、フェルミ粒子の運動量をp、裸の質量をm0とすると、
となる。この式は、元々は裸の質量m0の位置にあった伝播関数の極が、自己エネルギーによってシフトしていることを表している。従って、物理的な質量mを求めるためには、方程式
を解けばよく、質量のシフトは
と表せる。実際に自己エネルギーから質量シフトを計算すると、運動量カットオフΛと微細構造定数αを用いて、
となり、対数の紫外発散となっていることが分かる。
参考文献
[編集]- M.E. Peskin; D.V. Schroeder (1995). An Introduction To Quantum Field Theory. Westview Press. ISBN 978-0201503975
















![{\displaystyle \left.\left[p\!\!/-m_{0}-\Sigma (p\!\!/)\right]\right|_{p\!\!/=m}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e1788bbc6d77c9e519a263496a0e441ebd037da)

