近代三角形幾何学

エミール・ルモワーヌ (1840–1912)

数学において、近代三角形幾何学（きんだいさんかくけいきかがく、 英語: modern triangle geometry, new triangle geometry）は19世紀後半から急激に発展した、三角形の性質に関連する研究の体系である。

三角形の諸性質はユークリッドの時代から研究され続けてきた。ユークリッド原論では、三角形の重要な心として重心（幾何中心）、内心、外心、垂心が記述されている。17世紀のブレーズ・パスカル、ジョバンニ・チェバ、18世紀のレオンハルト・オイラー、19世紀のカール・フォイエルバッハなど多くの数学者により三角形の研究が成された。1873年のエミール・ルモワーヌの論文「On a remarkable point of the triangle」はネイサン・アルトシュラ―・コートによって

「laid the foundations...of the modern geometry of the triangle as a whole」

と評価されている。 ルモワーヌの著作を出版したAmerican Mathematical Monthlyは

「To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry」

と宣言している 。ルモワーヌのこの論文は、19世紀の最後の四半世紀以後の三角形の性質への関心を非常に高めることとなった。1914年に出版された Klein's Encyclopedia of Mathematical Sciencesは100ページを超える三角形幾何学の記事で、このような高まりを物語っている一例である。

近年、「new triangle geometry」は三角形に関する図形などの対象を指すことが多い。例えばルモワーヌ点、ブロカール円、ルモワーヌ線が挙げられる。後に、幾何的な変換から派生した結果をまとめる理論も開発された。この理論の発展から 「new triangle geometry」は単に対象を指す言葉ではなく、対象の分類や研究の方法に対しても使われる言葉になった。1887年のヨーロッパとアメリカで使われた幾何学の教科書「Teaching new geometrical methods with an ancient figure in the nineteenth and twentieth centuries」では

「Being given a point M in the plane of the triangle, we can always find, in an infinity of manners, a second point M' that corresponds to the first one according to an imagined geometrical law; these two points have between them geometrical relations whose simplicity depends on the more or less the lucky choice of the law which unites them and each geometrical law gives rise to a method of transformation a mode of conjugation which it remains to study」

との記述がある。

しかし、この高まりは一度収束して、20世紀まで、完全に姿を見せなかった。 エリック・テンプル・ベルの「Development of Mathematics」内で、三角形幾何学についてこのような言及がある。

「The geometers of the 20th Century have long since piously removed all these treasures to the museum of geometry where the dust of history quickly dimmed their luster.」

フィリップ・J・デイヴィスは三角形幾何学の衰退に以下のようないくつかの理由があると述べた。

• 専門性が低く初等的だと感じる
• 研究方法の可能性の枯渇
• 視覚的な複雑さ
• 解析的な手法が優先されたこと
• タイル張り、フラクタル、グラフ理論など他の視覚的な分野との競合

近代的なコンピュータの登場は、三角形幾何学の復興に大きな影響を与えた。熱心な幾何学者らによって、三角形幾何学は再び活発な分野となった。 その典型例として、クラーク・キンバリングの三角形の心をまとめたウェブサイト「Encyclopedia of Triangle Centers」や、Bernard Gibertの三角形の三次曲線をまとめたウェブサイト、「Catalogue of Triangle Cubics」が挙げられる。他にも、フロリダ・アトランティック大学のパウル・ヨウによるジャーナル「Forum Geometricorum」が近代の三角形幾何学の発展に貢献している。

ルモワーヌ幾何学

ルモワーヌ点

△ABCの重心をGとする。AG,BG,CGをそれぞれA,B,Cの角の二等分線で鏡映した線は類似中線（Symmedian）と呼ばれる。3本の類似中線は共点で、この点を類似重心（ルモワーヌ点、グリーブ点）という。△ABCのそれぞれの辺をa,b,cとして、類似重心の重心座標はa²:b²:c²である。 類似重心は「one of the crown jewels of modern geometry」と言われている。 この点に関する文献にはジョン・キース・ステュアート・マッケイの「history of the symmedian point」などがある。

類似重心と重心のような関係は等角共役として一般化されている。△ABCと点Pについて、AP,BP,CPをそれぞれA,B,Cの角の二等分線で鏡映した直線は、一点で交わる。これをPの等角共役点という。

ルモワーヌ円

類似重心を通り各辺に平行な直線と他二辺の交点、計6点は同一円上にある。この円を第一ルモワーヌ円という。円の中心は、類似重心と外心の中点である。また、この性質も一般化されている（三角形の円錐曲線を参照）

類似重心を通り各辺に逆平行な直線と、他二辺の交点も共円である。この円を第二ルモワーヌ円またはcosine circleという。中心は類似重心である。

ルモワーヌ軸

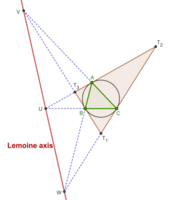
△ABCとその接線三角形（類似重心の反チェバ三角形）の配景の軸をルモワーヌ軸という。これは類似重心の三線極線である。

• 
  類似中線 (赤)と類似重心L.
• 
  第一ルモワーヌ円
• 
  第二ルモワーヌ円
• 
  ルモワーヌ軸

初期の近代三角形幾何学

ルモワーヌの論文が発表されたあとの三角形幾何学に関する発見を挙げる（ 1910年のウィリアム・ゲラトゥリの書籍と1929年のロガー・アーサー・ジョンソンの書籍に基づく）。

Poristic triangles

内接円と外接円を共有する三角形はPoristic trianglesと呼ばれる。オイラーの定理によれば、外接円、内接円の半径をそれぞれR,rとして外心と内心の距離の二乗はR²-2Rrで表される。Poristic trianglesに対して、重心などいくつかの点の軌跡は円または点となる（ヴァイルの定理、ポンスレの閉形定理も参照）。

シムソン線

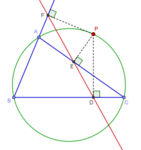
△ABCの外接円上の点Pについて、Pから各辺に降ろした垂線に足は共線である。この線はシムソン線と呼ばれる。

垂足三角形と反垂足三角形

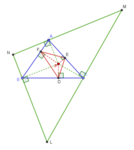
点Pから各辺に降ろした垂線の足が成す三角形をPの垂足三角形という。A,B,Cを通り、それぞれAP,BP,CPに垂直な直線の成す三角形を反垂足三角形という。 Pの垂足三角形とQの反垂足三角形が相似の位置にある且つ、Qの垂足三角形とPの反垂足三角形が相似の位置にある場合、P,Qはcounter pointsと呼ばれる。

直極点

任意の直線lについて、A,B,Cからlに降ろした垂線の足をP,Q,Rとする。P,Q,Rを通るBC,CA,ABの垂線は一点で交わる。これをlの直極点と言う。近代の三角形幾何学の文献には直極点を扱ったものが多く存在する。

ブロカール点

BC,CA,ABに接して、それぞれC,A,Bを通る円は一点で交わる。同様にB,C,Aを通る円も共点である。この2点をブロカール点という。$\Omega ,\Omega ^{\prime }$で表される場合が多い。接弦定理から示すことができる。また、この時∠PBC,PCA,PABは等しい。この角をブロカール角といい、$\omega$で表される。ブロカール角に関して、以下の等式が成り立つ。

$\cot \omega =\cot A+\cot B+\cot C.$

ブロカール点、ブロカール角は多くの興味深い性質を持つ。

画像

• 
  内接円I(r)と外接円Ｏ(R)を共有する三角形△ABC,A'B'C'
• 
  Pのシムソン線
• 
  Pの垂足三角形DEFと反垂足三角形LMN
• 
  lの直極点
• 
  第一ブロカール点

現代の近代三角形幾何学

三角形の心

20世紀のもっとも重要な三角形幾何学の概念の一つに三角形の中心が挙げられる。1994年にクラーク・キンバリングによって導入され、非常に多くの点が統一的に扱われるようになった。 この概念の導入後は、三角形の中心なしでは三角形の諸性質は完結しなくなった。

三角形の心の定義

3つの実数a,b,cについて関数fを以下の様に定義する。

• 斉次性: f(ta,tb,tc) = tⁿ f(a,b,c) ( nは任意の定数で、tはすべての正の実数）
• 2,3つ目の変数に対する対称性: f(a,b,c) = f(a,c,b)

fが零関数でない且つ上の二条件を満たすならばそれをtriangle center functionと呼ぶ。a,b,cが三角形の各辺の長さであるならば、重心座標または三線座標において表記された点f(a,b,c): f(b,c,a) : f(c,a,b)を三角形の心という。この定義によれば傍心やブロカール点は三角形の中心でない。

クラーク・キンバリングは、三角形の心をまとめた Encyclopedia of Triangle Centersを運営している。このウェブサイトには2024年現在、62000個程度 の三角形の心が登録されている。

Central line

現代の三角形幾何学のもう一つの重要な概念にCentral lineが挙げられる。Central lineは三角形の心と密接にかかわっている。

central lineの定義

△ABCにおいて、三線座標(x : y : z)を変数とし、以下の式で表される直線をCentral lineという。

$f(a,b,c)x+g(a,b,c)y+h(a,b,c)z=0$

ただしf(a,b,c): g(b,c,a) : h(c,a,b)は三角形の中心である。

幾何的なcentral lineの作図

• 点Xの等角共役点をYとする。
• それぞれチェバ線AY,BY,CYとBC,CA,ABの交点の成す三角形（チェバ三角形）を△A'B'C' とする。
• △ABCと△A'B'C' の配景の軸がYの三線極線、XのCentral lineである。

三角形の円錐曲線

三角形の円錐曲線は三角形に対して定義される平面円錐曲線 である。代表的なものに外接円と内接円、シュタイナー楕円、キーペルト双曲線がある。他に2点と1辺の組に対して定義されるアーツ放物線 、いくつかの円錐曲線の集合である ホフスタッター楕円やイフ円錐曲線などもある。「Triangle conics」と言う語に正確な定義はされていないがMathWorldには42個の「Triangle conics」と書かれた項が存在する。

• 
  シュタイナー外接楕円
• 
  アーツ放物線
• 
  キーペルト双曲線

三角形の三次曲線

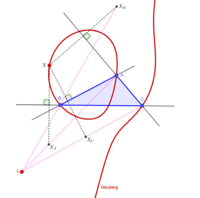
三次曲線は三角形の研究に、主に軌跡を調べる場合などに自然に出現する。 例えば、点Pを三角形の各辺BC,CA,ABで鏡映した点P_A,P_B,P_Cについて、AP_A,BP_B,CP_Cが共点であるとき、Pの軌跡はノイベルグ三次曲線と呼ばれる三次曲線を成す。三角形の三次曲線はBernard Gibertの 運営するCatalogue of Triangle Cubicsに1200個程度登録されており、重心座標による方程式や、軌跡などのさまざまな情報が記載されている。

• 
  ノイベルグ三次曲線 (K001)
• 
  McCay cubic (K003)
• 
  Tucker cubic (K011)

三角形幾何学とコンピュータ

20世紀、コンピュータの発展は三角形幾何学の発展に大きな影響を与えた。例えばGeoGebraやGeometer's Sketchpadが挙げられる。

フィリップ・J・デイヴィスはコンピュータが三角形幾何学にどのように影響したか以下の様に言及している。

Computers have been used to generate new results in triangle geometry. A survey article published in 2015 gives an account of some of the important new results discovered by the computer programme "Dircoverer". The following sample of theorems gives a flavor of the new results discovered by Discoverer.

• Theorem 6.1 Let P and Q are points, neither lying on a sideline of triangle ABC. If P and Q are isogonal conjugates with respect to ABC, then the Ceva product of their complements lies on the Kiepert hyperbola.
• Theorem 9.1. The Yff center of congruence is the internal center of similitude of the incircle and the circumcircle with respect to the pedal triangle of the incenter.
• The Lester circle is the circle which passes through the circumcenter, the nine-point center and the outer and inner Fermat points. A generalised Lester circle is a circle which passes through at least four triangle centers. Discoverer has discovered several generalized Lester circles.

Sava Grozdev, Hiroshi Okumura, Deko Dekovなどはユークリッド幾何学に特化した百科事典の運営を行っている。

参考文献

• John Mackay (1896). “Symmedians of a Triangle and their Concomitant Circles”. Proceedings of the Edinburgh Math. Soc. XIV: 37–103. https://www.cambridge.org/core/services/aop-cambridge-core/content/view/323CD668423E3D558C600F91D26A7816/S0013091500031758a.pdf/symmedians-of-a-triangle-and-their-concomitant-circles.pdf 2022年1月7日閲覧。. 
• William Gallatly (1910). The Modern Geometry of the Triangle. London: Francis Hodgson. https://archive.org/details/cu31924001522782 2022年1月4日閲覧。 
• Ross Honsberger (1995). Episodes in Nineteenth and Twentienth Century Euclidean Geometry. Mathematical Association of America 
• Roger A Johnson (31 August 2007). Advanced Euclidean Geometry. Dover Publications Inc.. ISBN 978-0486462370 
• H S M Coexter (5 September 1996). Geometry Revisited. Mathematical Association of America. ISBN 0883856190 
• Altshiller-Court, Nathan (1952). College geometry; an introduction to the modern geometry of the triangle and the circle. New York: Barnes & Noble. https://archive.org/details/collegegeometryi00alts/page/n3/mode/2up 2022年1月10日閲覧。 
• Kimberling, C (1998). “Triangle Centers and Central Triangles”. Congr. Numer.: 1–295. 
• Paul Yiu (December 2012). Introduction to the Geometry of the Triangle. Department of Mathematics Florida Atlantic University. http://math.fau.edu/Yiu/YIUIntroductionToTriangleGeometry121226.pdf 2022年1月5日閲覧。 
• Scott, Charlotte Angas (1894). An introductory account of certain modern ideas and methods in plane analytical geometry. London: Macmillan and Co. https://archive.org/details/anintroductorya04scotgoog/page/n6/mode/2up 2022年1月10日閲覧。