シュレーディンガー方程式
この項目「シュレーディンガー方程式」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:英語版 "Schrödinger equation") 修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。ノートページや履歴も参照してください。(2013年4月) |
原文と比べた結果、この記事には多数の(または内容の大部分に影響ある)誤訳があることが判明しています。情報の利用には注意してください。 |
シュレーディンガー方程式(シュレーディンガーほうていしき、Schrödinger equation)とは、量子力学における純粋状態(状態ベクトルまたは波動関数で表される)の時間発展を記述する方程式である。1926年にオーストリアの物理学者エルヴィン・シュレーディンガーが量子力学の一形式である波動力学の基礎方程式として提案した。
古典力学において、運動方程式はニュートン力学における運動の第2法則であり、同等の公式にオイラー=ラグランジュ方程式やハミルトン力学がある。これらの公式は機械の動作を解明するために使われたり、初期設定や機械の構成の上で、物理系が各時間に対してどのように作用をするか数学的に予想するために使われる。
量子力学において、ニュートンの法則の類似物が、 量子系(通常原子や分子、亜原子粒子など、自由か束縛されているか局所的なもの )に対するシュレーディンガー方程式である。単純な代数方程式ではないが、(一般には)線型偏微分方程式である。微分方程式は系の波動関数を表し、量子状態や量子ベクトルなどと呼ばれる。
コペンハーゲン解釈(量子力学の標準的な解釈)では、波動関数は物理系に与えることができる最も完璧な記述である。シュレーディンガー方程式の解答は分子、原子、亜原子粒子のみを説明するものではなく、微視的な系や、宇宙全体でさえも可能である。
運動の第2法則のように、シュレーディンガー方程式は、ヴェルナー・ハイゼンベルクの行列力学や、リチャード・P・ファインマンの経路積分のような他の公式に数学的に変換ができる。 第2法則と同じように、シュレーディンガー方程式は相対性理論にとって不都合な方法、行列力学のように深刻ではない、経路積分にとっては完全に存在しない問題で時間を説明する。シュレーディンガー方程式は標準的な波動関数や、代わりに分子の運動量とド・ブロイ波における分子に関連する波の波長との関係の部分微分から求められる。
方程式
シュレーディンガー方程式
状態ベクトルに対するシュレーディンガー方程式は
と表される(時間依存型シュレーディンガー方程式)。ここで、は量子系の波動関数、iは虚数単位、はディラック定数、は系の全力学的エネルギーを表す「ハミルトニアン(ハミルトン演算子)」を表す。ハミルトニアンは与えられた波動関数の全エネルギーを表すエルミート演算子であり、考えている系に応じて異なる形を取る。対応する古典系のハミルトニアンを正準量子化する事によって得られることが多い。正準量子化の結果、次のようにベクトル表示しない表現となる。ベクトル表示するか否かは書籍によって色々である。
量子論では時間発展しても確率が保存されなければならない。つまりどんな場合でもすべての確率の合計は100%にならなければならない。この事とボルンの規則による確率の求め方(ベクトルの内積で確率は求められる)より、状態ベクトルの時間発展はユニタリ変換でなければならないことがわかる。シュレーディンガー方程式を解くことで、「状態ベクトルの時間発展はユニタリ変換である」ということが導かれる。よって量子系の時間発展についての基本的な要請(原理)は、シュレーディンガー描像で記述する場合は、このシュレーディンガー方程式を採用して出発することが多い。しかし他にも「時間発展演算子が満たすべき条件」を基本的な要請として出発することもある[1]。

最も有名な例は電場中(磁場もある時にはパウリ方程式を用いる)で運動する粒子に対する非相対論的シュレーディンガー方程式である。
時間依存型シュレーディンガー方程式 (非相対論的単一粒子)
mは分子の質量、Vは位置エネルギー、∇2 はラプラス作用素、Ψは波動関数(より正確には座標表示の波動関数)である。平たく言えば、"全エネルギーは運動エネルギーと位置エネルギーの和に等しい"ことを意味するが、以下で説明する理由により見慣れない形を取る。
特定の関連した微分演算子が与えられると、これは線形偏微分方程式である。拡散方程式でもある。
「シュレーディンガー方程式」という用語は一般式(一番上の式)と特定の非相対論的な式(3つ目の式)のどちらにも使われる。一般式はまさしく一般的で、ハミルトニアンの様々な複雑な式を代入することで、ディラック方程式から場の量子論まですべてに対して、量子力学全般で使う事ができる。特定の非相対論的な式は現実を簡略化した近似値であり、多くの場面で非常に正確であるが、一部の場面では非常に不正確である(相対論的量子力学を参照)。
シュレーディンガー方程式を適用するには、系を構成する粒子の運動・位置エネルギーから構成されるハミルトン演算子を、シュレーディンガー方程式に代入する。得られた偏微分方程式を解くことで系に関する情報を含んだ波動関数が得られる。
時間依存しないシュレーディンガー方程式

時間依存シュレーディンガー方程式は、波動関数は定常状態と呼ばれる(原子軌道、分子軌道などの「軌道」とも呼ばれる)定常波の形をとる事ができると予想している。これらの状態はとても大事で、定常状態を分類し理解する事で時間依存型シュレーディンガー方程式を解きやすくなる。非時間依存型シュレーディンガー方程式は定常状態を記述する式である(ハミルトニアンが時間に依存していないときにのみ使われる)。
非時間依存シュレーディンガー方程式 (一般式)
この方程式は、ハミルトニアンを波動関数ψに作用させた結果が、元の波動関数に比例する場合がある、と主張している。この時波動関数は定常状態と呼ばれ、比例係数Eはこの状態のエネルギーになっている。 線型代数学では、この式は固有値方程式、Eは固有値、は固有ベクトルと呼ばれる。
この非時間依存シュレーディンガー方程式を満たすに対して、
と置くと、これは時間依存型シュレーディンガー方程式を満たす事が確認できる。
前と同様に電場中(磁場はない)で動く粒子の例が有名で、以下の形になる。
非時間依存型シュレーディンガー方程式 (非相対論的単一粒子)
関連項目
シュレーディンガー方程式とその解は物理を飛躍的に進歩させた。シュレーディンガー方程式の解からは当時は予想できなかった結論が得られた。
運動、位置エネルギーとその和
式の全体的な形式はエネルギー保存の法則を使用しているため、普通でなかったり予想できないことはない。非相対論的シュレーディンガー方程式は系の全エネルギーとして解釈され、系の運動エネルギーと位置エネルギーを足しあわせたものに等しい。この側面では、古典物理学と同じである。
量子化
シュレーディンガー方程式は、系のある性質が観測されれば、結果は量子化(離散的な値だけが現れる)される事があるとしている。例として、原子中の電子のエネルギーが常にエネルギー準位のひとつを取るというエネルギーの量子化がある。これは原子分光分析で確認されている。また他の例として角運動量の量子化がある。これは初期のボーアの原子模型の時には仮定であったが、シュレーディンガー方程式から導出されるものである。
ただし量子力学ではすべての結果が量子化されるわけではない。例えば、位置、運動量、時間、そして(いくつかの状況における)エネルギーは、連続した範囲の値を取りうる。
観測と不確実性
古典力学では、粒子は常に正確な位置と正確な運動量を持つ。これらの値は粒子がニュートン力学にしたがって値を変えながら決定論的に変化する。量子力学では、粒子は正確に決まった値を持たず、観測された時に観測結果がある確率分布からランダムに決まる。シュレーディンガー方程式はその確率分布を予想するが、本質的に個々の観測の正確な結果を予想することは出来ない。 ハイゼンベルクの不確定性原理は量子力学における不確実性の有名な例である。それは、より正確に粒子の位置を確認すると運動量が曖昧になり、その逆も同様となることを主張している。 シュレーディンガー方程式は、粒子の波動関数の(決定論的な)時間発展を説明する。しかし波動関数が厳密に分かったとしても、波動関数の具体的な観測結果を決める事はできない。
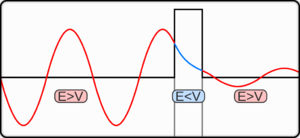
トンネル効果
古典物理学では、ボールをゆっくりと山の頂上に向けて転がすと、やがてボールは止まり、転がって戻ってくる。これはボールが山の頂上に辿り着き反対側へ行くのに必要なエネルギーを持っていないためである。しかしシュレーディンガー方程式は、ボールが頂上へたどり着くのに十分なエネルギーを持っていなくても、山の反対側へ到達する小さな可能性が存在することを予想している。これがトンネル効果と呼ばれている。これは不確定性原理に関係している。ボールが山のこちら側にいるように見えても、その位置は不確実であり、反対側で確認される可能性がある。
粒子の波動性

非相対論的なシュレーディンガー方程式は波動方程式とも呼ばれる偏微分方程式の一種である。そのためよく粒子は波として振る舞うのだと言われる。現代の多くの解釈ではこの逆に、量子状態(つまり波)が純粋な物理的な実在であり、ある適切な条件の下では粒子としての性質を示すのだとされる。
二重スリット実験は、通常は波が示す直感的には粒子と関連しない奇妙な振る舞いの例として有名である。ある場所では二つのスリットから来た波同士が打ち消し合い、別の場所では強め合うことで、複雑な干渉縞が現れる。直感的には1個の粒子のみを打ち出した時には、どちらかのスリットのみを通り両方のスリットからの寄与の重ね合わせにならないため、干渉縞は現れないように感じられる。
ところが、シュレーディンガー方程式は波動方程式であるから、一粒子のみを二重スリットに打ち出した時にも同じ干渉縞が現れる(左図)。なお、干渉縞が現れるためには実験を繰り返し何度も行う必要がある。このように干渉縞が現れるという事は個々の電子が両方のスリットを同時に通る事を示している[3][4][5]。直感と反する事ではあるが、この予言は正しく、この考えで電子回折や中性子回折をよく理解でき、科学や工学で広く使われている。
回折の他に、粒子は重ね合わせや干渉の性質を示す。 重ね合わせの性質によって、粒子は古典的には異なる2つ以上の状態を同時にとる事ができる。例えば、粒子は同時に複数のエネルギーを持つことや、異なる場所に同時にいる事ができる。二重スリットの実験の例では2つのスリットを同時にとる事ができるのである。古典的なイメージに反する事ではあるがこの重ね合わせ状態は一つの量子状態のままである。
波動関数の解釈
シュレーディンガー方程式はその系で考えられる波動関数と、それが時間によってどのように動的に変化するかを測定する方法を与える。しかし、シュレーディンガー方程式は直接的に、正しい波動関数が何であるかを語るわけではない。量子力学の解釈は、波動関数と根底にある現実、そして経験的な測定結果の間にある関係とは何か、というような問題を扱う。
大事な側面は、シュレーディンガー方程式と波動関数の崩壊の関係である。最初期のコペンハーゲン解釈では、粒子は波動関数の崩壊の間を除いてシュレーディンガー方程式に従う。波動関数の崩壊の間は全く異なった動きをする。量子デコヒーレンスの出現は、代わりのアプローチを可能にした(エヴェレットの多世界解釈のような)。それらではシュレーディンガー方程式が常に満たされ、波動関数の崩壊はシュレーディンガー方程式の成り行きとして説明される。
歴史的背景と発展
マックス・プランクの光の量子化(黒体輻射を参照)にしたがって、アルベルト・アインシュタインは、プランクの量子は光子(光の粒子)であると説明し、光子のエネルギーはその波長に比例すると提案している(これが波動と粒子の二重性の最初の現れ)。エネルギーと運動量は特殊相対性理論の波長と波数と同じ方法で関係しているから、光子の運動量pが波数kと比例関係にあることがわかる。
ルイ・ド・ブロイは、粒子が電子のようなものでも、すべての粒子に対してこの式が正しいと仮説を立てた。 彼は、物質の波が対応する物質を伝搬すると仮定すると、電子は定常波を形成する、つまり原子の核について不連続な回転周波数のみが許されることを示した[6]。 これらの量子化された軌道は不連続なエネルギー準位に対応し、デ・ブロイはボーアの原子模型がエネルギー準位を形成することを再現した。ボーアの原子模型は角運動量の量子化の仮定の上で成り立っている。
ド・ブロイにしたがうと、電子は波と波長の数が電子の軌道の円周上と合わなければいけないと説明できる。
このアプローチは本質的に、円周軌道上の一次元での電子の波に制限される。
1921年、ド・ブロイに先立ち、シカゴ大学のアーサー·C·ランが、今で言うド・ブロイの関係を導くために、相対性理論の四元運動量の完成を基にした同様の主張を使った[7] 。ド・ブロイと違って、ランは今シュレーディンガー方程式と呼ばれる微分方程式を公式化し、水素原子のエネルギーの固有値を解いた。不幸にもこの論文はフィジカル・レビューに却下されてしまった。Kamenはこの詳細を述べている[8] 。
ド・ブロイの理論が登場すると、物理学者ピーター・デバイは即座に、もし粒子が波として振る舞うなら、それらは波動方程式のいくつかを満たすべきだとコメントした。デバイの見解にインスパイアされて、シュレーディンガーは電子の適切な3次元波動方程式を見つけようとした。ウィリアム・ローワン・ハミルトンの力学と光学の類推に従い、機械系に似た光学の0波長限界の観測を符号化した(光線の軌道は、フェルマーの原理(最小作用の原理の類似物)に従って急な軌道になる)[9]。彼の論証の最新のものをいかに記述する。彼の発見した方程式は[10]
しかし同時に、アルノルト・ゾンマーフェルトは相対論補正を使ってボーアの原子模型を改良した[11][12]。シュレーディンガーは相対性理論のエネルギーと運動量の関係を使って、クーロンの法則(自然単位系)における現在クライン-ゴルドン方程式と知られるものを見つけようとした。
彼は相対論的方程式の定常波を発見したが、相対論補正はゾンマーフェルトの公式と一致しなかった。落胆して彼は計算をやめ、1925年12月、彼は人里離れた山小屋に引きこもってしまった[13] 。
山小屋でシュレーディンガーは、初期の非相対論的計算は発表に値する新しさがあると認め、将来にわたって相対論計算の問題から手を引くことを決めた。 水素原子におけるシュレーディンガー方程式の解の難しさ(後に彼は友人の数学者ヘルマン・ワイルに助けられている)にもかかわらず、シュレーディンガーは1926年に発表した論文で、波動方程式の非相対論的な式は水素の正しいスペクトルのエネルギーを算出することを示している。 方程式で、シュレーディンガーは水素原子の電子を波Ψ(x, t)として扱い、井戸型ポテンシャルVで動き、陽子で作られているとした上で、水素スペクトル系列を計算した。この計算はボーアの原子模型のエネルギー準位を正確に再現した。論文でシュレーディンガーは自分でこの方程式を以下のように説明している。
| 「 | The already ... mentioned psi-function.... is now the means for predicting probability of measurement results. In it is embodied the momentarily attained sum of theoretically based future expectation, somewhat as laid down in a catalog. | 」 |
—Erwin Schrödinger[14] | ||
この1926年の論文はアインシュタインに熱狂的に支持された。アインシュタインは物質の波を自然の直感的な表し方として見ており、ハイゼンベルクの行列力学をあまりに形式的だと非難していた[15] 。
シュレーディンガー方程式は波動関数ψの動きの詳細を述べるが、自然について何も語らない。シュレーディンガーは4番目の論文で、これを密度の変化として理解しようとしたが、失敗した[16]。1926年、シュレーディンガーの4番目で最後の論文が発表された数日後、マックス・ボルンは波動関数ψを確率振幅(二乗した絶対値が確率密度に等しい)として解釈することに成功した[17]。しかしシュレーディンガーは常に統計学的、確率的なアプローチと、それに関連した波動関数の崩壊を反対しており(アインシュタインのように、量子力学は決定論の統計学的近似であると信じていた)、ついにコペンハーゲン解釈と和解することはなかった[18]。
粒子の波動関数
シュレーディンガー方程式はド・ブロイの仮説である粒子を説明する波動関数により発展され[19] 、以下の方法で構築される[20]。シュレーディンガー方程式の正しい数学的導出も記す[21]。
仮定
エネルギー保存則:粒子の全エネルギーEは、運動エネルギーTと位置エネルギーVの和である。この和は古典力学では、ハミルトニアンHを表すためにもよく使われる。
明示的に、一次元の粒子を、位置x、質量m、運動量p、位置によって変化する位置エネルギーV、そして時間tとすると
三次元では、位置ベクトルrと運動量ベクトルpが使われる。
この形式論は粒子の任意の定数にまで拡大できる。系の全エネルギーは粒子の全運動エネルギーと、全位置エネルギーを足しあわせたものであり、またハミルトニアンでもある。しかし、粒子間には相互作用(多体問題)がある可能性があるため、位置エネルギーVは粒子の形状空間の変化と、あるいは時間によって変化する。一般的には位置エネルギーは、それぞれの粒子の異なる位置エネルギーの合計ではなく、粒子のすべての空間位置の関数である。明示的に、
ド・ブロイの関係:アインシュタインの光電効果仮説(1905年)によれば、光子のエネルギーEは、光の対応する量子波束の周波数ν(もしくは角周波数ω = 2πν)に比例する。
同様に、ド・ブロイの仮説(1924年)によれば、どの粒子も波と関連付けることが出来、粒子の運動量pは、その一次元での波の波長λに関係している。
三次元では
kは、波ベクトル(波長はkの大きさに関係する)である。
線形性:前の仮定は、自由粒子に対応した平面波の方程式を導くことのみを可能にする。一般的には、物理的状況は単に平面波で説明されるわけではない。そのため一般的に重ねあわせが求められる(いずれの波も正弦の平面波の重ね合わせで作られる)。そのため方程式が線形性であれば、平面波の線形結合もまた解くことができる。それゆえ必要で独自の必要条件は、シュレーディンガー方程式が線型微分方程式であることである。
まとめると、これらの特質は、粒子のエネルギー(粒子の系における運動エネルギーと位置エネルギーは、系の状態のいくつかの関数の点から、粒子に持たせる。)と波動関数(Ψと定義される)を基にして方程式を作ることを示唆している。 波動関数は系での制限のもと、粒子の量子状態を要約する(どこかの時点、どこかの形状空間に粒子がある確率)。波動関数に対してこれを解くことは、粒子が特定の位置、それぞれの影響を受けてどのように動くかを予測するために使われる。
方程式の解
シュレーディンガー方程式は数学的に波動方程式であるから、その解は波のような動きを説明する関数である。 普通、物理学での波動方程式は他の物理的法則から導くことができる(バネやその他物質の自然振動の波動方程式はニュートンの法則から求められる)。アナログの波動関数は物質の変位であり、波動関数が電場と磁場である場合、マクスウェルの方程式の電磁波である。 それとは逆に、シュレーディンガー方程式の基礎は粒子のエネルギーと、量子力学の仮定(波動関数は型の説明である)である。シュレーディンガー方程式はそれゆえ、ファインマンが言うように、それ自身の新しい概念である。
| 「 | Where did we get that (equation) from? Nowhere. It is not possible to derive it from anything you know. It came out of the mind of Schrödinger. | 」 |
—Richard Feynman[22] | ||
例えば、電子波の粒子のような動きは、以下に記すように、適切な状況下ではシュレーディンガー方程式に従う。この行動はしばしば粒子と波動の二重性と呼ばれる。
プランク-アインシュタイン、ド・ブロイの関係
は、運動量と空間、時間とエネルギーの間の深い関係を明らかにする。これは自然単位系を使い、ħ = 1と設定して方程式を以下の恒等式にすると、より明白となる。
エネルギーと角周波数は、時間の逆数として同じ次元を持ち、運動量と波数は逆の長さの次元を持つ。実際にそれらは交互に使われる。量子の重ねあわせを防ぎ、量子に関連した次元の数を減らす。知られるように、SI単位はこの条項で使われる。
1925年の終わり、シュレーディンガーの見識は、平面波の位相は以下の関係を使って複素数の力率として表した。
そして空間に対する一次偏微分を
そして時間に対して
導関数を示す
もう一つの量子力学の仮定は、すべての観測は波動関数に作用する線形演算子に表され、演算子の固有値は観測可能な値である。前の導関数は、時間微分に対応するエネルギー演算子と
空間微分(ナブラ)に対応する運動量演算子を導く。
サーカムフレックス(帽子)は、観測量が演算子であると定義する。それらは、乗数的因子の位置エネルギーを除いて微分演算子である。面白い点は、エネルギーは時間に関して対称性で、運動量は空間に関して対称性であり、そしてそれらはエネルギーと運動量が保存則である理由である。ネーターの定理を参照。
エネルギー方程式にΨを掛け、エネルギー・運動量演算子を置換する。
すぐにシュレーディンガーに彼の方程式を導く。
これらの方程式は、粒子と波の二重性に以下のような評価を可能にする。運動エネルギーTは運動量pの平方に関係する。粒子の運動量が増えれば、運動エネルギーはより早く増加する。しかし波数kが増加するため、波長が減少する。
そして運動エネルギーは二次空間微分に比例するから、波の曲率の強さにも比例する。
曲率が増える毎に、波の振幅は正負を互い違いにより速く動き、波長を短くする。そのため運動量と波長の逆関係は、粒子の持つエネルギーと一致し、そのため粒子のエネルギーは波との結合を持ち、全てが同じ数学式にある[19]。
方程式の解
方程式の一般的な解は、以下のように簡単に見ることができる。平面波は方程式の構成に使われるため、確かに平面波は解である。そのため平面波の線形結合の直線性もまた解である。不連続のkでは、合計は平面波の重ねあわせである。
連続のkでは合計は積分で、運動量空間波動関数のフーリエ変換である[23]。
d3k = dkxdkydkzはK空間での微分体積要素であり、積分は空間から引き継がれる。運動量波動関数Φ(k) は、位置と運動量空間がそれぞれのフーリエ変換であるから、被積分関数から生じる。 それらはシュレーディンガー方程式を満たすから(与えられた状況に対するシュレーディンガー方程式の解は平面波のみならず、系や関連した境界条件に制限されるいかなる波動関数もある)、シュレーディンガー方程式はどの非相対論的な状況に対しても正しいと結論付けられる。
要約すると、シュレーディンガー方程式は波と粒子の二重性の微分方程式であり、粒子は方程式を満たす波動関数と関係するから、波のようにも振る舞う。
波と粒子の動き
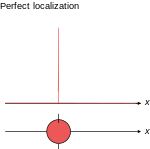
シュレーディンガーは、k付近での波ベクトルと位置rの近くでの波束解が、rでの幅を増やさない程度にk(と速度)の幅に対して短い時間で古典力学によって定められた曲線を描く。kの幅が与えられると、速度の広がりはプランク定数に比例するから、プランク定数をゼロに近似したとき、古典力学での方程式は量子力学から戻されると言われる[24]。その極限がどのように取られるか、またどんな状況でかという点で最新の注意が払われる必要がある。
短波長限界はプランク定数をゼロに近似した値と等しい。なぜならプランク定数は、粒子の定位置に局所化する波束を増やす限界値であるためである(右図を参照)。ハイゼンベルクの不確定性原理を位置と運動量に対して使うと、位置と運動量の不確定性の産物は、ħ → 0に従ってゼロとなる。
σはxと、(y軸とz軸でも同様に)位置と運動量がこの極限で任意の精度で知られることを表すpxの観測不確実性の二乗平均平方根である。
シュレーディンガー方程式の一般式
はハミルトン-ヤコビ方程式: と密接に関連している。
Sは運動、Hはハミルトニアン関数(演算子ではない)。一般化座標系qi for i = 1,2,3(ハミルトンヤコビ方程式で使われる)は、r = (q1, q2, q3) = (x, y, z)としてデカルト座標系に位置を決定される[24]。
代入式
ρはシュレーディンガー方程式に対する確率振幅で、結果として生じる方程式で極限 ħ → 0を取り、ハミルトン-ヤコビ方程式を算出する。
関わりあいは、
- 粒子の動き(シュレーディンガー方程式の(短波長)波束解で説明される)は、動きのハミルトン-ヤコビ方程式により説明される。
- シュレーディンガー方程式は波動関数を含み、そのため波束解は(量子)粒子の位置が、波面にあいまいに広がることを示している。それどころか、ハミルトン-ヤコビ方程式は、定位置定運動量の(古典的)粒子に適用され、その代わり(軌道上の)位置や運動量は決定論的で、同時に知られる。
特殊な場合
以下は、異なる状況(時間依存や非依存、一次元と三次元、一つまたはN個の粒子)に対してシュレーディンガー方程式のいくつかの形式である。実際的に、系を構成する粒子は理論で使われる数のラベルを持ってはいない。数学の言語は我々に、粒子の位置に一通りかその他のラベル付けを迫り、さもなければ粒子の変数を表す記号に対して混乱が生じてしまう[21]。
時間非依存

ハミルトニアンが時間の陽関数であるなら、方程式は次元と時間の部分に分離できる。すなわち。そのためエネルギー演算子はエネルギー固有値Eに置き換えられることができる。抽象的な形では、これはハミルトニアンに対する固有方程式である[25]。
時間非依存型方程式の解は、エネルギーEのエネルギー固有状態と呼ばれる[23]。
状態の時間依存を見つけるには、初期状態ψ(r)と共に時間依存方程式について考える。t = 0 での時間微分は、どこでもその値に比例する。
そのため、最初の全体の関数は大きさを変え、時間微分がそれ自身に対して比例であるという特性を維持する。そのためすべての時間tに対して
Ψを代わりに使い
ψ(r)は消し、そのためでのこの方程式の解は、初期状態での時間依存方程式の解を意味している[10]。
この場合は(異なるエネルギーの確率分布の代わりの)一定のエネルギーと状態である、時間依存方程式の定常波解を説明する。物理学では、これらの定常波は基底状態やエネルギー固有状態と呼ばれる。化学では原子軌道や分子軌道と呼ばれる。エネルギー固有状態の重ね合わせは、エネルギー準位間の相対位相に従ってそれらの特性を変える。
この方程式から得られるエネルギー固有値は、値の離散スペクトルを形成する。そのため、計算上はエネルギーは量子化されているはずである。より明白に言えば、エネルギー固有値は基礎(いかなる波動関数も離散エネルギー状態の合計、または連続エネルギー状態の積分、または計測量の積分により表現される)を形成する。これは数学のスペクトル定理であり、有限状態空間でのエミルート行列の固有ベクトルの完全性と呼ばれるものである。
原子や分子の場合、原子の離散スペクトル線が、エネルギーが原子で物理的に量子化されているという証拠であるというスペクトル定理に現れる。特に、原子には、電子の原子または分子軌道(定常状態、波動関数)に関連したエネルギー準位がある。観測されたスペクトル線は一定の光の波長であり、上に述べたプランク-アインシュタインの関係とデブロイの関係での、一定のエネルギーと関連している。しかし、これはエネルギー準位の絶対値ではなく、観測された周波数を作るそれらの違いは、原子が放出/吸収した光の光子間の電子遷移が原因である。
式のまとめ
下にまとめたものはハミルトニアンが取る様々な形であり、シュレーディンガー方程式と、波動関数の解の形式に関連している。一次元の場合では、一つの粒子に対し、偏微分を通常の微分で解くことを注意。
| 1粒子 | N 粒子 | |
| 一次元 |
粒子 nの位置はxn。 | |
|
さらに制約がある。解は無限に大きくなり、そのため有限なL2ノルム(束縛状態であるなら)か、ゆるやかに発散するノルム(連続体の一部なら)を持つ必要がある。 [26]
|
相互作用しない粒子では
| |
| 三次元 |
粒子の位置はr = (x, y, z)。 |
粒子 nの位置はr n = (xn, yn, zn)で、対応した位置座標を使った粒子 nのラプラシアンは |
|
相互作用しない粒子では
|
以下は正確な解が知られている例である。詳細は記事を参照。
一次元の例
自由粒子
電位がなく、V = 0 であるとき、粒子は自由で、方程式が解釈される[27]
E > 0(Cnは任意定数)での振動の解を持つ。
E < 0で指数解を持つ。
指数的に増大する解は無限ノルムを持ち、物理学ではない。それらは周期的、または固定した束縛状態で有限値を取らない。
定電位

定電位、V = V0のとき、古典力学で許されるかどうかのエネルギーに従って、解はE > V0 で振動、E < V0で指数である。振動解は古典力学で許されるエネルギーを持ち、実際の古典的な動きに対応する。一方指数解は許されないエネルギーを持ち、量子トンネルのため、粒子の少量が古典的に許されない位置へ滲んでいくことを説明する。電位V0が無限で大きくなるなら、動きは有限域に限定され、これは量子力学で全ての解がべき乗になることを意味する。指数が減少する状態はエネルギー準位を離散集合へ制限し、allowd energyと呼ばれる[23]。
調波発振器

この解に対するシュレーディンガー方程式は
これは解くために注目すべき量子系である。解は正確で(だがエルミート多項式のために複雑)、振動準位[28]や、原子または格子のイオン[29]、均衡点に近いほかの電位を含む、他の系の豊富な種類を近似するか、説明することができるから。これは量子力学における摂動でもある。
解の仲間がある。位置を基準にそれらは
n = 0,1,2...と、関数Hnはエミルート多項式である。
三次元の例
水素原子
シュレーディンガー方程式の形式は、水素原子に応用ができる[19][30]。
eは電気素量で、rは電子の位置(r = |r|は位置の大きさ)、電位の項はクーロンの法則のためで、ε0は電気的定数(自由空間の誘電率)で
は、質量mpの水素原子核と質量meの電子の二体換算質量である。陽子と電子は振動的に変化するから、電位の項に負符号が現れる。電子と陽子が質量の同じ中心についてそれぞれ軌道を回り、解決のために二体問題を構成するから、電子質量の場所の換算質量が使われる。電子の動きは原理的な重大性があり、そのため同等の一体問題は換算質量を使った電子の動きである。
水素に対する波動関数は電子の座標の関数で、実際にはそれぞれの座標の関数に分離できる[31]。よくこれは球面座標系でなされる。
Rは放射関数で、は深度ℓと状態mの球面調和関数である。これはシュレーディンガー方程式が正確に解かれる原子のみ。多電子原子は近似方法を必要とする。解の仲間は[32]
ここで
ラゲールの陪多項式は著者によって異なるように定義されるため、その記事や水素原子の記事を見よ。
ニ電子原子またはイオン
中性のヘリウム原子(He, Z = 2)や、陽イオンの水素イオン(H–, Z = 1)、陰イオンのリチウムイオン(Li+, Z = 3)のような、いかなる二電子系に対する方程式は[20]、
r1はひとつの電子の位置(r1 = |r1| はその大きさ)で、r2は他の電子の位置(r2 = |r2| はその大きさ)である。r12 = |r12|はそれらの間の距離の大きさであり、以下で与えられる。
μは再び質量Mの原子核に対応した電子の二体換算質量であり、ここでは
ラプラシアンの交差項
は、mass polarization termとして知られ、原子核の運動が原因で現れる。波動関数は二つの電子の位置の関数である。
この方程式に対する閉形式解はない。
時間依存
これは量子状態に対する運動の方程式である。最も一般的な形式は、以下のように書かれる[25]。
形式のまとめ
再び、シュレーディンガー方程式や解の形式に関連した、ハミルトニアンが取る様々な形式のまとめをいかに記す。
| 1粒子 | N粒子 | |
| 一次元 |
粒子nの位置はxnである。 | |
| 三次元 | ||
|
この最後の方程式は、高次元でのものである[33]。そのため解は視覚化が容易でない。 | ||
解き方
|
一般的な技術
|
|
脚注
- ^ J.J. Sakurai『現代の量子力学』 上、桜井明夫訳、吉岡書店〈物理学叢書56〉、1989年2月。ISBN 978-4-8427-0222-3。
- ^ Physics for Scientists and Engineers - with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman
- ^ O Donati G F Missiroli G Pozzi May 1973 An Experiment on Electron Interference American Journal of Physics 41 639–644
- ^ Brian Greene, The Elegant Universe, p. 110
- ^ Feynman Lectures on Physics (Vol. 3), R. Feynman, R.B. Leighton, M. Sands, Addison-Wesley, 1965, ISBN 0-201-02118-8
- ^ de Broglie, L. (1925). “Recherches sur la théorie des quanta”. Annales de Physique 10 (3): 22–128. Translated version.
- ^ Weissman, M.B.; V. V. Iliev and I. Gutman (2008). “A pioneer remembered: biographical notes about Arthur Constant Lunn”. Communications in Mathematical and in Computer Chemistry 59 (3): 687–708.
- ^ Kamen, Martin D. (1985). Radiant Science, Dark Politics. Berkeley and Los Angeles, CA: University of California Press. pp. 29–32. ISBN 0-520-04929-2
- ^ Schrodinger, E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN 3-7001-0573-8 See introduction to first 1926 paper.
- ^ a b Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, (Verlagsgesellschaft) 3-527-26954-1, (VHC Inc.) ISBN 0-89573-752-3
- ^ Sommerfeld, A. (1919). Atombau und Spektrallinien. Braunschweig: Friedrich Vieweg und Sohn. ISBN 3-87144-484-7
- ^ For an English source, see Haar, T.. The Old Quantum Theory.
- ^ Rhodes, R. (1986). Making of the Atomic Bomb. Touchstone. ISBN 0-671-44133-7
- ^ Erwin Schrödinger, "The Present situation in Quantum Mechanics," p. 9 of 22. The English version was translated by John D. Trimmer. The translation first appeared first in Proceedings of the American Philosophical Society, 124, 323-38. It later appeared as Section I.11 of Part I of Quantum Theory and Measurement by J.A. Wheeler and W.H. Zurek, eds., Princeton University Press, New Jersey 1983).
- ^ Einstein, A.; et. al.. Letters on Wave Mechanics: Schrodinger-Planck-Einstein-Lorentz.
- ^ Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 219. ISBN 0-521-43767-9
- ^ Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 220. ISBN 0-521-43767-9
- ^ It is clear that even in his last year of life, as shown in a letter to Max Born, that Schrödinger never accepted the Copenhagen interpretation (cf. p. 220). Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 479. ISBN 0-521-43767-9
- ^ a b c d Quanta: A handbook of concepts, P.W. Atkins, Oxford University Press, 1974, ISBN 0-19-855493-1
- ^ a b Physics of Atoms and Molecules, B.H. Bransden, C.J.Joachain, Longman, 1983, ISBN 0-582-44401-2
- ^ a b Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd Edition), R. Resnick, R. Eisberg, John Wiley & Sons, 1985, ISBN 978-0-471-87373-0
- ^ The New Quantum Universe, T.Hey, P.Walters, Cambridge University Press, 2009, ISBN 978-0-521-56457-1
- ^ a b c Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, ISBN(10) 0 07 145546 9
- ^ a b Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
- ^ a b Shankar, R. (1994). Principles of Quantum Mechanics. Kluwer Academic/Plenum Publishers. pp. 143ff. ISBN 978-0-306-44790-7
- ^ Feynman, R.P.; Leighton, R.B.; Sand, M. (1964). “Operators”. The Feynman Lectures on Physics. 3. Addison-Wesley. pp. 20–7. ISBN 0-201-02115-3
- ^ Shankar, R. (1994). Principles of Quantum Mechanics. Kluwer Academic/Plenum Publishers. pp. 151ff. ISBN 978-0-306-44790-7
- ^ Physical chemistry, P.W. Atkins, Oxford University Press, 1978, ISBN 0-19-855148-7
- ^ Solid State Physics (2nd Edition), J.R. Hook, H.E. Hall, Manchester Physics Series, John Wiley & Sons, 2010, ISBN 978-0-471-92804-1
- ^ 引用エラー: 無効な
<ref>タグです。「Quantum Chemistry 1977」という名前の注釈に対するテキストが指定されていません - ^ Physics for Scientists and Engineers - with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7
- ^ David Griffiths (2008). Introduction to elementary particles. Wiley-VCH. pp. 162–. ISBN 978-3-527-40601-2 27 June 2011閲覧。
- ^ Shankar, R. (1994). Principles of Quantum Mechanics. Kluwer Academic/Plenum Publishers. p. 141. ISBN 978-0-306-44790-7







![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4894f9a205c471cb012351a1fccdd01285b6f11c)


![{\displaystyle |\Psi ({\boldsymbol {r}},t)\rangle =\exp \left[-{\frac {i}{\hbar }}Et\right]|\Psi ({\boldsymbol {r}})\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/efd60f97b809450e55216039eafcba14f9008dbb)




































































![{\displaystyle \psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aaf51710a4718d8bd8bd8ddb947836b6bd0f30e)



![{\displaystyle E\psi =-\hbar ^{2}\left[{\frac {1}{2\mu }}\left(\nabla _{1}^{2}+\nabla _{2}^{2}\right)+{\frac {1}{M}}\nabla _{1}\cdot \nabla _{2}\right]\psi +{\frac {e^{2}}{4\pi \epsilon _{0}}}\left[{\frac {1}{r_{12}}}-Z\left({\frac {1}{r_{1}}}+{\frac {1}{r_{2}}}\right)\right]\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c8d25001a4a294e7d0e0f2daa1fe0edcf56f34f)
















