プリム法

プリム法とは、グラフ理論で重み付き連結グラフの最小全域木を求める最適化問題のアルゴリズムである。全域木（対象となるグラフの全頂点を含む辺の部分集合で構成される木）のうち、その辺群の重みの総和が最小となる木を求めるものである。このアルゴリズムは1930年に数学者 Vojtěch Jarník が発見し、1957年に計算機科学者ロバート・C・プリムが独自に発見、さらに1959年にはエドガー・ダイクストラが再発見しダイクストラ法の論文に記載している。そのため、DJP法、Jarník法、Prim-Jarník法などとも呼ばれることがある。アルゴリズムの発想や計算量は同時期に発表されたダイクストラ法に類似している。

アルゴリズムの解説

このアルゴリズムでは1つの辺から始めて、全頂点を覆うようになるまで連続的に木の大きさを拡大していく。

入力: 重み付きグラフ（頂点集合 V、辺集合 E）
出力: V_new と E_new が最小全域木を表している。

V_new = {x}、ここで x は V の元であり、任意のノード（出発点）
E_new = {}

while (V_new ≠ V)
    V_new に含まれる頂点 u と 含まれない頂点 v を結ぶ重みが最小の辺 (u, v) を E から選択（同じ重みの辺が複数あるときは、どちらを選んでも良い）
    v を V_new に加える
    (u, v) を E_new に加える

計算量

V は頂点の数、E は辺の数。「重みが最小の辺」をどのように探索するかで計算量が変わる。

使用するデータ構造	計算量
単純な集合探索と隣接行列	$O(V^{2})$
優先度付きキュー（二分ヒープ）と隣接リスト	$O((V+E)\log V)=O(E\log V)$
優先度付きキュー（フィボナッチヒープ）と隣接リスト	$O(E+V\log V)$

グラフを隣接行列で表した単純な実装で、重みの配列を探索して重みが最小の辺を求める場合、 $O(V^{2})$ の時間がかかる。単純な二分ヒープと隣接リストを使うと、 $O((V+E)\log V)$ の時間がかかる。より洗練されたフィボナッチヒープを使うと、E が $\Omega (V\log V)$ の程度まで稠密であれば、時間は $O(E+V\log V)$ とかなり改善される。

例

イメージ	説明
	グラフの初期状態。辺のそばにある数は重み（距離）を表す。
	頂点 D を出発点として選ぶ（任意）。頂点 D と1つの辺で接続している頂点は A、B、E、F である。A が D に最も近いので、辺 AD と共に次の頂点として選択する。
	次に D または A に最も近い頂点を選ぶ。B は D からは9で A からは7離れている。Eは15、Fは6である。従って F が最も近いので、頂点 F と辺 DF を選ぶ。
	同様に、A から7だけ離れている B を選ぶ。
	残る頂点は C、E、G である。C は B から8離れており、E は B から7離れており、G は F から11離れている。E が最も近いので、頂点 E と辺 EB を選ぶ。
	残る頂点は C と G だけである。C は E から5離れており、G は E から9離れている。従って C を選び、同時に辺 EC を選ぶ。
	頂点 G だけが残っている。F からは11離れていて、E からは9離れている。E の方が近いので、辺 EG を選ぶ。
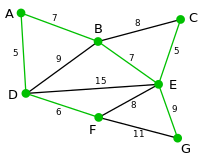
	以上で全頂点の選択が終了し、最小全域木を緑色で示している。この場合の重みの総和は39である。

擬似コード

Min-heap

初期化

入力: グラフ graph、辺の重みを返す関数 weight-function、初期頂点 initial vertex
全頂点をまだ見ていない状態に初期化し、initial vertex を木に追加し、最小グラフから最小距離を除去することを考慮して全ての頂点を min-heap Q に置く。

for each vertex in graph
   set min_distance of vertex to ∞
   set parent of vertex to null
   set minimum_adjacency_list of vertex to empty list
   set is_in_Q of vertex to true
set distance of initial vertex to zero
add to minimum-heap Q all vertices in graph.

アルゴリズム

上の初期化アルゴリズムで、次の状態になっている。

nearest vertex とは Q[0] にあり、これが最新の追加である。
fringe とは Q 上の v であり、最も近い頂点を除去した後で v の距離が ∞ より小さいもの。
not seen とは Q 上の v であり、最も近い頂点を除去した後で v の距離が ∞ であるもの。

このwhileループは、remove minimum がヌルを返すと終了する。隣接リストは有向グラフを返せるように設定する。

時間計算量: ループについては V、remove 関数については log(V)

while latest_addition = remove minimum in Q
    set is_in_Q of latest_addition to false
    add latest_addition to (minimum_adjacency_list of (parent of latest_addition))
    add (parent of latest_addition) to (minimum_adjacency_list of latest_addition)

時間計算量: E/V、平均頂点数

    for each adjacent of latest_addition
    if (is_in_Q of adjacent) and (weight-function(latest_addition, adjacent) < min_distance of adjacent)
        set parent of adjacent to latest_addition
        set min_distance of adjacent to weight-function(latest_addition, adjacent)

時間計算量: log(V)、ヒープの深さ

        update adjacent in Q, order by min_distance

正しさの証明

P を重み付き連結グラフとする。プリム法の繰り返しでは、毎回ある部分グラフからその外部へと接続している辺を探し出す。P は連結グラフなので、全ての頂点に常に道が存在する。プリム法の出力 Y に追加される辺と頂点はつねに接合しているため、Y は木である。Y₁ が P の最小全域木であるとする。Y₁=Y なら、Y は最小全域木である。そうでない場合、Y にあって Y₁ にない辺のうち、Y の構築時に最初に追加された辺を e とし、e が追加される以前に追加された辺に接合している頂点の集合を V とする。e の端点の一方は V にあり、もう一方はそうではない。Y₁ は P の全域木なので、Y₁ にはその2つの端点をつなぐ道がある。その道をたどると、V 内の頂点から V 外の頂点への辺 f に必ず遭遇する。さて、Y に e を追加した時の繰り返しにおいて、e よりも f の方が重みが小さければ f が追加されていただろう。しかし f は追加されなかったので、次の結論が得られる。

w(f) ≥ w(e)

Y₁ から f を除いて e を追加したグラフを Y₂ とする。Y₂ が連結グラフであり、Y₁ と同数の辺を持ち、辺の重みの総和が Y₁ より小さいことは容易に示すことができる。従って、これも P の最小全域木であり、e を含み、それ以前に V の構築の際に追加された全ての辺を含んでいる。以上を繰り返し適用していくと、Y と全く同じ P の最小全域木を得られる。以上から、Y は最小全域木であることがわかる。

最小全域木問題の他のアルゴリズムとしてクラスカル法やブルーフカ法がある。

参考文献

V. Jarník: O jistém problému minimálním [About a certain minimal problem], Práce Moravské Přírodovědecké Společnosti, 6, 1930, pp. 57-63. (in Czech)
R. C. Prim: Shortest connection networks and some generalisations. In: Bell System Technical Journal, 36 (1957), pp. 1389–1401
Dijkstra, E.W. (1959). A note on two problems in connexion with graphs. In Numerische Mathematik, 1 (1959), S. 269 ～ 271.
D. Cherition and R. E. Tarjan: Finding minimum spanning trees. In: SIAM Journal of Computing, 5 (Dec. 1976), pp. 724–741
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 23.2: The algorithms of Kruskal and Prim, pp.567–574.

外部リンク