利用者:Yushu-kasai/sandbox/対数

このページはYushu-kasaiの利用者サンドボックスです。編集を試したり下書きを置いておいたりするための場所であり、百科事典の記事ではありません。Yushu-kasai以外の利用者は編集しないでください。
ただし、現在Yushu-kasaiがこの下書きを記事名前空間に投稿する予定はありません。会話ページにてお問い合わせ頂ければ、この下書きを委譲出来る場合があります。

数学における対数（たいすう、英：logarithm）とは、数 $x$ を $b p$ と表した時の冪指数 $p$ であり、「底を $b$ とする数 $x$ の対数（英：the logarithm of a number $x$ to the base $b$ ）」と一般に表記される。例えば、 $1000 = 10 3$ であるが、この時、底を $10$ とする $1000$ の対数は $3$ となる。底を $b$ とする $x$ の対数は、通常 $log b (x)$ または括弧抜きで $log b x$ 、混同の可能性が無い時やランダウ記法のような底が意味を持たない時は、底も省略して $log x$ と表記される。この時、 $x$ に当たる数は、真数（しんすう、英: antilogarithm）と呼ばれる。また、数 $x$ に対応する対数を与える関数を考えることができ、そのような関数を対数関数と呼ぶ。対数関数は指数関数の逆関数である。

$10$ を底とする対数は、常用対数と呼ばれ、科学や工学の分野で一般的に使用される。自然対数とは、ネイピア数 $e \approx 2.718$ を底に持つ対数で、非常に単純な導関数となるため、数学や物理学の分野で広く使用されている。二進対数は、底を $2$ とする対数で、計算機科学の分野で頻繁に使用される。

対数は、計算を簡略化する手段として、1614年にジョン・ネイピアによって導入されたのが始まりである。その後、精度の高い計算をより簡単に行うために、航海士、科学者、工学者、測量士などに対して急速に普及していった。以下の公式の通り、ある因数同士の積の対数は、その因数の対数の和に等しいため、対数表を用いれば、複数桁に及ぶ繁雑な計算を、簡単な足し算に置き換えることができる。

\log _{b}(xy)=\log _{b}x+\log _{b}y,

ただし、 $b, x, y$ は全て正で、また $b \neq 1$ でなければならない。計算尺は、対数の原理を用いた計算用具であり、対数表を用いずに即座に計算結果を求めることができる一方、精度は低くなる。

こんにちの対数の概念は、18世紀の数学者レオンハルト・オイラーによるものである。オイラーは対数の概念を指数関数の概念と関連付けた他、ネイピア数 $e$ を定義した数学者でもある。

対数目盛を使用することで、広範囲にわたる正の値を、より小さな範囲で表すことができる。例えば、デシベル（dB）は、電磁波の減衰量、音圧レベル、振動加速度レベルの3つの物理量を、基準となる量に対する比の対数で表す単位である。またpHは、化学において水溶液の酸性度を対数的に表現する単位である。他にも対数は、科学における公式、計算複雑度やフラクタル図形の測定などに用いられる。更には、音程の振動数比を表記したり、素数の数を数えたり、階乗値の近似値を求めたりする公式に現れたり、精神物理学のモデル生成や法廷会計学における情報処理などに役立ったりする。

対数関数の概念は、他の数学的概念にも拡張できる。ただし、一般的に、そのような対数関数は多価関数になる傾向が高い。例えば、複素対数関数は複素指数関数の逆関数たる多価関数である。また、離散対数は、有限群における指数関数の逆関数たる多価関数であり、これは公開鍵暗号のシステムの構築に応用されている。

導出[編集]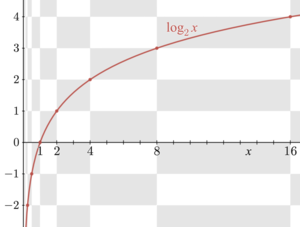

加法、乗法、冪乗は最も基本的な数学的算法のうちの3つである。加法の逆は減法で、乗法の逆は除法であるのと同様に、対数は冪乗算の逆演算である。冪乗とは、底数 $b$ を冪指数 $y$ で累乗して、計算結果 $x$ を得ることである。

b^{y}=x.

例えば、

2

の

3

乗は

8

である。

2^{3}=8.

b

を底とする対数演算は、その逆の操作にあたり、

x

を入力すると、

y

が出力される。すなわち、

b

が正の実数でありかつ

1

でない時、

y=\log _{b}x

と

x=b^{y}

とは同値である。

以下の公式の存在は、対数を利用するのに対する歴史的な動機を与えた：

\log _{b}(xy)=\log _{b}x+\log _{b}y

この公式により、コンピュータが発明される以前は、対数を計算するための乗算、除算などの煩雑な計算を、対数表の参照と簡単な加算、減算の計算とに簡略化することができた。

定義[編集]

$1$ でない正の実数 $b$ が与えられた時、底を $b$ とする正の実数 $x$ の対数は、計算結果 $x$ を得るのに必要な $b$ を累乗する指数となる。換言すれば、 $b$ を底とする $x$ の対数は、 $b^{y}=x$ を満たすような一意の実数 $y$ となる^[1]。「底を $b$ とする $x$ の対数」は「 $log b x$ 」と表記される。

同等のより簡潔な定義は、関数 $log b$ を写像 $x\mapsto b^{x}$ の逆写像と定義するものである。

例[編集]

$log 2 16 = 4$ , なぜなら $24 = 2 \times 2 \times 2 \times 2 = 16$ .
対数は負の数にもなり得る： ${\textstyle \log _{2}\!{\frac {1}{2}}=-1}$ , なぜなら ${\textstyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}}$ .
$log 10150$ は $2$ と $3$ の間の約 $2.176$ の値をとる。なぜなら、真数 $150$ は $102 = 100$ と $103 = 1000$ の間にある故。
任意の底 $b$ について、 $log b b = 1$ および $log b 1 = 0$ が成り立つ、なぜならそれぞれ $b 1 = b$ かつ $b 0 = 1$ .

対数法則[編集]

詳細は「対数法則の一覧（英語版）」を参照

対数には以下に示すような法則・公式が成り立ち、これらを対数法則または対数恒等式（英：Logarithmic identities）などと言う^[2]^{[注 1]}。

積・商・冪乗・冪根の対数[編集]

因数同士の積の対数は、それぞれの因数の対数の和となる。2数の比の対数は、それぞれの数の対数の差となる。また、ある数の $p$ 乗の数の対数は、その数の対数の $p$ 倍となる。さらには、ある数の正の $p$ 乗根の数の対数は、その数の対数を $p$ で割った値となる。2数 $x, y$ に関する次の値の対数は、以下の表の通りになる。これらの公式は、対数の定義式 $x=b^{\,\log _{b}x}$ または $y=b^{\,\log _{b}y}$ のいずれかより導かれる。

	公式	計算例
積	${\textstyle \log _{b}(xy)=\log _{b}x+\log _{b}y}$	${\textstyle \log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5}$
商	${\textstyle \log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y}$	${\textstyle \log _{2}16=\log _{2}\!{\frac {64}{4}}=\log _{2}64-\log _{2}4=6-2=4}$
冪乗	${\textstyle \log _{b}\left(x^{p}\right)=p\log _{b}x}$	${\textstyle \log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6}$
冪根	${\textstyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}$	${\textstyle \log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

底の変換[編集]

対数 $log b x$ は、以下に示す底の変換公式を用いて、任意の実数 $k$ を底とする $b$ と $x$ の対数に変形することができる^{[注 2]}。

\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.

特に、

x \neq 1

かつ

k = x

の時、

\log _{b}x={1 \over \log _{x}b}

である。

一般的な関数電卓は、常用対数または自然対数を用いて対数計算の処理を行う^[3]。底の変換公式を用いると、任意の底 $b$ の対数について、以下の式のように2つの対数のうちいずれかの既知の値を使って、その値を算出できる。

\log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.

また、未知数 $b$ を底とする $x$ の対数 $y$ が与えられた時、底は

b=x^{\frac {1}{y}},

の式で求まる。これは、対数の定義式

x=b^{\,\log _{b}x}=b^{y}

を

{\tfrac {1}{y}}

乗することにより導かれる。

特殊な底[編集]

対数は、 $1$ でない全ての正の実数を底にとることができるが、底として特に一般的なのは、 $2$ 、 $e$ 、 $10$ の3つである。ネイピア数 $e$ を底とする自然対数は解析学で広く使われている一方、 $10$ を底とする常用対数は十進法の筆算に容易に使うことができる^[4]。

\log _{10}(10x)=\log _{10}10+\log _{10}x=1+\log _{10}x.\

例えば、対数

log 10 (x)

の値を求めることにより、正の整数

x

の桁数を求めることができる。具体的には、

log 10 (x)

の値より大きい最小の整数がその桁数となる。

log 10 (1430)

の値は約3.15で、これより大きい最小の整数は4であり、これは整数1430の桁数である。

自然対数と、2を底とする二進対数とは、情報量を表す単位であるナットとビットとをそれぞれ扱うのに用いられる。また、二進対数は二進法が用いられる計算機科学でも使用される。音楽理論においては、音程差を表す単位として、二進対数の対数単位であるセントが用いられている他、撮影におけるEV値、輝度、シャッター速度、開口時間、フィルム速度などを測定するのにも応用されている^[5]。

一般的な対数の底と、対数名、対数の表記法、利用される分野を以下の表に記す。各分野においては、表記されている対数の底数が自明の場合、 $log x$ などと底を省略して表記する。「ISO表記」列には、国際標準化機構（ISO）の提案する表記（ISO 80000-2）を掲載する。 $log x$ 表記は下記の一般的な対数全てにおいて、もしくは底数があまり意味を持たない時において使われ得る表記であるため、実際の底の値がいくつなのかは、表記される文脈から推測する必要がある。 $log$ 表記は、計算機科学においては二進対数を、数学においては自然対数を^[6]、その他の分野においては常用対数を指していることが多い^[7] 。

底 $b$	対数名_b x	ISO表記	その他の表記	利用分野
2	二進対数	$lb x$ ^[8]	$ld x$ , $log x$ , $lg x$ ,^[9] $log 2 x$	計算機科学、情報理論、バイオインフォマティクス、音楽理論、撮影
$e$	自然対数	$ln x$ ^{[注 3]}	$log x$ (数学^[13]、プログラミング言語^{[注 4]}）、 $log e x$	数学、物理学、化学統計学、経済学、情報理論、工学
10	常用対数	$lg x$	$log x$ , $log 10 x$ （工学、生物学、天文学）	工学関連の様々な分野対数表、携帯電卓、分光法
$b$	$b$ を底とする対数	$log b x$		数学

歴史[編集]

詳細は「対数の歴史（英語版）」を参照

17世紀ヨーロッパにおける対数の発見は、数学の範囲を代数学的手法によるものから解析学の領域へと拡張させることとなった。対数の概念は、1614年にジョン・ネイピアによって『Mirifici Logarithmorum Canonis Descriptio』という書籍の中で初めて公式に提唱された^[14]^[15]。このネイピアの発見以前にも、プロスタファエレシス（英語版）や数列表など同様のタイプの数学的技法がヨスト・ビュルギによって1600年前後に発明されていた^[16]。対数を意味する「logarithm」の語は中世ラテン語から来ており、「比率、言葉」などの意味がある「logos」と「数」の意である「arythmos」との合成語である。

ある数の常用対数とは、その数を得るのに必要な10の累乗の指数のことである^[17]。アルキメデスが「数の順序」と呼んだ、書くのに非常に多くの数字を要する数についての言及は、常用関数に関する大雑把な言及である^[18]。対数に実質的に関連している最初の概念は、プロスタファエレシスと呼ばれる、乗算を加算に変換する発見的な手法であり、これらの中には三角恒等式から導かれた数表を用いて計算するものもあった^[19]。

今日自然対数として知られている対数関数の発明は、当時プラハに住んでいたベルギーのイエズス会士グレゴリー・デ・セント＝ビンセント（英語版）による直角双曲線の求積の試みをきっかけとするものだった。アルキメデスは紀元前3世紀に放物線の求積法を発見していたが、双曲線の求積は、セント＝ビンセントが1647年に解を公表するまで、誰も取り組んできていなかった。同じくイエズス会士だったアルフォンス・デ・サラサ（英語版）は、対数関数がその独立変数による等比数列と関数の値による等差数列との間に与える関係性から、セント＝ビンセントによる求積法とプロスタファエレシスとを結びつけ、新たに「双曲線対数」すなわち今日の自然対数という用語を生み出した。これらの概念は、クリスティアーン・ホイヘンスやジェームス・グレゴリーらによってすぐに高い評価を受けることとなった。 $log y$ の表記はゴットフリート・ライプニッツによって1675年に採用され、翌年には積分記号 ${\textstyle \int {\frac {dy}{y}}}$ と関連付けられた^[20]。

オイラーが現代的な複素自然対数の概念を提唱する前の1714年に、ロジャー・コーツも以下の式を得てほぼ同等の結果を示していた^[21]。

\log(\cos \theta +i\sin \theta )=i\theta .

脚注[編集]

[脚注の使い方]

注釈[編集]

^ 対数法則を解説した文献は左記の他にも多数存在する。
^ 底の変換公式は、対数の定義式 ${\textstyle x=b^{\log _{b}x}}$ について、 $k$ を底として両辺の対数をとり、 $\log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b.$ と変形させることにより導かれる。
^ 一部の数学者はこの記法を不可としている。ポール・ハルモスは1985年の自伝の中で、ln表記は子供じみており、数学者は今まで誰も使ったことがないと批判している^[10]。この表記は19世紀から20世紀の数学者アービング・ストリンガム（英語版）によって考案されたものである^[11]^[12]。
^ 例えば、C言語、Java。Haskell、BASICなど。

出典[編集]

^ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8 ^{[リンク切れ]}, chapter 1
^ Shailesh Shirali 2002, section 4, (Douglas Downing 2003, p. 275), or Kate & Bhapkar 2009, p. 1-1
^ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5 , p. 21
^ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-9 , chapter 17, p. 275
^ Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, p. 228, ISBN 978-0-240-52037-7
^ Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, p. 23, "One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base $b$ of the logarithm when $b = 2$ ."
^ Parkhurst, David F. (2007), Introduction to Applied Mathematics for Environmental Science (illustrated ed.), Springer Science & Business Media, p. 288, ISBN 978-0-387-34228-3
^ Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
^ See footnote 1 in Perl, Yehoshua; Reingold, Edward M. (December 1977), “Understanding the complexity of interpolation search”, Information Processing Letters 6 (6): 219–22, doi:10.1016/0020-0190(77)90072-2
^ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4
^ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. xiii
^ Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, p. 59, ISBN 978-0-12-370478-8
^ See Theorem 3.29 in Rudin, Walter (1984), Principles of mathematical analysis (3rd ed., International student ed.), Auckland: McGraw-Hill International, ISBN 978-0-07-085613-4
^ Napier, John (1614) (ラテン語), Mirifici Logarithmorum Canonis Descriptio [The Description of the Wonderful Canon of Logarithms], Edinburgh, Scotland: Andrew Hart
The sequel ... Constructio was published posthumously:
Napier, John (1619) (ラテン語), Mirifici Logarithmorum Canonis Constructio [The Construction of the Wonderful Rule of Logarithms], Edinburgh: Andrew Hart
Ian Bruce has made an annotated translation of both books (2012), available from 17centurymaths.com.
^ Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
^ Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), “Jost Bürgi's method for calculating sines”, Historia Mathematica 43 (2): 133–147, arXiv:1510.03180, doi:10.1016/j.hm.2016.03.001, MR3489006
^ William Gardner (1742) Tables of Logarithms
^ Pierce, R. C. Jr. (January 1977), “A brief history of logarithms”, The Two-Year College Mathematics Journal 8 (1): 22–26, doi:10.2307/3026878, JSTOR 3026878, https://jstor.org/stable/3026878
^ Enrique Gonzales-Velasco (2011) Journey through Mathematics – Creative Episodes in its History, §2.4 Hyperbolic logarithms, p. 117, Springer ISBN 978-0-387-92153-2
^ Florian Cajori (1913) "History of the exponential and logarithm concepts", American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.
^ Stillwell, J. (2010), Mathematics and Its History (3rd ed.), Springer

[3] 対数法則を解説した文献は左記の他にも多数存在する。

[4] 底の変換公式は、対数の定義式 ${\textstyle x=b^{\log _{b}x}}$ について、 $k$ を底として両辺の対数をとり、 $\log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b.$ と変形させることにより導かれる。

[15] 一部の数学者はこの記法を不可としている。ポール・ハルモスは1985年の自伝の中で、ln表記は子供じみており、数学者は今まで誰も使ったことがないと批判している^[10]。この表記は19世紀から20世紀の数学者アービング・ストリンガム（英語版）によって考案されたものである^[11]^[12]。

[17] 例えば、C言語、Java。Haskell、BASICなど。

[1] Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8 ^{[リンク切れ]}, chapter 1

[2] Shailesh Shirali 2002, section 4, (Douglas Downing 2003, p. 275), or Kate & Bhapkar 2009, p. 1-1

[5] Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5 , p. 21

[6] Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-9 , chapter 17, p. 275

[7] Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, p. 228, ISBN 978-0-240-52037-7

[8] Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, p. 23, "One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base $b$ of the logarithm when $b = 2$ ."

[9] Parkhurst, David F. (2007), Introduction to Applied Mathematics for Environmental Science (illustrated ed.), Springer Science & Business Media, p. 288, ISBN 978-0-387-34228-3

[gullberg-10] Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9

[11] See footnote 1 in Perl, Yehoshua; Reingold, Edward M. (December 1977), “Understanding the complexity of interpolation search”, Information Processing Letters 6 (6): 219–22, doi:10.1016/0020-0190(77)90072-2

[12] Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4

[13] Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. xiii

[14] Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, p. 59, ISBN 978-0-12-370478-8

[16] See Theorem 3.29 in Rudin, Walter (1984), Principles of mathematical analysis (3rd ed., International student ed.), Auckland: McGraw-Hill International, ISBN 978-0-07-085613-4

[18] Napier, John (1614) (ラテン語), Mirifici Logarithmorum Canonis Descriptio [The Description of the Wonderful Canon of Logarithms], Edinburgh, Scotland: Andrew Hart
The sequel ... Constructio was published posthumously:
Napier, John (1619) (ラテン語), Mirifici Logarithmorum Canonis Constructio [The Construction of the Wonderful Rule of Logarithms], Edinburgh: Andrew Hart
Ian Bruce has made an annotated translation of both books (2012), available from 17centurymaths.com.

[19] Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press

[folkerts-20] Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), “Jost Bürgi's method for calculating sines”, Historia Mathematica 43 (2): 133–147, arXiv:1510.03180, doi:10.1016/j.hm.2016.03.001, MR3489006

[21] William Gardner (1742) Tables of Logarithms

[22] Pierce, R. C. Jr. (January 1977), “A brief history of logarithms”, The Two-Year College Mathematics Journal 8 (1): 22–26, doi:10.2307/3026878, JSTOR 3026878, https://jstor.org/stable/3026878

[23] Enrique Gonzales-Velasco (2011) Journey through Mathematics – Creative Episodes in its History, §2.4 Hyperbolic logarithms, p. 117, Springer ISBN 978-0-387-92153-2

[24] Florian Cajori (1913) "History of the exponential and logarithm concepts", American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.

[25] Stillwell, J. (2010), Mathematics and Its History (3rd ed.), Springer

[1]

[2]

[注 1]

[注 2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[注 3]

[13]

[注 4]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[10]

[11]

[12]

演算の結果
加法 (+)
$項 + 項 = 和$ $加法因子 + 加法因子 = 和$ $被加数 + 加数 = 和$
減法 (-)
$被減数 - 減数 = 差$
乗法 (×)
$因数 \times 因数 = 積$ $被乗数 \times 乗数 = 積$ $被乗数 \times 倍率 = 積$
除法 (÷)
$被除数 \div 除数 = 商$ $被約数 \div 約数 = 商$ $実 \div 法 = 商$ $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}分子/分母 = 商$
剰余算 (mod)
$被除数 .mw-parser-output .monospaced{font-family:monospace,monospace} mod 除数 = 剰余$ $被除数 mod 法 = 剰余$
冪 (^)
$底冪指数 = 冪$
冪根 (√)
$次数 \sqrt 被開方数 = 冪根$
対数 (log)
$log 底 (真数) = 対数$
表話編歴